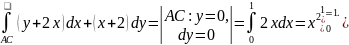Кратные интегралы Повторный интеграл

Задача 11. Вычислить повторный интеграл:

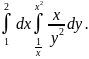
Решение. Сначала вычисляется внутренний интеграл, где у является переменной, а х постоянной:

Полученный результат подставить под знак внешнего интеграла и проинтегрировать его по переменной х.

Таким образом,

Двойной интеграл

Задача 12. Привести двойной интеграл

по области D к повторному двумя способами и вычислить его.

Решение. Вычисление двойного интеграла начинается с изображения области интегрирования. Все линии, ограничивающие область, необходимо построить и подписать (рис.3).

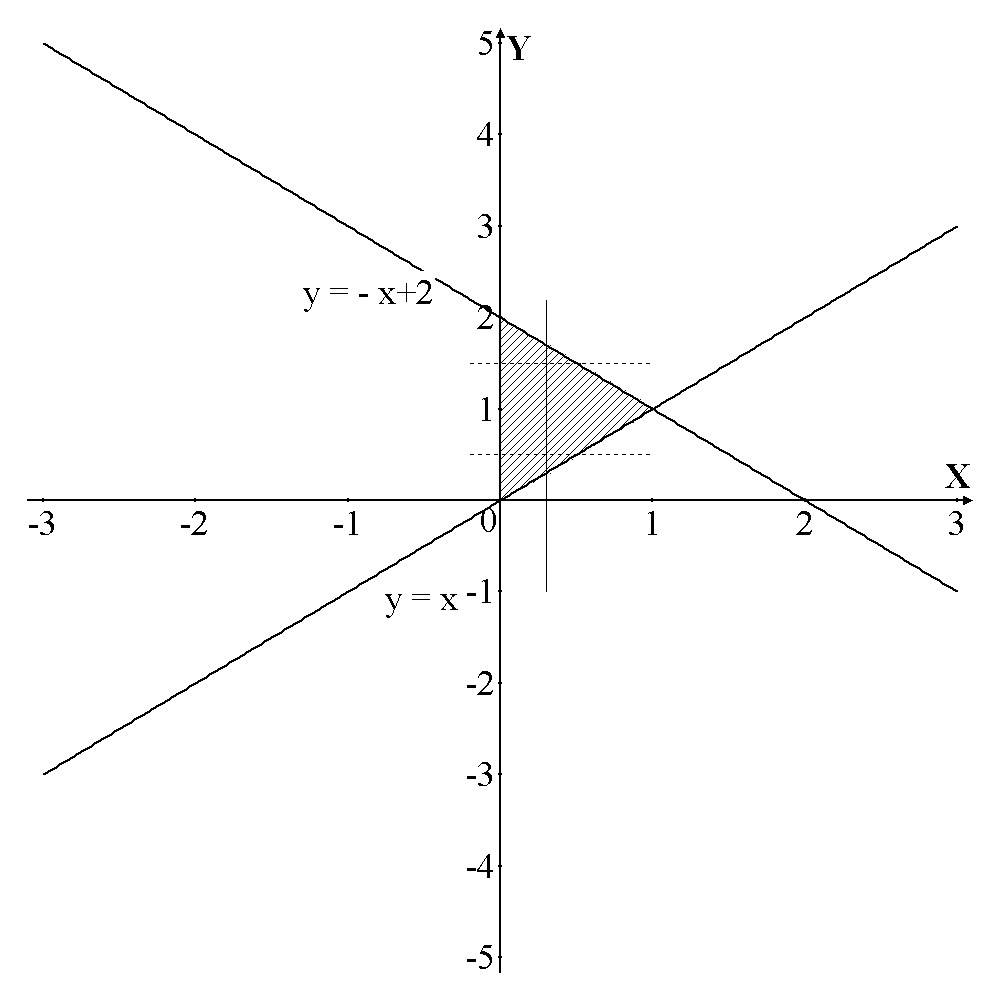
Рис. 3

Следующий шаг – переход от двойного интеграла к повторному. Для этого необходимо выбрать порядок интегрирования в повторном интеграле, т.е. 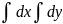или .

Чтобы выбрать наиболее удобный для вычисления порядок интегрирования, надо посмотреть, относительно какой оси нет «узлов» (то есть точек стыка различных линий). В нашем случае относительно оси Ох нет «узлов», поэтому в таком порядке как будет один повторный интеграл.

Для того чтобы найти внешние пределы интегрирования, нужно спроецировать крайние точки области на ось, дифференциал которой стоит под знаком внешнего интеграла. В нашем случае ─ на ось Ох, т.к. имеет место . Получим

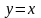Внутренние пределы показывают, как изменяется у. Для их определения внутри отрезка [0; 1] провести стрелку параллельно оси Оу и ответить на вопрос чему равен у на линии входа и линии выхода (в данном случае вход на линии , выход на линии ). Таким образом,

1. Сначала вычисляется внутренний интеграл, где y является переменной, а х постоянной:

2. Затем вычисляется внешний интеграл, подставив в него результат вычисления внутреннего интеграла.

При расстановке пределов вторым способом получается следующий результат

Геометрические приложения двойного интеграла

Задача 13. Пользуясь двойным интегралом, найти площадь плоской области D, ограниченной указанными линиями:

Решение. Площадь с помощью двойного интеграла вычисляется по формуле

Начать следует с изображения области, площадь которой требуется найти. На рис.4

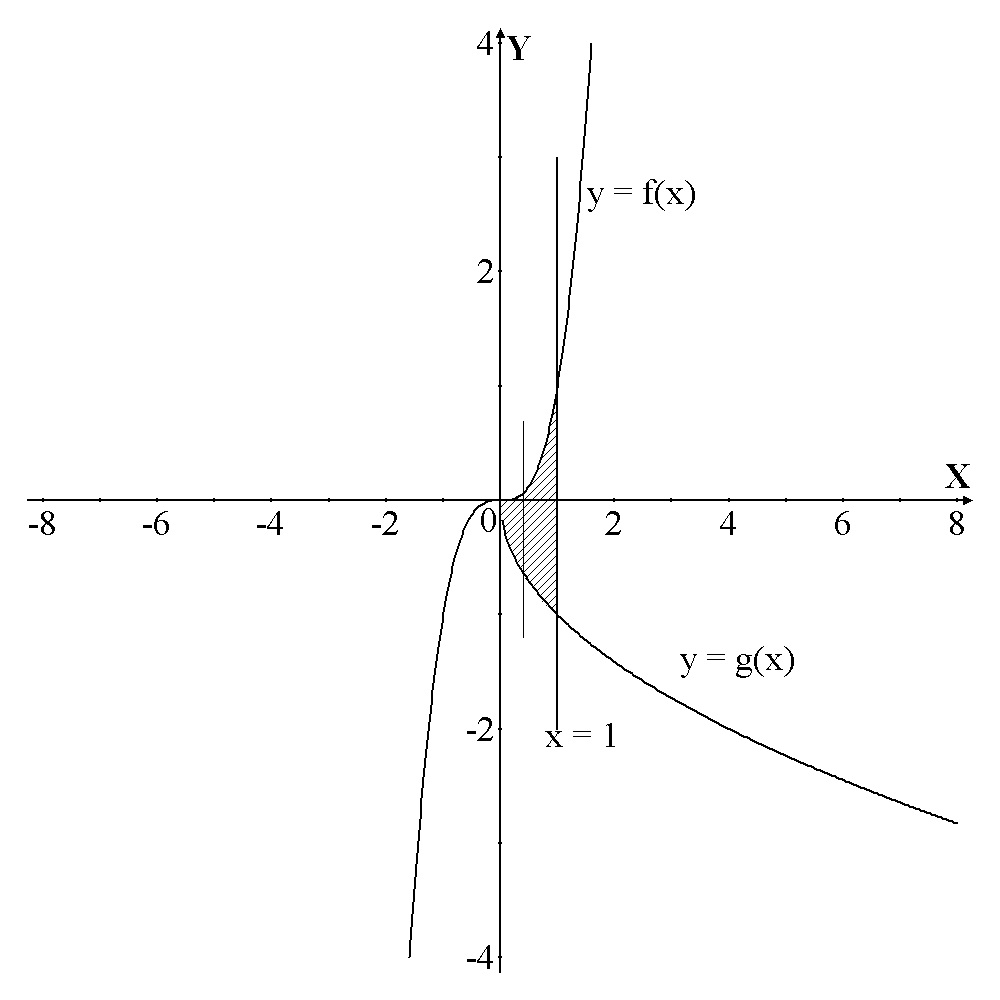
Рис. 4

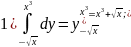
Криволинейный интеграл Криволинейный интеграл по координатам

Задача 14. Вычислить криволинейный интеграл

1) L: отрезок прямой от т.А(0;0) до т.В(1;2);

2) L: дуга параболы от т.А(2;1) до т.В(8;2);

3) L: ломаная АСВ, где А(0;0), С(1;0), В(1;2).

Решение. Для вычисления криволинейного интеграла по координатам надо с помощью заданного пути интегрирования преобразовать криволинейный интеграл в определенный интеграл. Пределы интегрирования зависят от того к какой переменной осуществляется переход под знаком интеграла.

в ) В данном случае путь интегрирования – ломаная АСВ, где А(0;0), С(1;0), В(1;2) (рис.5).

Рис. 5

Ломаная АСВ состоит из двух звеньев АС и СВ. Поэтому исходный интеграл по ломаной АСВ следует разбить на сумму двух интегралов по путям АС и СВ.