Введение

Цель преподавания математики – ознакомить курсанта (студента) с основами математического аппарата, необходимого для решения теоретических и практических задач, привить курсантам (студентам) умение самостоятельно изучать учебную литературу по математике и её приложениям, развить логическое мышление и повысить общий уровень математической культуры. В достижении этой цели помогают типовые расчеты (ТР).

Данное пособие содержит типовой расчет по интегральному исчислению функции одной и нескольких переменных и предназначен для курсантов первого курса. Типовой расчет содержит теоретические вопросы, которые являются общими для всех курсантов, и расчетные задачи – индивидуальные для каждого курсанта. Всего предлагается 30 различных вариантов задач. Помимо перечисленных пунктов пособие содержит решение типового варианта.

Выполнение курсантами (студентами) ТР контролируется преподавателем. Задачи сдаются курсантами на проверку в письменном виде. Завершающим этапом является защита ТР. Во время защиты курсант должен уметь правильно отвечать на теоретические вопросы, пояснять решения задачи, решать задачи аналогичного типа.

Контролные вопросы

1. Первообразная функции на множестве .

2. Неопределенный интеграл.

3. Геометрический смысл неопределенного интеграла.

4. Свойства неопределенного интеграла.

5. Закончить формулы:

…

…

…

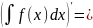6. Укажите одну из первообразных функции .

7. Формула интегрирования по частям в неопределенном интеграле.

8. Геометрический и физический смысл определенного интеграла.

9. Формула Ньютона-Лейбница.

10. Отличие метода замены переменной в неопределенном и определенном интеграле.

11. Формула интегрирования по частям в определенном интеграле.

12. Несобственные интегралы первого и второго рода.

13. Двойной интеграл.

14. Геометрический и физический смысл двойного интеграла.

15. Криволинейный интеграл 1 и 2 рода.

Решение типового варианта Табличное интегрирование

Задача 1. Найти интегралы:

Решение. 1) Для нахождения данного интеграла сначала осуществить почленное деление числителя на знаменатель в подынтегральной функции, выполнить действия со степенями, применяя формулы

и далее использовать формулу интеграла от степенной функции

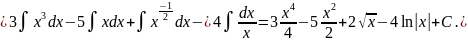
2), 3), 4) Для нахождения данных интегралов используется формула

Метод замены переменной в неопределенном интеграле

Задача 2. Найти неопределенные интегралы:

Решение. Для нахождения данных интегралов используется либо метод замены переменной, либо подведение под знак дифференциала. Для этого подынтегральное выражение нужно разбить на два множителя так, чтобы были видны некоторая функция и ее производная (или почти её производная). Тогда функцию обозначить новой переменной, затем продифференцировать полученное равенство и осуществить замену. В результате подстановки получается табличный интеграл, после нахождения которого необходимо сделать обратную замену.

или воспользоваться формулой , тогда