Основы линейной алгебры.

1.Правило Крамера для системы 2х линейных уравнений.

(*)

_

(

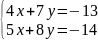
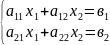
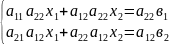
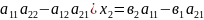
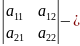∆= главный определитель

∆=

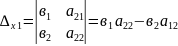
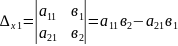
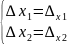
Правило Крамера для системы линейных уравнений

1.∆≠0 то система (*) имеет 1решение,которое находится по формулам:

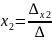
2.∆=0, а хотя бы один из вспомогательных определителей система (*) не имеет решений.

3.∆=0 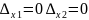, то система (*) имеет бесконечное число решений.

Пример1.

∆=32-35=-3≠0

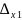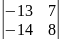= = -104+98=-6 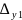= =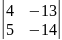-56+65=9

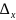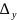х= /∆=2 у= /∆=-3

пример2.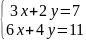 ∆= =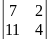12-12=0 =28-22=6≠0 нет решений.

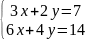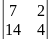Пример3. ∆= =0 =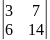 =0 = =0 ∆=

У=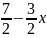 ответ:

2.Определители

1.Определителем 2порядка называется число, опр по формуле ∆= =

2.Определителем 3порядка наз. Число, опр по формуле ∆=

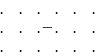= правило Сарруса (правило треуг.)

3.Определителем n-ого порядка наз ∆ определяемый с помощью табл.∆= (**)

3.Свойства определителей.

Транспонирование – определитель (**) наз. Такое его преобразование, при кот. Его строки становятся столбцами с теми же самыми номерами.

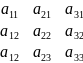Св-во1.Определитель не меняется при транспонировании

Пример1.∆= ∆=

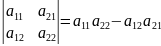
Св-во2.Если какая-нибудь строка определителя состоит из одних нулей, то его значение=0

Св-во3.При перестановке местами любых 2х строк определитель меняет знак.

Пример. =20+100-16-70=34 =16+70-20-100=-34 =16+70-20-100=-34

Св-во4.Определитель, сод. 2одинаковые строки = 0 =ав-ав=0

Св-во5.Общий множитель всех элементов строки можно выносить за знак определителя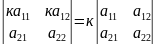

Св-во7.Если все элементы i-й строки определителя n-ого порядка представлены в виде суммы 2х слагаемых 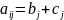=1,2,3…n ,то определитель равен сумме 2х определителей у которых все строки кроме такие же как в заданном определителе, а i–я трока в одном из слагаемых состоит из 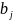,а в другом из элементов

= +

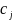
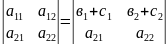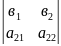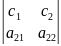
Св-во8.Если одна из строк определителя есть линейная комбинация его других строк, то определитель = 0 (следствие из св-ва7, св-ва6)

Св-во9.Определитель не меняется если к элементам одной из его строк +/- соответственные элементы др строки умноженные на одно и то же число.

= + =

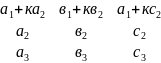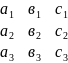4.Вычисление определителя, приведение к треугольному виду.

Св-во10.Если все элементы определителя расположенные по одну сторону от главной диагонали = 0, то этот определитель = произведению элементов, стоящих на главной диагонали.

Запись такого вида наз. Треугольным видом.

Прим.

5.Вычисление определителя методом Лапласа.

Опр1.Минором некоторого элемента с индексом n-ого порядка наз. Определитель n-1 порядка, полученного из исходного путем вычеркивания строки и столбца на пересечении которых находится выбранный элемент ( )

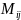Опр2. Алгебраическим дополнением элемента 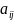определителя наз. Его минор взятый со знаком ( , где i-№ стороки, а j-№столбца( )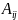

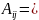
Прим.

Правило Лапласа для определителей.

∆= равен сумме произведений элементов некоторой строки(столбца) на их алгебраические дополнения по n-й строке

∆=

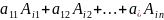
Прим.∆= =1( =35-12-2(15-8)+2(9-14)=-1

6.Правило Крамера для любой системы линейных уравнений.

(*) ∆=

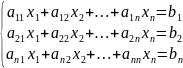Правило Крамера для любой системы линейных уравнений