§1.8.Коло змінного струму з послідовним з’єднанням r,l,c

Нехай маємо електричне коло.

З гідно 2 закону Кірхгофа для миттєвих значень маємо

Для комплексної форми напруг

Падіння напруги на елементах кола:

; ; ; тоді

Обозначимо - комплексний опір кола.

Маємо

- закон Ома для послідовного з’єднання r,L,C

Розглянемо комплексний опір .

, де

r – активний опір кола;

X_L – X_C = X – реактивний опір кола.

В показниковій формі запису комплексний опір

, де

- модуль комплексного опору;

- аргумент комплексного опору.

Нехай

- кут зсуву фаз між напругою та струмом.

Кут зсуву фаз між напругою та струмом в колі визначається тільки параметрами кола, величинами активного та реактивного опору, і залежить від початкової фази струму і напруги.

Приклад:

Д ано:

r = 50 Ом

X_L = 72 Ом

X_C = 22 Ом

Знайти: та побудувати векторну діаграму.

Найдемо падіння наруги на елементах кола

Побудуємо векторну діаграму.

По другому закона Кірхгофа маємо

Т аку діаграму називають променевою, так як вектори відкладають з однієї точки, початку координат.

Можна будувати векторну діаграму відкладаючи слідуючий вектор з кінця попереднього. Така діаграма носить назву топографічної.

§1.9.Трикутникі напруг та опорів

Р озглянемо послідовне з’єднання r,L,C.

Н ехай нам відомі . Побудуємо якісно векторну діаграму.

Обозначимо ,

- активна складова напруги;

- реактивна складова напруги.

В раховуючи обозначення побудуємо трикутник

Прямокутний трикутник, катетами якого є активна та реактивна напруги, а гіпотенуза напруга яку розглядають, називається трикутником напруг. Із трикутника напруг витікає:

Приклад. Маємо схему, в якій і .

Н еобхідно знайти

Я 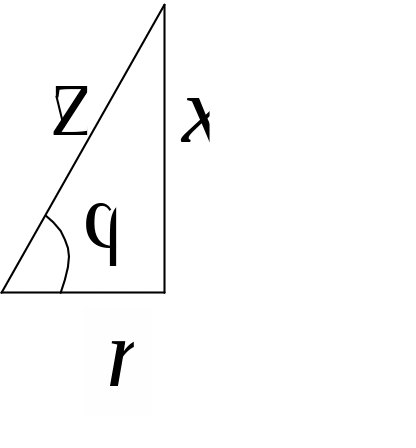кщо сторони трикутника розділити на одне і теж число, отримаємо подібний трикутник. Нехай цим числом буде струм, протікаючий в колі, тоді сторони трикутника будуть відповідати опорам кола.

; ;

Прямокутний трикутник, катетами якого є активний та реактивний опір, а гіпотенузою модуль опору кола, називають трикутником опорів.

, , ;

П риклад. Нехай задане коло в якому r = 30 Ом , Х_С = 30 Ом.

Знайти комплексний опір кола Z.

Ом

§1.10.Резонансні явища в колі з послідовним з’єднанням r,l,c

Р озглянемо послідовне з’єднання r,L,C. Таке коло називають послідовним коливальним контуром.

Комплексний опір такого кола .

Може виникнути ситуація, коли .

Резонансом називають такий режим пасивного кола, яке має катушки індуктивності та конденсатори, при якому його вхідний реактивний опір дорівнює нулю.

Умови резонансу для послідовного кола можна записати

, , , , .

Із ціх співвідношень видно, що режиму резонанса можна достигнути зміною кутової частоти, індуктивності або ємності.

Величини, які відносяться до режиму резонансу будемо відмічати індексом 0.

При постійних значеннях L,C резонансна кутова частота

При постійних резонансна індуктивність

При постійних резонансна ємність

П ри резонансі , напруги на індуктивності та ємності рівні між собою та протилежні по фазі. При резонансі коло, яке має катушки індуктивності та конденсатори, поводить себе як активний опір. Кут зсуву фаз між вхідним струмом та напругою дорівнює нулю. В момент резонансу модуль повного опору кола має мінімальне значення і при заданій вхідній напрузі струм має своє максимальне значення .

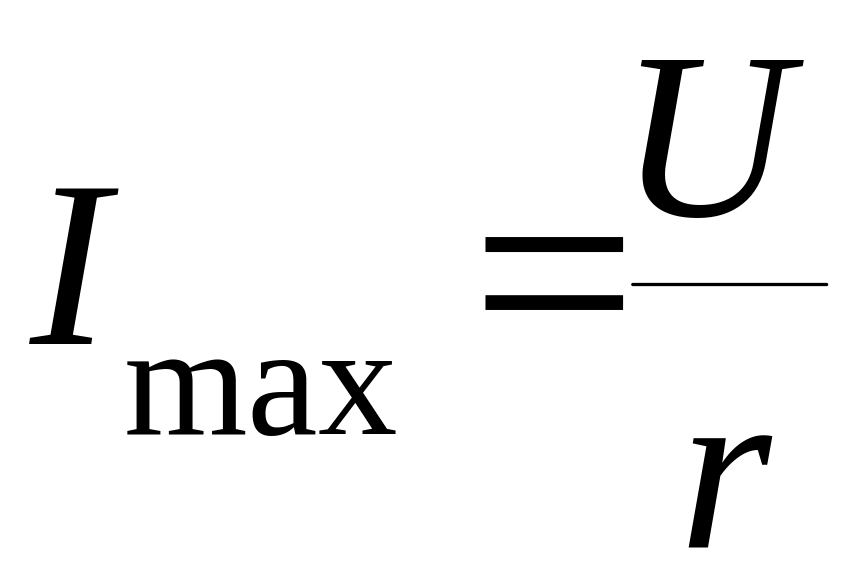При резонансі напруга на реактивних елементах може значно перевищувати напругу на вході кола, яка дорівнює падінню напруги на активному опору. Теоретично, при r = 0, в момент резонансу повний опір кола дорівнює нулю, а струм при конечному значенні напруги на вході нескінченно великий. Нескінченно великими будуть падіння напруги на індуктивності та ємності. Тому такий резонанс називають резонансом напруг.

Приклад. Задано послідовне коло r,L,C для якого r = 10 Ом, Х_L = 100 Ом, Х_С = 100 Ом. Напруга на вході . Знайти падіння напруг на елементах кола.

Так як , то в колі явище резонансу. Повний опір кола Z = r. Струм у колі

Отже, на реактивних елементах кола, діюче значення напруги в момент резонансу, значно перевищує напругу на вхідних затискачах. На практиці послідовне з’єднання L і С в силових колах не використовується, так як є ймовірність виникнення явища резонанса, а це може призвести до виходу із ладу обладнання.

При резонансі

- характеристичний або хвильовий опір кола.

Для характеристикі резонансних властивостей кола вводять поняття добротності коливального контуру.

Добротністю коливального контуру називають відношення напруги на реактивному елементі до напруги на вхідних затискачах схеми в момент резонансу.

Добротність контуру показує наскількі малі активні втрати енергії в електричному колі.