§1.6.Зображення електричних величин комплексними числами

Нехай задана напруга . Вектор зображаючий напругу можна записати

Множник показує, що вектор зображаючий напругу обертається з постійною кутовою швидкістю . Ця швидкість однакова для всіх векторів. Отже положення векторів відносно один одного не міняється. На основі цього їх можна вважати умовно нерухомими. Величину називють комплексною амплутудою напруги, - коиплексна амплітуда струму. Якщо комплексну амплітуду розділити на , то отримаємо комплексне діюче значення.

;

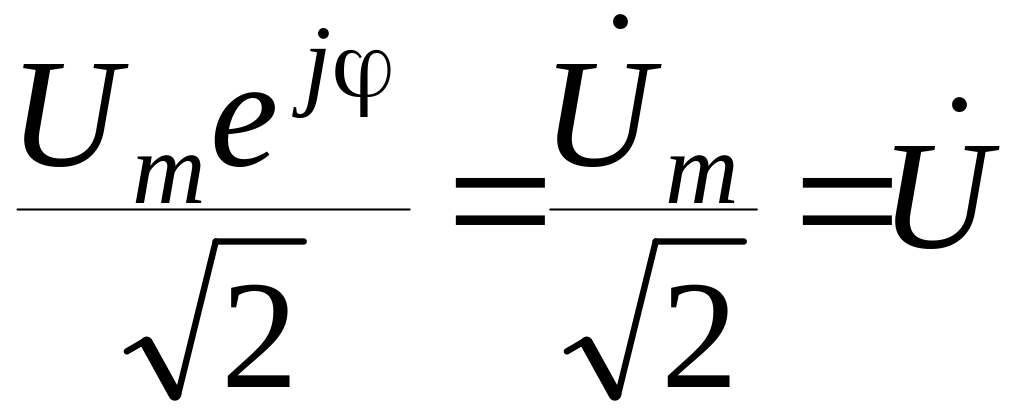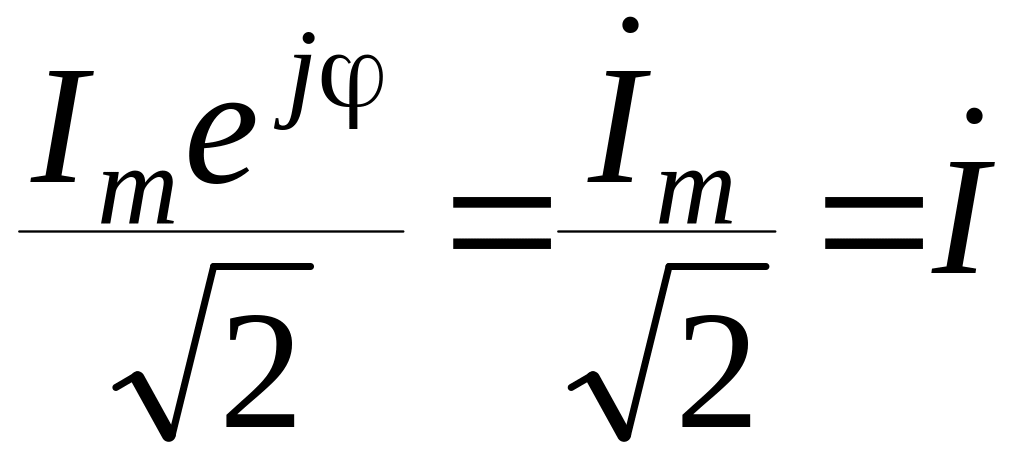
Перехід від миттєвих значень до комплексних діючих:

Нехай задано . Комплексна амплітуда

Комплексне значення

Зворотній перехід:

Задано

Миттєве значення напруги

§1.7.Розрахунок простих кіл змінного струму

Закон Ома для простих кіл змінного струму.

а) коло змінного струму з активним опором.

Нехай заданий активний опір, до якого прикладена напруга

Миттєве значення струму через опір дорівнює

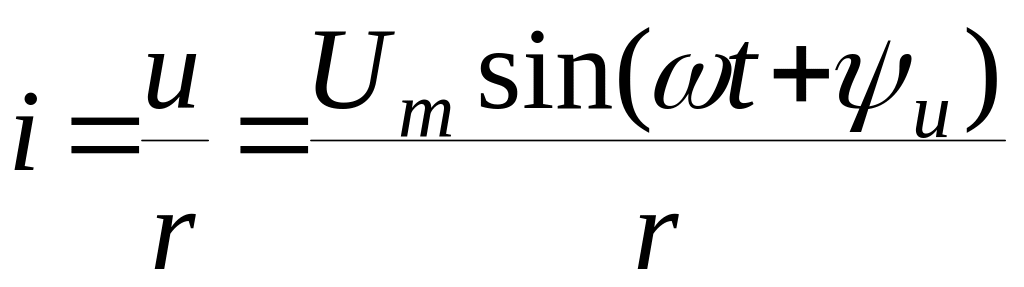
Обозначимо 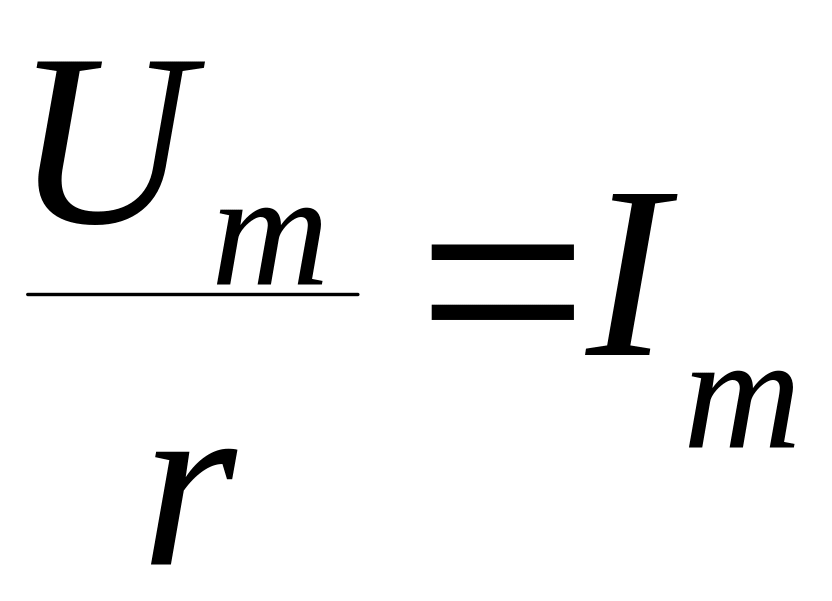, отримаємо

Таким чином струм співпадає по фазі з напругою.

Миттєве значення потужності р дорівнює

Миттєве значення потужності змінюєтьсяз подвійною кутовою частотою від 0 до 2UI.

Р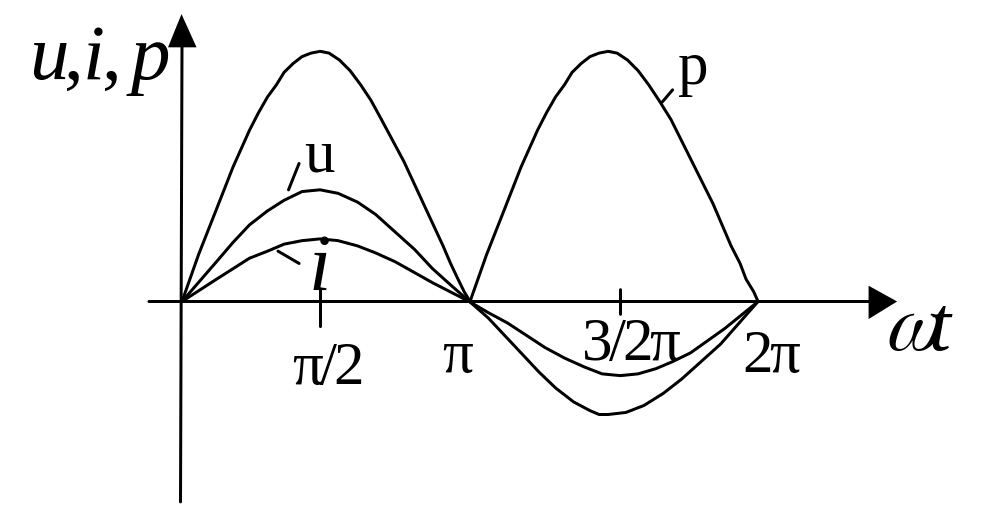 озглянемо графіки зміни струму, напруги та потужності на активному опорі.

Перейдемо від миттєвих значень до комплексних.

Нехай , тоді

Ц е закон Ома для активного опору в комплексній формі запису. На комплексній площині векторна діаграма має вигляд

Кут між та дорівнює 0.

б) коло змінного струму з індуктивністю.

Нехай маємо індуктивність, через яку протікає струм . Зміна струму в індуктивності визве появлення ЕРС самоіндукції. По закону Ленца вона протидіє зміні струму . отже при виборі однакового знаку та , знаки і завжди протилежні:

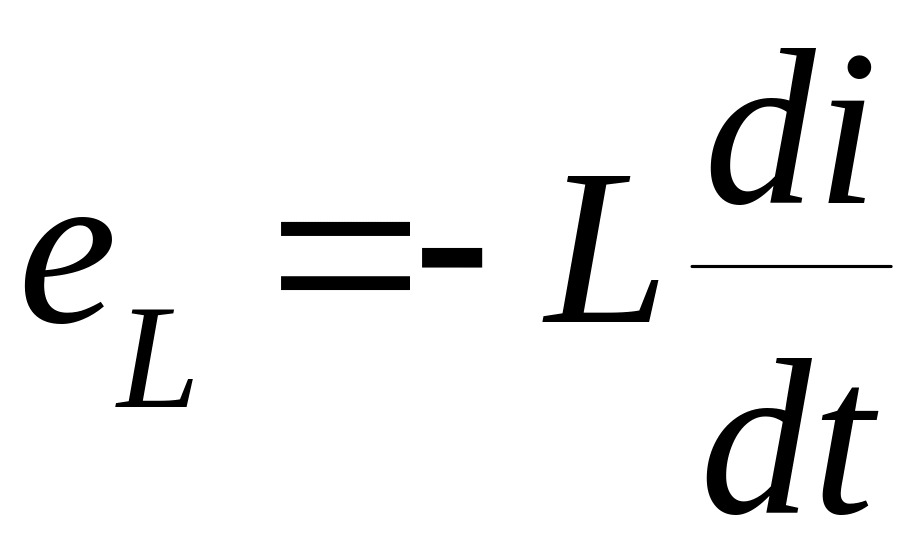
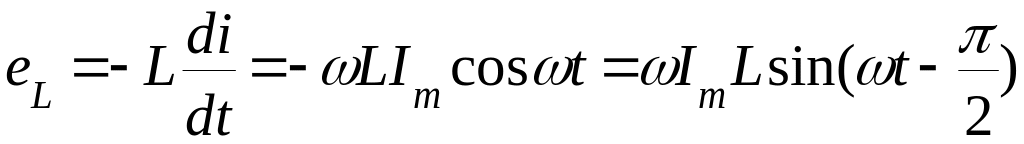
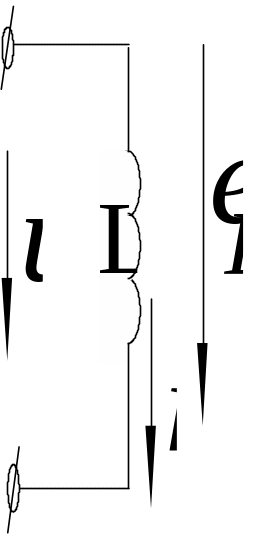
Обозначим і отримаємо

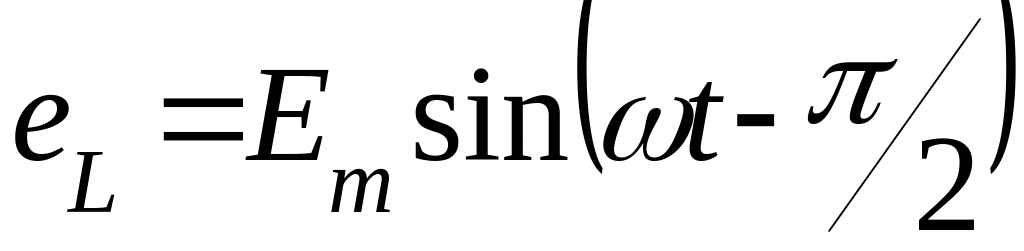
Таким чином, ЕРС відстає від струму на кут і відповідно вектор відстає від вектора . Для того, щоб через індуктивність протікав змінний струм до її клем необхідно прикласти напругу, яка дорівнює ЕРС самоіндукції і має протилежний напрямок. При однакових позитивних напрямках напруги та ЕРС вони будуть протилежні по знаку

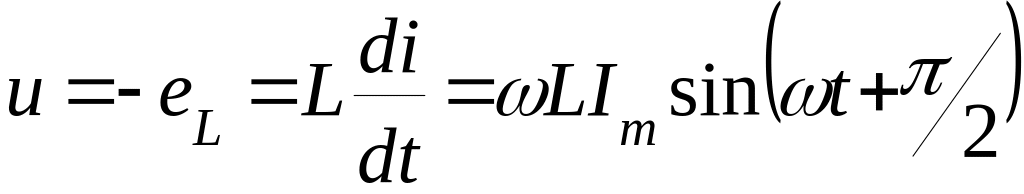
Обозначимо , тоді миттєве значення напруги

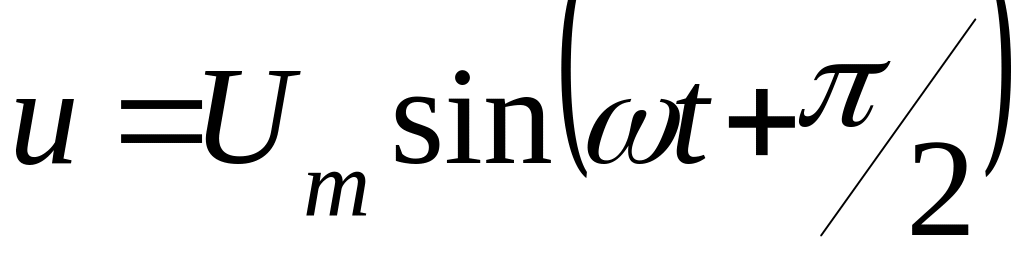
Напруга випереджує струм на кут .

Для діючих значень наруги та струму маємо співвідношення

;

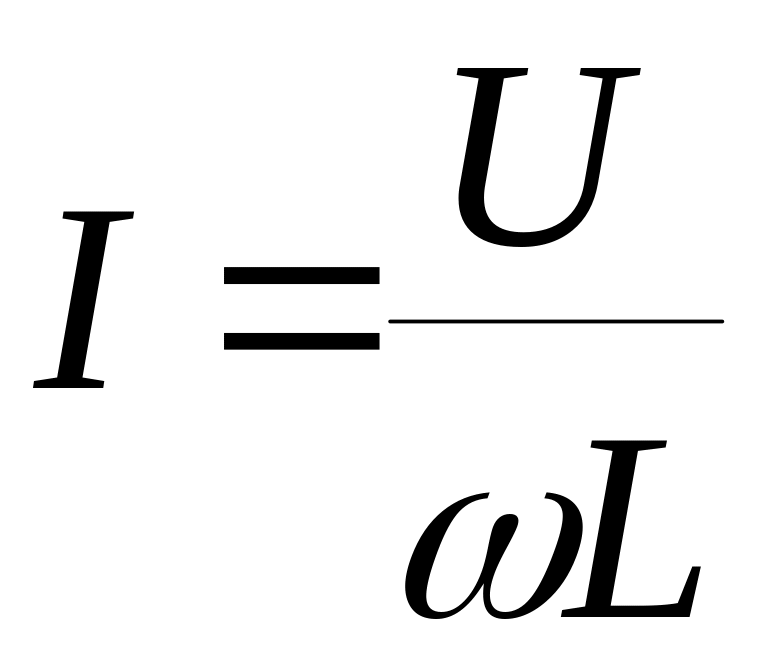
Величина має розмірність опору і називається індуктивним опором Х_L . Індуктивний опір лінійно залежить від частоти.

Миттєва потужність в індуктивності

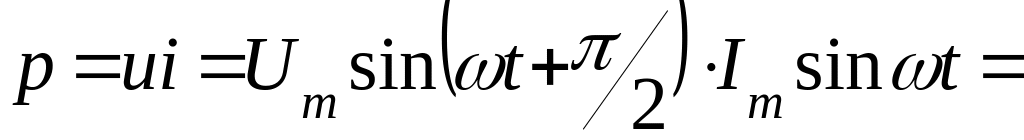
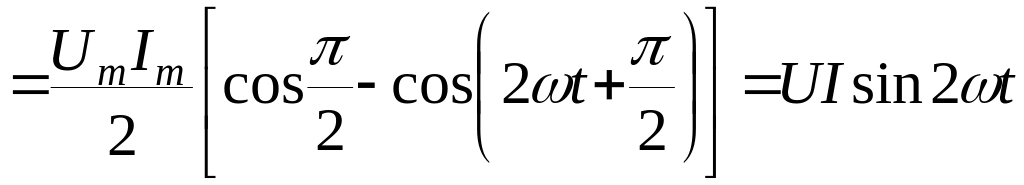
Миттєва потужність змінюється синусоідально з подвійною кутовою частотою, причому її середнє значення, або активна потужність р = 0.

Розглянемо графіки зміни .

Н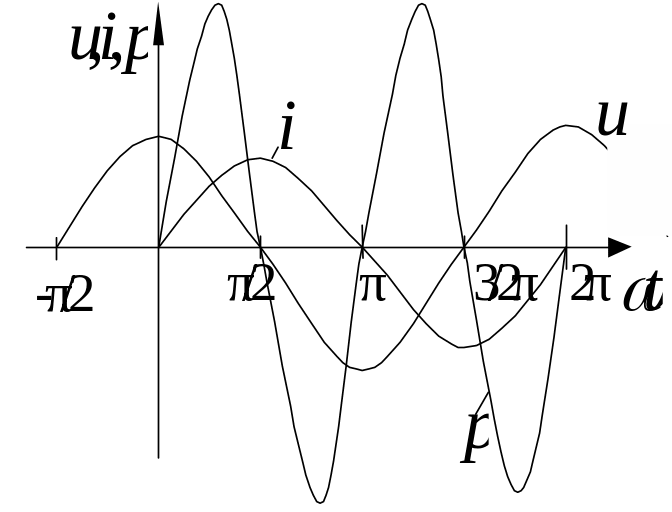 апруга на клемах індуктивності випереджує по фазі струм на кут , а вектор випереджує вектор на кут .

Перейдемо до комплексних величин

;

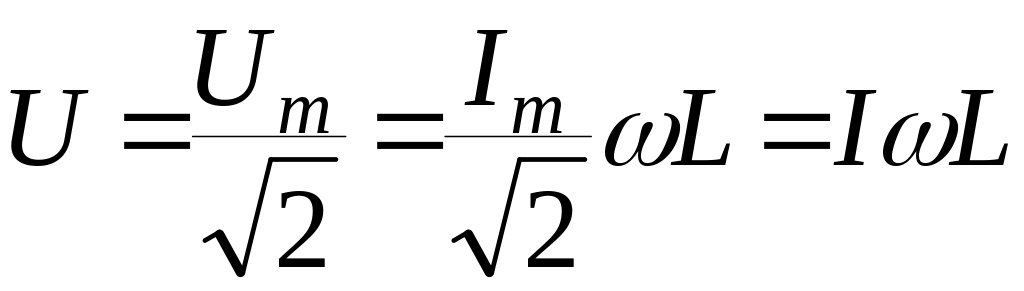- комплексний індуктивний опір.

- закон Ома для індуктивності.

В екторна діаграма має вигляд

в) коло змінного стуму з конденсатором.

Нехай маємо конденсатор, до якого прикладено напругу .

М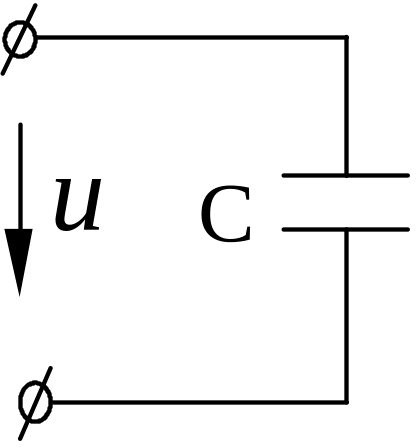 иттєва напруга дорівнює

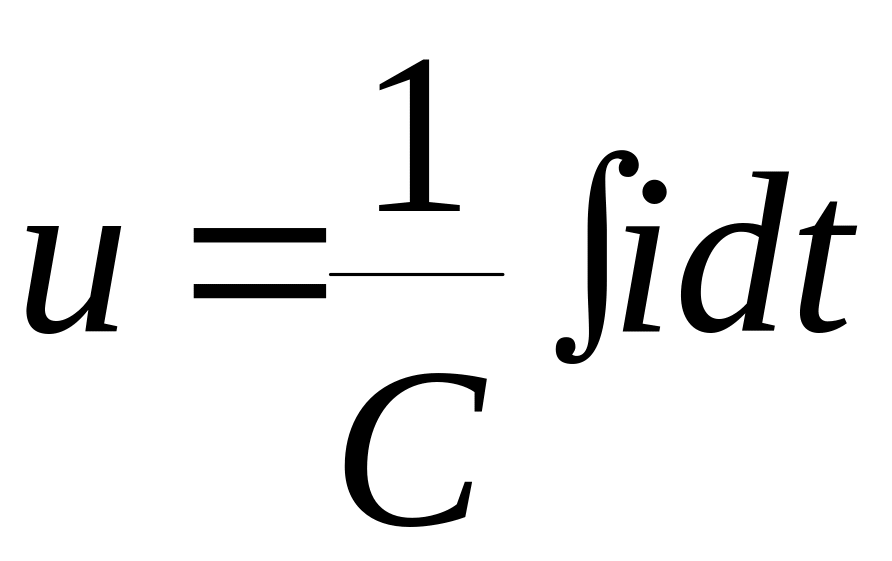
Якщо струм змінюється по закону , то будемо мати

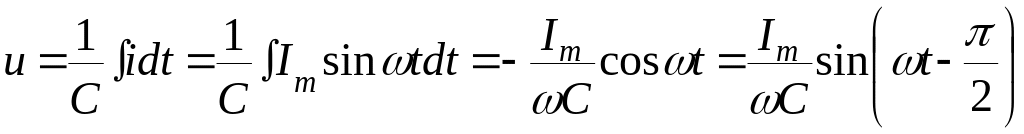
Якщо обозначимо 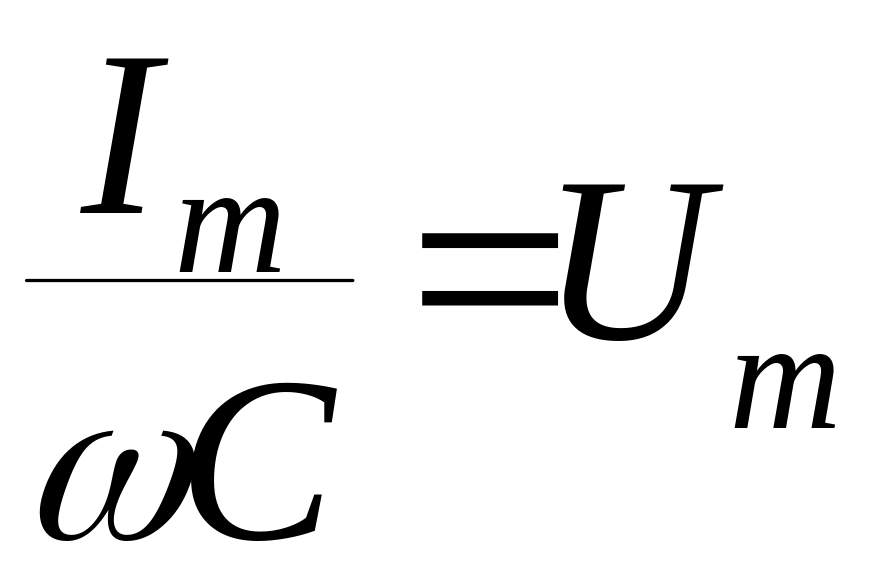матимемо .

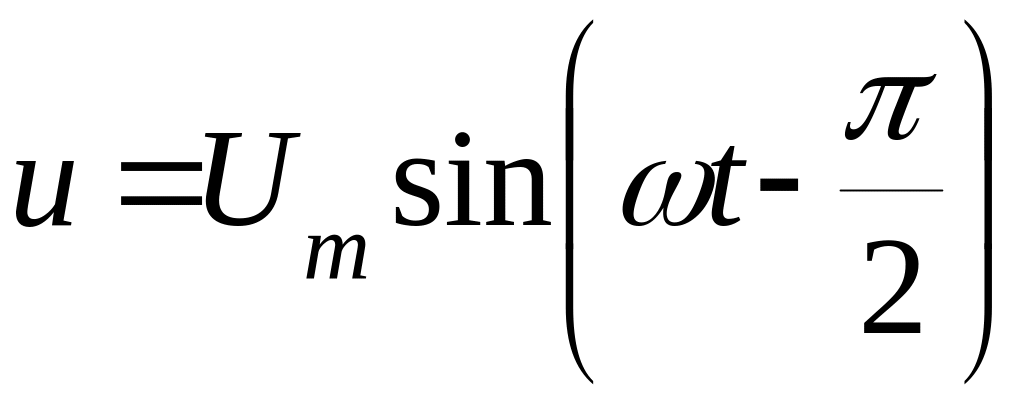Напруга на конденсаторі відстає від струму на кут . Величина 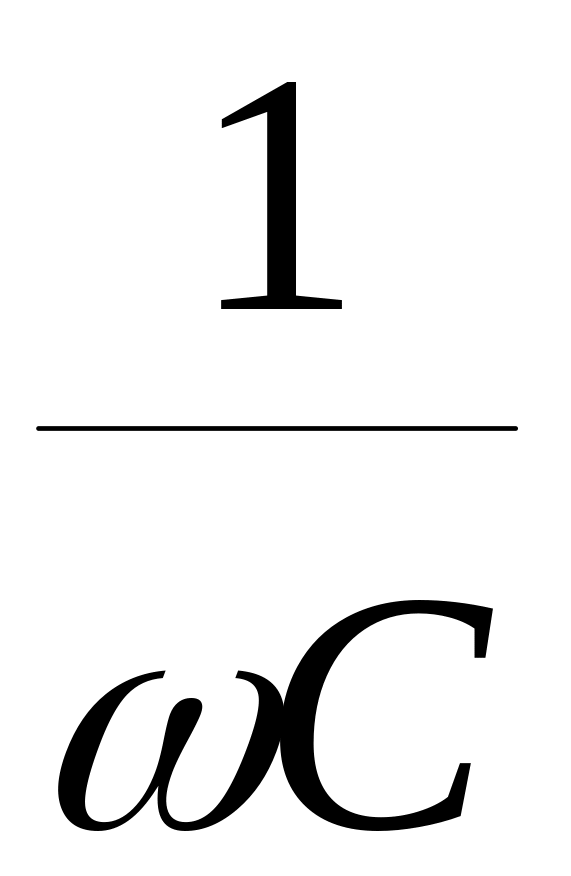має розмірність опору і називається ємкостним опором Х_С.

Миттєва потужність

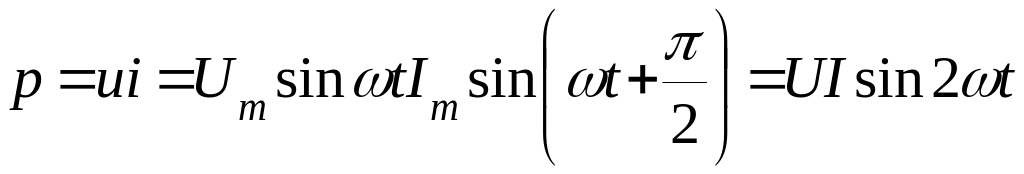
змінюється синусоідально з подвійною кутовою частотою і її середнє значення дорівнює 0.

Розглянемо графіки зміни .

П ерейдемо до комплексних величин.

Комплексний опір ємкості

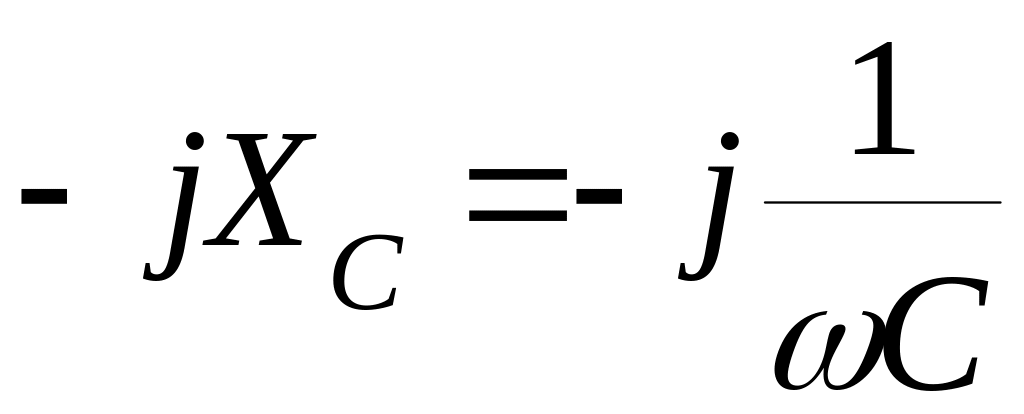
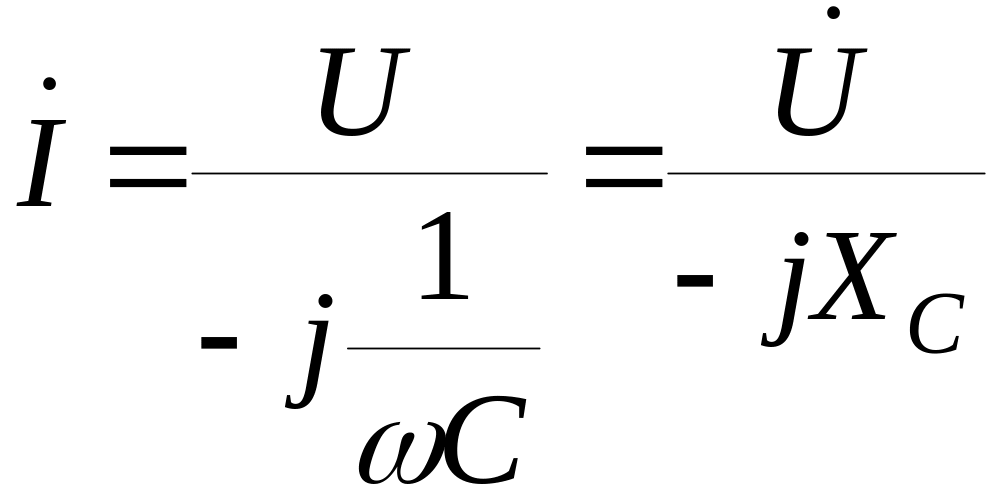- закон Ома в комплексній формі для ємкості.

Векторна діаграма.

На векторній діаграмі вектор напруги відстає від струму на кут

П ідведемо підсумок:

д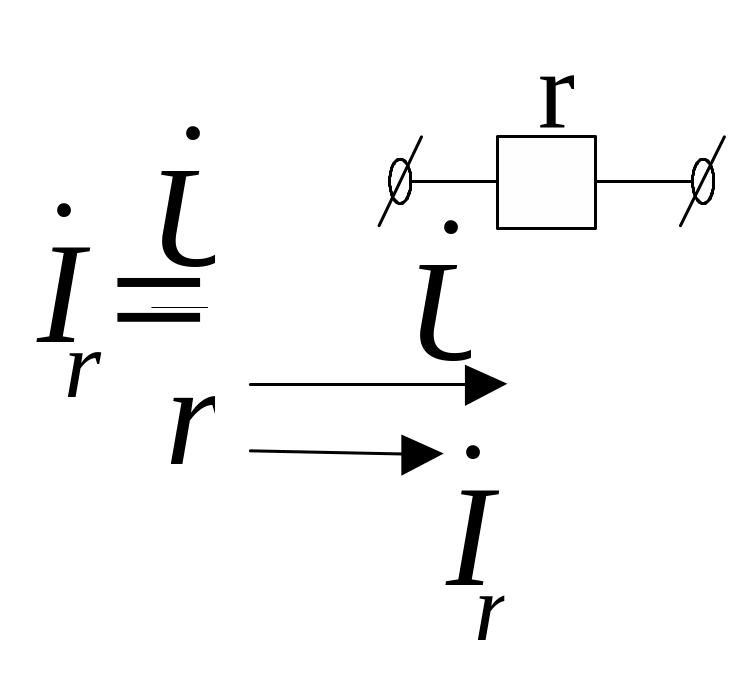 ля активного опору

д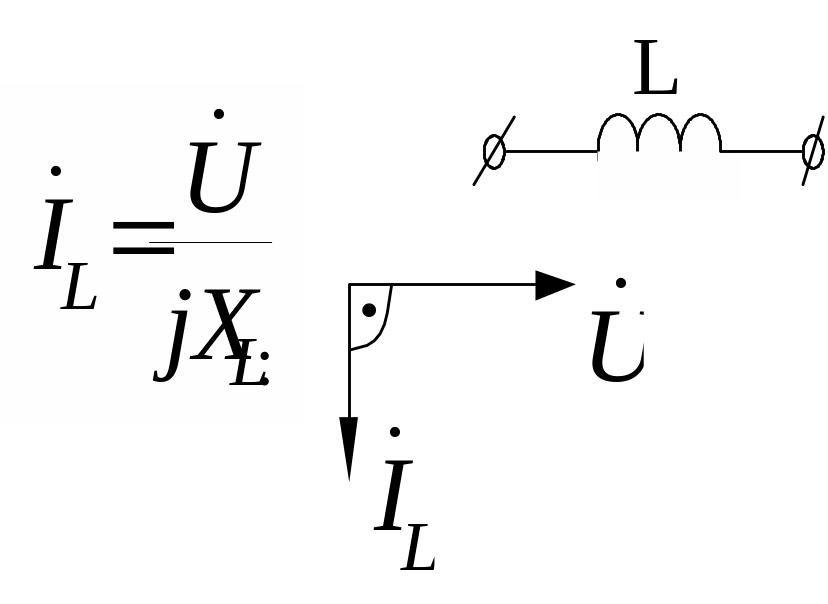 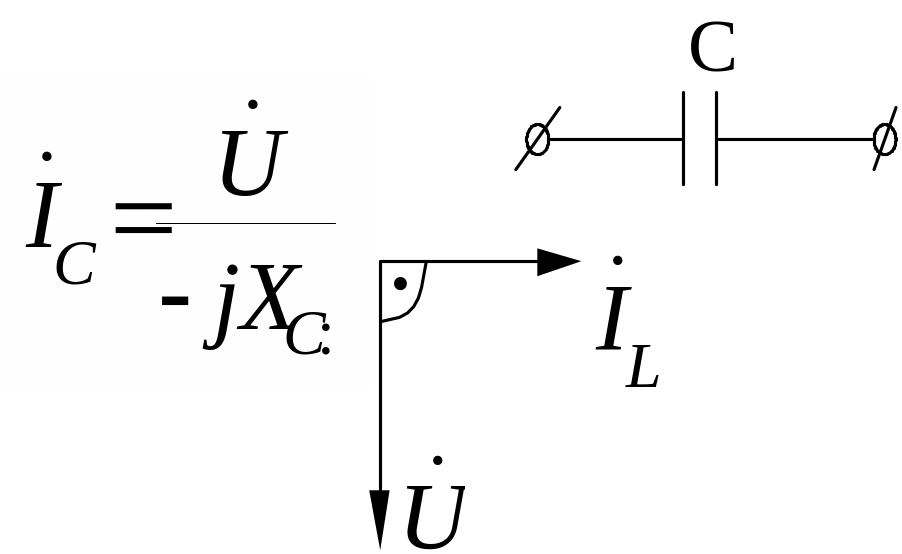ля індуктивності

для ємності