24.Экспоненциальная модель надежности по (модель Шумана).

Вводится ряд допущений и условий, основным из которых является условие существования программы исследователя системы. Остальные допущения и условия не связаны с какими-то специфическими свойствами ПО.

Условия сводятся к следующему:

1.Предполагается, что в начальный момент компоновки программных средств системы в них имеются небольшие ошибки (Е – количество ошибок). С этого времени отсчитывается время отладки тау, которое включает затраты времени на выявление ошибок с помощью тестов, на контрольные проверки и т.д. При этом время исправного функционирования системы не учитывается. В течение времени тау устанавливается эпсилон-нулевое(тау) ошибок в расчете на одну команду машинного языка. Т.о. удельное число ошибок на одну машинную команду остающихся в системе после времени тау работы равно

I – общее число машинных команд.

2.Предполагается, что значение функции частоты или интенсивности отказов z(t) пропорциональна числу ошибок, оставшихся в ПО после израсходования на отладку времени тау, то есть

C – коэффициент пропорциональности.

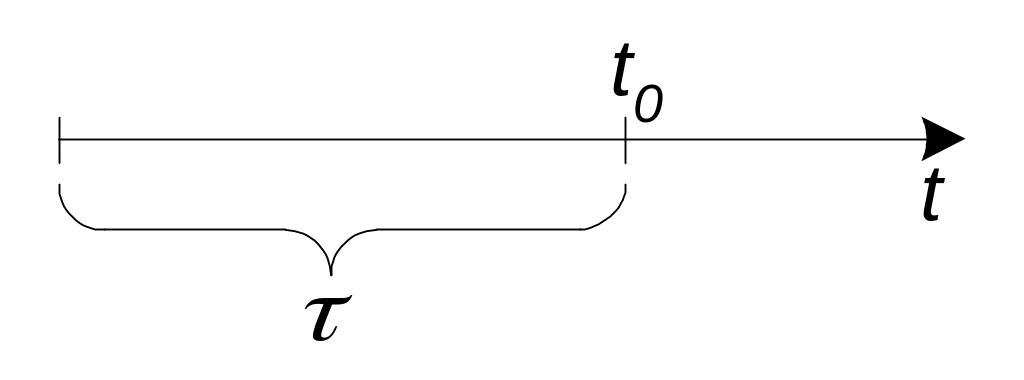
Тогда, если время работы системы t отсчитывается от момента времени t0, а тау остается фиксированным ( =const), то функция надежности или вероятность безотказной работы на интервале времени от 0 до t есть

Для нахождения С и Е используются принцип максимального правдоподобия (пропорция).

26.Статистическая модель Миллса

Эту модель можно использовать для сертификации программных средств.

В модели не используются предположения о поведении функции риска . Эта модель строится на твердом статистическом фундаменте.

Сначала программа «засоряется» некоторым количеством известных ошибок. Эти ошибки вносятся в программу случайным образом, а затем делается предположение, что для ее собственных и внесенных ошибок вероятность обнаружения одинакова и зависит только от их количества. Тестируя программу в течении некоторого времени и отсортировывая собственные и внесенные ошибки можно оценить N – первоначальное число ошибок в программе.

Предположим, что в программу было внесено S ошибок. Пусть при тестировании обнаружено (n+V) ошибок.

n – число собственных ошибок

V – число внесенных ошибок

Тогда оценка для N по методу максимального правдоподобия будет следующей

В действительности N можно оценивать после каждой ошибки. Миллс предлагает во время всего периода тестирования отмечать на графике число найденных ошибок и текущие оценки для N.

Вторая часть модели связана с выдвижением и проверкой гипотез о N.

Примем, что программе имеется не более k собственных ошибок и внесем в нее еще S ошибок. Теперь программа тестируется, пока не будут обнаружены все внесенные ошибки. Причем подсчитывается число обнаруженных собственных ошибок n. Уровень значимости С вычисляется по формуле

С – мера доверия к модели – вероятность того, что модель будет правильно отклонять ложные предположения.

Формулы для N и C образуют полезную модель ошибок.

Минусы модели

С нельзя предсказать до тех пор, пока не будут обнаружены все внесенные ошибки, это может не произойти до самого конца этапа тестирования.

Модификация формулы для С, если не все ошибки обнаружены:

j – найденные внесенные ошибки, j < S

Модель математически проста и интуитивно привлекательна. Легко представить программу внесения ошибок, которая случайным образом выбирает модуль и вносит логические ошибки, изменяя или убирая операторы. Природа внесения ошибок должна оставаться в тайне, но все их следует регистрировать с целью последующего деления на собственные и несобственные.