3.1 Вопросы для самопроверки

1. Что называется вектором?

2. Как найти проекции вектора, если известны координаты его начала и конца?

3. Что такое модуль вектора и как его найти?

4. Чему равно скалярное произведение векторов, заданных проекциями?

5. Как найти угол между векторами?

6. Чему равна площадь треугольника?

7. Чему равен объем пирамиды?

8. Напишите канонические уравнения прямой.

9. Как найти прямую, проходящую через две точки?

10. Как найти уравнение плоскости, проходящей через три точки?

11. Сформулируйте условие перпендикулярности прямой и плоскости.

3. Основные теоремы о пределах

Пределом функции в точке «а» называется постоянная величина «b», если для любого положительного сколь угодно малого >0 найдется такое положительное число >0, что для всех выполняется неравенство , что символически записывается так:

,

При вычислении пределов функций будем пользоваться следующими теоремами:

1. Предел алгебраической суммы функций равен алгебраической сумме их пределов.

2. Предел произведения функций равен произведению их пределов.

3. Постоянный множитель можно вынести за знак предела.

4. Предел дроби равен пределу числителя, деленному на предел знаменателя, если последний не равен нулю.

Кроме этих теорем широкое применение имеют два замечательных предела:

1. Предел отношения синуса бесконечно малой дуги к самой дуге равен единице.

, или . (4.1.1)

2. Предел выражения:

или . (4.1.2)

Рассмотрим применение указанных теорем в решении конкретных примеров.

Пример 13.

Вычислить предел

Решение:

а) Подставив предельное значение аргумента в заданное выражение, получим неопределенность вида , для раскрытия которой числитель и знаменатель дроби разложим на множители, найдя предварительно корни трехчленов.

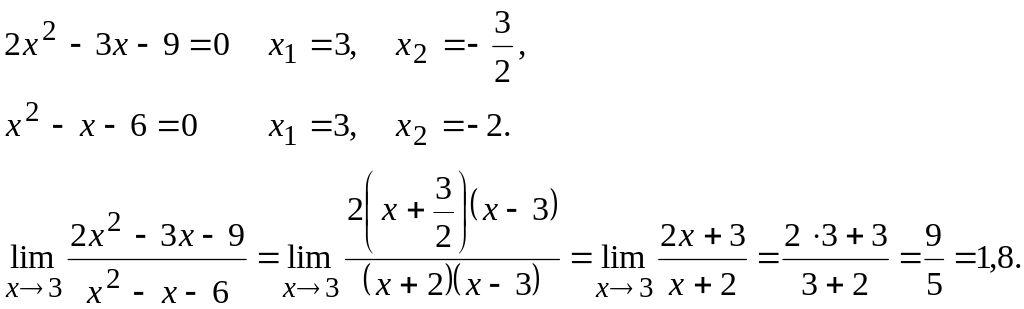
б) Подстановка предельного значения х показывает, что имеем неопределенность вида , для раскрытия которой числитель и знаменатель дроби делим почленно на .При этом получим пределы вида и т. д., которые равны нулю.

.

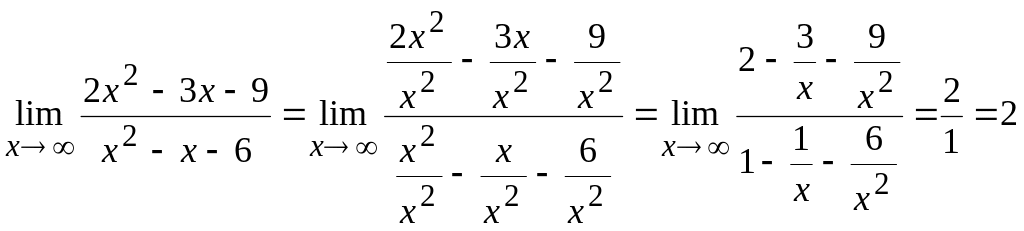Пример 14.

Вычислить предел .

Решение:

Нетрудно убедиться, что имеем неопределенность , которая в отличие от предыдущего примера, содержит иррациональность в числителе.

Чтобы освободиться от этой иррациональности, умножим числитель и знаменатель дроби на выражение, сопряженное числителю. Применив затем формулу разности квадратов двух чисел и упростив числитель, можем сократить дробь.

Оставшаяся дробь не содержит нуль в знаменателе и дает возможность арифметического подсчета.

=

= .

Пример 15.

Вычислить предел .

Решение:

Преобразуем данное выражение:

В каждом сомножителе выполним несложные преобразования, позволяющие применить 1-ый замечательный предел:

.

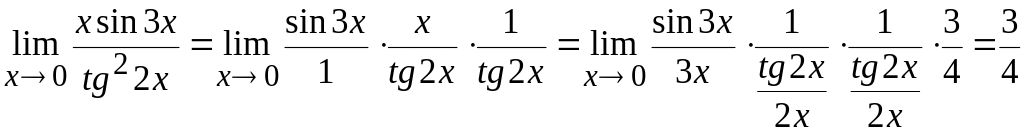Пример 16.

Вычислить предел

Решение:

Преобразуем исходное выражение так, чтобы использовать 2-ой замечательный предел.

Выделим внутри скобки единицу, сделаем замену переменной и преобразуем показатель степени.

= = = .

4.1 Вопросы для самопроверки

1. Что называется пределом функции в точке х=а?

2. Назовите основные теоремы о пределах.

3. Сформулируйте два замечательных предела.