Вопросы по проверке знаний по курсу

"ГИДРОДИНАМИКА ЭНЕРГЕТИЧЕСКИХ УСТАНОВОК"

МОДУЛЬ 1

1. Уравнение изменения количества движения в обогреваемой трубе и его интегрирование для установившегося режима.

Для вывода уравнения, возьмём элемент трубы длиной , с площадью поперечного сечения , наклонённую к горизонту под углом .

Действие от оставшейся трубы на входное и выходное сечение заменим статическими давлениями на входе , на выходе .

Применительно к выделенному элементу применим второй закон Ньютона  произведение массы на ускорение равно сумме действующих на массу сил.

(2)

Масса жидкости в объём элемента равна .Вес этой массы .

При движении жидкости на внутренней поверхности элемента возникают касательные напряжения , создающие силу трения .

Кроме этого со стороны входа действует сила давления , а со стороны выхода .

Таким образом, сумма действующих на массу жидкости сил в направлении оси (в уравнении 2) будет равна

.

Выразим полную производную , представляющую ускорение массы жидкости. Так как скорость является функцией двух переменных , то

.

Подставив значения , и в уравнение 2, получим

.

Для развитого турбулентного движения .

Тогда и уравнение изменения количества движения примет вид

. (3)

В уравнении для касательных напряжений  коэффициент сопротивления трению. Для области турбулентного движения (автомобильная область) он зависит только от шероховатости и определяется по формуле

,

где  величина шероховатости, м;

 радиус трубы, м.

2. Уравнение сохранения энергии для рабочего тела в обогреваемой трубе и его интегрирование для установившегося режима.

Рассмотрим баланс энергии на элементе трубы длиной (рисунок 4).

Рис. 4 – баланс энергии на элементе трубы

На вход в элементе поступает энергия (в единицу времени), а выходит .

Кроме того с внутренней поверхности в рабочее тело поступает теплота в количестве , где  плотность теплового потока на внутренней поверхности трубы. В нестационарном процессе часть энергии аккумулируется внутри массы жидкости .

Тогда уравнение сохранения энергии для рабочего тела примет вид:

.

Разделим все члены уравнения на объём элемента

. (4)

преобразуем частные производные:

; .

и подставим их в уравнение (4):

.

0

Из уравнения неразрывности следует, что

.

Тогда уравнение сохранения энергии для рабочего тела примет вид:

(5)

где  внутренний периметр трубы;

 площадь сечения для прохода рабочего тела.

3.Система уравнений, описывающая движение рабочего тела в обогреваемой трубе.

В установившемся режиме движение переменные параметры среды в любом поперечном сечении трубы не меняются во времени, т.е. все параметры являются только функцией продольной координаты . Все локальные производные , где под «у» понимаются переменные параметры.

В соответствии с этим исходная система уравнений, описывающая движение жидкости в обогреваемой трубе для установившегося режима примет вид:

1)  уравнение неразрывности;

2)  уравнение изменения количества движения;

3)  уравнение сохранения энергии для рабочего тела;

4)  уравнение сохранения энергии для металла трубы;

5, 6) замыкающие зависимости и уравнения состояния остаются без изменения.

Интегрирование системы уравнений начнём с уравнения неразрывности. . Равенство нолю производной выполняется, когда переменная постоянна. Как уже отмечалось ранее, произведение равно массовому расходу , который сохраняет своё значение в любом поперечном сечении трубы.

Если труба имеет постоянный диаметр, то массовая скорость также постоянна в любом сечении, т.е. где индексы «н» и «к» относятся к сечению на входе и выходе из трубы.

Из постоянства массового расхода следует, массовая скорость зависит от поперечного сечения трубы и может изменяться, если : , где  площадь поперечного сечения трубы с координатой .

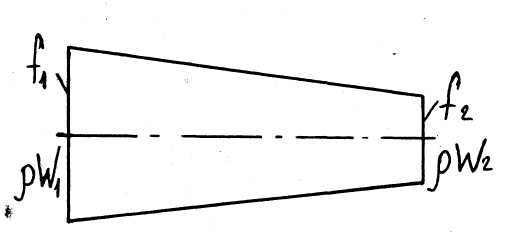
Рисунок

Зная массовый расход «D» и площадь сечения легко найти массовые скорости в этих сечениях из уравнения неразрывности:

, откуда

.

В необогреваемой трубе энтальпия не меняется вдоль трубы, поэтому в соответствии с уравнением состояния плотность среды также остаётся постоянной.

Линейная скорость в силу постоянства массовой скорости в этом случае не меняется вдоль оси.

Для обогреваемой трубы в каждом сечении трубы плотность будет разная, т.к. энтальпия потока увеличивается в направлении движения. Как видно из рисунка 5, 6. С увеличением энтальпии плотность уменьшается, что вызывает рост линейных скоростей , при этом , согласно уравнению неразрывности.

Проинтегрируем уравнение сохранения энергии для рабочего тела.

 это уравнение с разделяющимися переменными.

. (10)

В соответствии с уравнением неразрывности, массовая скорость в установившемся режиме для трубы поперечного сечения является постоянной величиной. Постоянны также периметр и внутренний диаметр трубы.