Характеристики динамических звеньев

Вся информация о возможных вариантах поведения динамического звена содержится в его уравнении и численных значениях параметров звена. Эта же информация содержится и в характеристических функциях звена. Основными характеристиками являются уже знакомые нам передаточная функция и переходная функция .

Первая из них позволяет по заданному входу найти выход звена, а вторая – является ответной реакцией звена на случайное воздействие в форме функции Хевисейда

Поскольку образ функции Хевисейда имеет вид

,

то образ переходной функции

,

а если переходная функция равна

,

где - обратное преобразование Лапласа.

Не менее важной характеристикой является частотная характеристика звена, которая отображает реакцию звена на гармоническое входное воздействие заданной частоты . Амплитуда выходных колебаний равна , а сдвиг по фазе .

Например, для инерционного звена (2.9) пусть . Тогда

,

образ выхода равен

.

Последнее выражение можно разделить на элементарные сложения

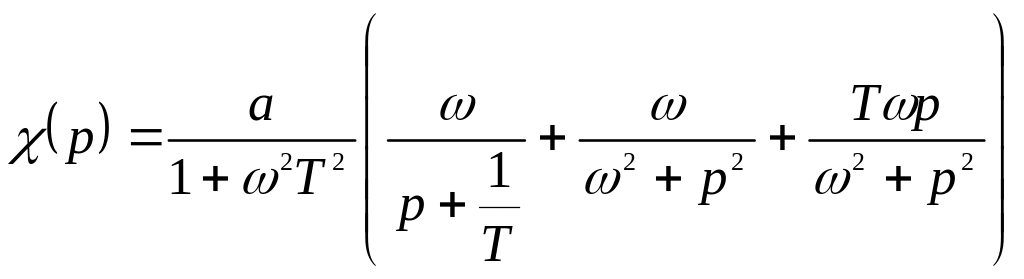
и найти прообраз выхода

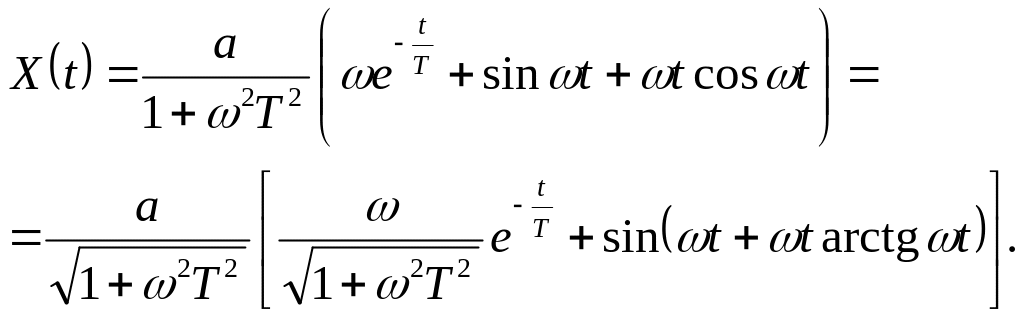
Этот процесс состоит из быстрозатухающего экспоненциального процесса и вынужденных гармонических колебаний со сдвигом по t относительно входа.

Частотная характеристика звена

содержит все сведения об амплитуде и сдвиге по фазе вынужденных колебаний. Так радиус равен амплитуде выхода, а аргумент – сдвигу по фазе с обратным знаком.

Для анализа поведения системы в условиях периодических воздействий, её реакции как раз и необходимо знание частотной характеристики звена.

В качестве другой характеристики, являющейся реакцией системы на специальное возмущающее воздействие, используется импульсная функция. Эта функция описывает поведение системы после того, как на находящуюся в свободном состоянии систему воздействует импульсное воздействие в форме дельта-функции (функции Дирака)

.

Учитывая это, образ -функции , для образа импульсной функции получим

,

а сама импульсная функция равна

,

где - обратное преобразование Лапласа.

В определённой мере импульсная функция характеризует устойчивость системы, её способность возвращения в исходное состояние.

Например, для инерционного звена (2.9) и, используя таблицы обратных преобразований Лапласа, получим

.

Таким образом, инерционное звено, будучи выведенным из состояния покоя импульсным воздействием, с течением времени возвращается в начальное состояние.

2.2. Математические модели линейных динамических систем

Математическая модель линейной динамической системы может быть представлена на основе математических моделей элементов и звеньев, образующих систему. Линейная система в общем случае состоит из звеньев, соединенных последовательно, параллельно и обратными связями. Передаточные функции (ПФ) таких структур выражаются через ПФ типовых звеньев.

При последовательном соединении элементов (рис.2.4,а) выход первого звена является входом второго.

Рис.2.4. Схемы последовательного - а и параллельного - б соединения элементов

Таким образом, можем записать

,

а для всей структуры в целом получим ПФ

. (2.30)

При параллельном соединении элементов (рис. 2.4,б) можем записать:

а значит,

. (2.31)

Рассмотрим также ПФ звена, охваченного обратной связью (рис.2.5).

Рис. 2.5. Схема звена, охваченного обратной связью

Из рисунка изображающего связь сигналов можно записать уравнения:

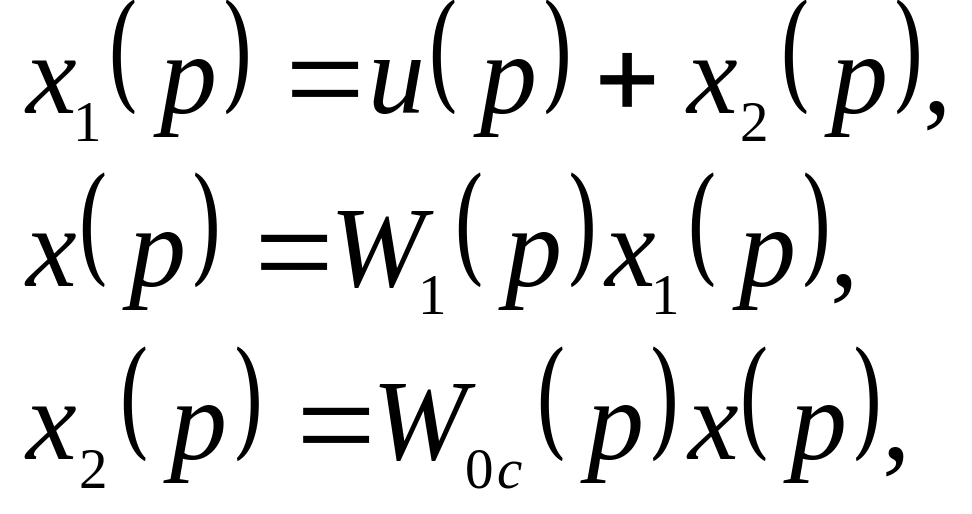
из которых можно получать:

или, в конце концов:

.

Можно отметить, что если сигнал обратной связи складывается с входом, то говорят о положительной обратной связи, если же сигнал обратной связи вычитается из входа, то говорят об отрицательной обратной связи и в общем случае можно записать для передаточной функции системы, охваченной обратной связью

(2.32)

где знак (-) соответствует положительной обратной связи, а знак (+) – отрицательной. Отрицательная обратная связь способствует устойчивости системы. Если обратная связь охватывает целиком систему, то говорят о цепи главной обратной связи.

Если обратные связи охватывают систему частично, то возможно упрощение схем. Например, для перекрестных обратных связей (рис. 2.6) можно изобразить эквивалентную схему, передаточная функция которой эквивалентна исходной (рис. 2.7), но её расчёт гораздо проще.

Рис. 2.6 Схема с перекрестными обратными связями

Рис. 2.7. Один из вариантов преобразованной схемы с перекрестными обратными связями

Например, для схемы рис. 2.7 можно, используя формулы обратных связей и последовательного соединения, записать

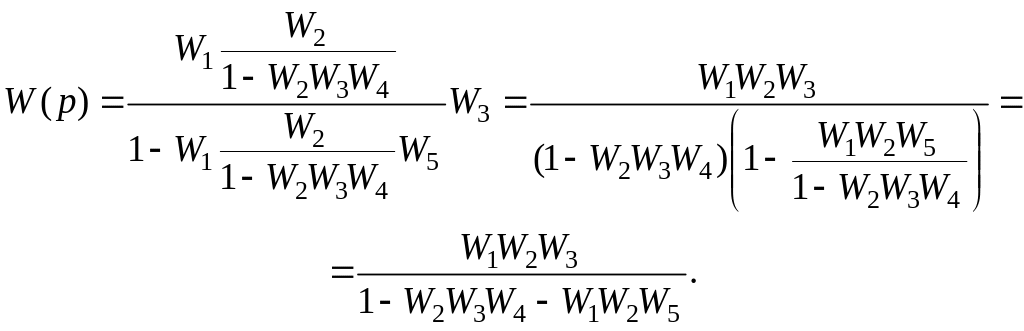
Для схемы общего вида можно пользоваться формулой Мейсона, полученной для так называемых сигнальных графов, в которых дуга имеет вес передаточной функции звена. Сама формула имеет вид

, (2.33)

где G - передаточная функция к-го разомкнутого пути, соединяющего вход и выход;

, (2.34)

где - произведения передаточных функций дуг (звеньев) m-го сочетания из n непересекающихся контуров (циклов);

- имеет тот же вид, что и D в (2.34), но в части графа, не соприкасающейся с к-ым разомкнутым путем.

На рис. 2.8 продемонстрировано применение правила Мейсона для схемы рис.2.6, откуда сразу можно записать

. (2.35)

Рис. 2.8 Применение правила Мейсона

Д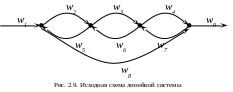 ля более сложного варианта схемы можно рассмотреть рис. 2.9, где представлена схема системы, а на рис. 2.10 представлены поэтапно элементы формирования передаточной функции по формуле Мейсона.

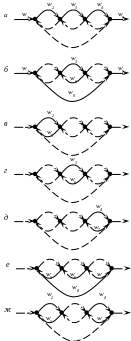
Рис. 2.10. Применение правила Мейсона

Используя результаты, представленные на рис. 2.10, можно легко записать результат:

.

Если входные воздействия приложены в нескольких точках системы, то, учитывая ее линейность, можно сразу сказать, что реакция на выходе определится суммой реакций на каждое входное воздействие.

,

где , и - есть произведение передаточных функций звеньев, включенных между i-ым входом и выходом, - передаточная функция разомкнутой схемы (см. формулу (2.35) и рис. 2.6).