2. Линейные динамические системы

2.1. Математические модели звеньев линейных динамических систем

Линейными называются системы управления (СУ), которые в статике и в динамике описываются линейными уравнениями. Линейность уравнений подразумевает их однородность и аддитивность, что обусловливает применяемость принципа суперпозиции, в соответствии с которым реакция системы на совокупность возмущений определяется суммой реакций на каждое из возмущений, приложенных к системе в данный момент.

В реальности истинно линейных систем мало, однако в большинстве случаев линеаризация моделей систем управлений позволяет получить достаточно эффективные линейные модели, которые зачастую не приводят к недопустимым погрешностям при анализе и существенно упрощают исследование систем.

Динамические режимы линейных СУ исследуются с помощью их математических моделей, причем любую динамическую систему можно представить в виде комбинаций типовых структурных звеньев: апериодических, колебательных, интегрирующих, дифференцирующих и усилительных.

Действительно, если система описывается линейным дифференциальным уравнением вида

, (2.1)

где , вход и выход системы, , - их k-е производные по времени и обычно , то с помощью преобразования Лапласа (1.4) для любой линейной динамической системы получим

. (2.2)

где , изображения входа и выхода соответственно.

Алгебраическую дробь (2.2) можно разложить на элементарные слагаемые вида:

(2.3)

(2.4)

где не имеет действительных корней.

Тогда нам достаточно рассмотреть основные звенья, имеющие передаточные функции , определяющие отношение выходного сигнала y к входному :

, (2.5)

, (2.6)

, (2.7)

, (2.8)

и на их основании можно получить любые, сколь угодно сложные модели систем.

Апериодическое звено

Апериодическим называется звено, в котором связь между выходной (х) и входной (u) величинами описывается уравнением

, (2.9)

где - коэффициент усиления (передачи) звена; - постоянная времени звена. Величины и являются характеристиками реальных свойств звена. Иногда звенья, описываемые уравнением (2.9), называют инерционными.

Применяя к уравнению (2.9) преобразование Лапласа при нулевых начальных условиях , получим:

,

то есть передаточная функция звена равна

. (2.10)

Если решить уравнение (2.9) относительно , то получим

. (2.11)

При единичном входном воздействии: , при и при получаем переходную функцию звена, описывающую процесс перехода системы из начального состояния в стационарное.

. (2.12)

Если уравнение апериодического звена имеет вид

, (2.13)

то передаточная функция представляется как

, (2.14)

а переходный процесс описывается уравнением

.

На рис. 2.1 изображены переходные процессы в звеньях типа (2.9) и (2.13).

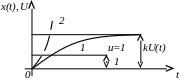
Рис. 2.1. Переходный процесс в апериодическом звене

1 – для уравнения (2.9); 2 – для уравнения (2.13)

Очевидно, что звено, описываемое уравнением (2.9), является устойчивым, т.к. величина ограничена сверху, а описываемое уравнением (2.13) – неустойчивым, что следует из того, что неограниченно возрастает с ростом .

Пример 2.1. Рассмотрим состояние основных фондов на предприятии. Прежде всего учтём, что они убывают со временем. Так, если в момент они были равны , то из-за старения в момент они составят

,

где – некоторая убывающая функция, такая что . Точно так же фонды , введенные в интервале времени , где - темпы ввода фондов, к моменту составят величину . Тогда для фондов можно записать

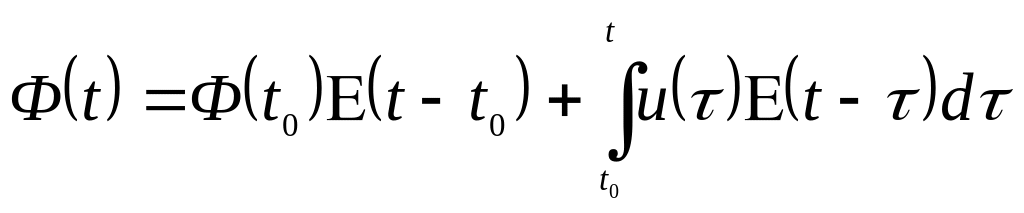. (2.15)

Обычно полагают

, (2.16)

где .

Продифференцировав (2.15) с учетом (2.16), получим

.

Таким образом, мы получили уравнение звена типа (2.9).