7. Идеи вариационного исчисления.
В оптике траєкторию лучей можно найти из принципа наименьшего времени, а в механике, из принципа наименьшего чего? Такая величина называется действием S . Впервые понятие действие рассмотрел Лейбниц, считал, что
или
1744-47 гг. появились работы Мопертюн, который провозгласил принцип наименьшего действия как фундаментальный закон природы, доказав существование Бога.
Понятия, используемые в вариационном исчислении:
1. Функционал – переменная, определенная на области функции
Время, которое требуется на преодоление расстояния между A и В, зависит вида ф-ции y(x). Если задачей диф. исчисления является нахождения экстремума ф-ции, то задачей вариационного исчисления является нахождение экстремума ф-ционала.
2. Экстремаль – ф-ция y(x), при которой ф-ционал принимает макс. или мин. значения.
,
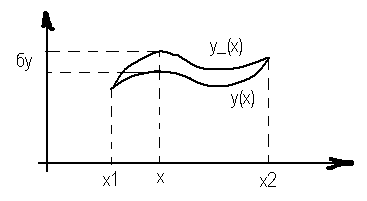
где
L – ф-ция Лагранжа.
38.Закон сохр энергии как следствие однородности времени.
Однородность времени (ОВ).
Под
ОВ понимают независимость механического
состояния системы от времени (отсутствие
полей или сил, меняющихся со временем
). В глобальном
смысле:
равноправие законов физики в различные
моменты времени. Следствие:
ф-я Лагранжа
явно не должна зависеть от времени, а
именно DL/Dt
= 0, а полная производная –
необязательно:=>
-Энергия
системы. В общем случае кинет. эн-я может
быть предст. в виде:
Вместо
i
можно написать k:
36. Закон сохр импульса как следствие однородности пространства.
Однородность пространства (ОП)
Под ОП понимают независ. мех. сист. от положения пространства. Все точки пространства равноправны:
Ур-е
Л.-Э.
;
-
обобщ. импульс;
-
обобщ. сила. В декартовых корд.:
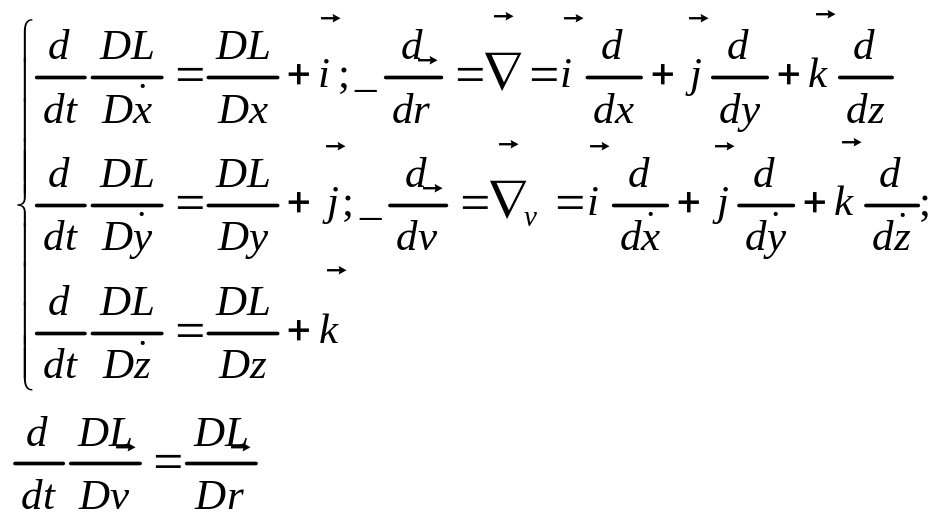Ур-я
Л.-Э. могут быть записаны в виде:
сместим
все частицы системы на один и тот же
вектор
бесконечно
малый. Если простр. однор., то соотв.
этому смещению изменение ф-ии Л. должно
= 0.
,
В
виду произвольности ε данное равенство
возможно в том случае , если :
-полный
импульс силы
.
37. Закон сохр момента импульса - как следствие изотропии пространства.
Изотропия пространства
Повернем
сист. частиц на бесконечно малый угол
,
если
пространство изотропно то
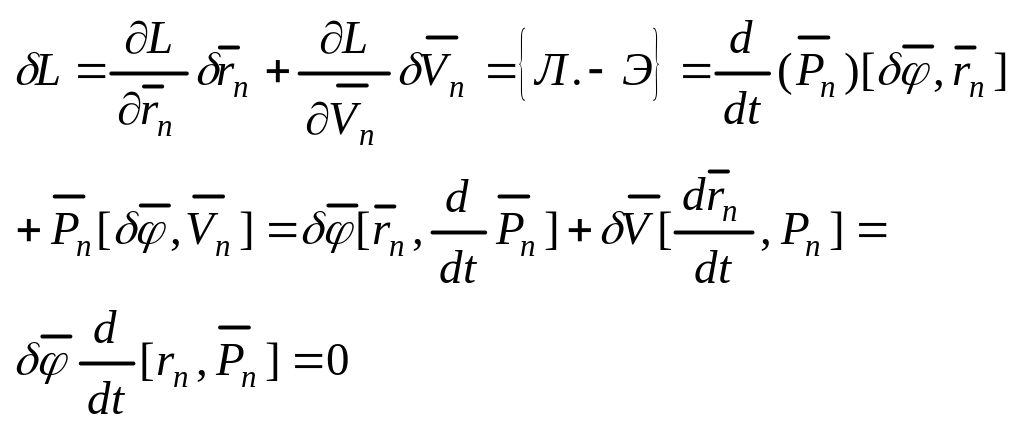
в
виду независимости
данное
равенство возможно если:
-полный
момент импульса.
35.Ф-я Лагранжа и ее свойства.
Рассмотрим
случай со свободной частицей. В виду
равноправия различных положений в
пространстве, ф-я Лагранжа от координат
зависеть не должна. В виду равноправия
направлений ф-я Л. зависит от квадрата
скорости: L=L(V2).
Для нахожд. явной зависимости воспользуемся
принципом относительности Галилея, но:
замечания относительно св-в ф-ии Лагранжа:
1. Ф-ю
Лагранжа можно умножать на произвольную
постоянную L=>CL.
2.
К ф. Л. можно прибавить произв. по времени
от некоторой ф-и координаты времени
3.
Ф-я Л. системы невзаимод. частиц = сумме
ф-ии Лагранжа
переход к другой инерц. сист. стсчета не должен изменять ур-е движения и вид ф-ии Лагранжа.
21.Скорость в цилиндрической системе координат.
Цилиндрическая система
- расстояние от оси OZ до части
-проэкция на XoY
- угол между осью 0X и проэкцией на XoY.
;
z(-;+) – такая же как и в декартной системе
;
; ;
( ц)