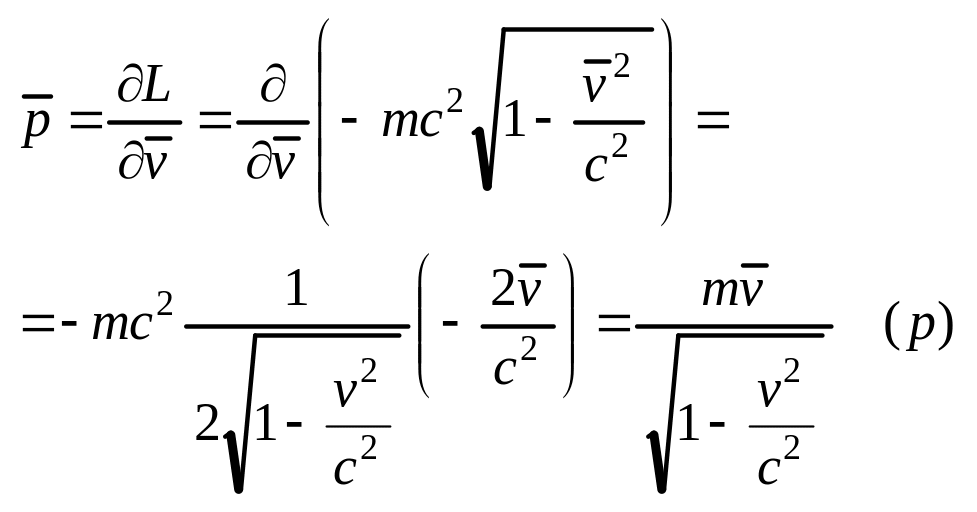30. Закон изменения и сохранения импульса в Ньютоновой механике

ЗСИ

Nчастиц

Сложим подобные выражения для всех частиц системы

;

Изменение импульса происходит под воздействием внешних сил действ. на систему. Если внешними силами можно пренебречь, то импульс системы сохраняется

20. Вириальная теорема

Устанавливает связь между средней кинетической энергией системы, действующей в этой системе.

(усредняем по времени) (1)

площадь прямоугольника = площади кривол. траектории.

Если рассматривать большие значения τ

Оказывается, среднее значение по бесконечно большому промежутку времени от полной производной по времени ограниченной функции =0

, где F –огранич. (не сводится к бесконечности )

В нашем случае , если система частиц не разлетается на бесконечность, то 1-е слагаемое в уравнение (1)=0

Просуммируем : Вириал сил

Предположим, что силы, действ. в системе , потенц.

То есть :

и

В этом случае вириальная теорема принимает вид:

Предположим

(гравит. ; , Кулон , Осциллятор )

Тогда:

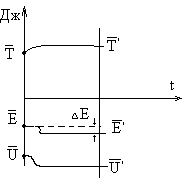
Звезда на поздних этапах эволюции исчерпала топливо (его термоядерные запасы ). Как с течением времени должна меняться температура звезды?

Вещество в звезде связано гравитационными силами

где Т –кинетическая, а U –потенциальная энергии.

звезда сжимается => температура повышается сжатие останавливается, из-за квантовой мех- и

44. Условия равновесия. Виды равновесия. Период малых одномерных колебаний.

Точки устойчивого и не устойчивого равновесия.

В положении равновесия F=0, F=-U^’(q₀)=0

При устойчивом равновесии потенциальная энергия имеет минимум и так как Условия устойчивого равновесия:

Если первая отличная от нуля производная окажется производной чётного порядка и будет больше нуля , то соответствующая точка будет точкой устойчивого равновесия .

6. Период малых колебаний вблизи точек устойчивого равновесия .

Пусть т.q₀- точка устойчивого равновесия , отсюда

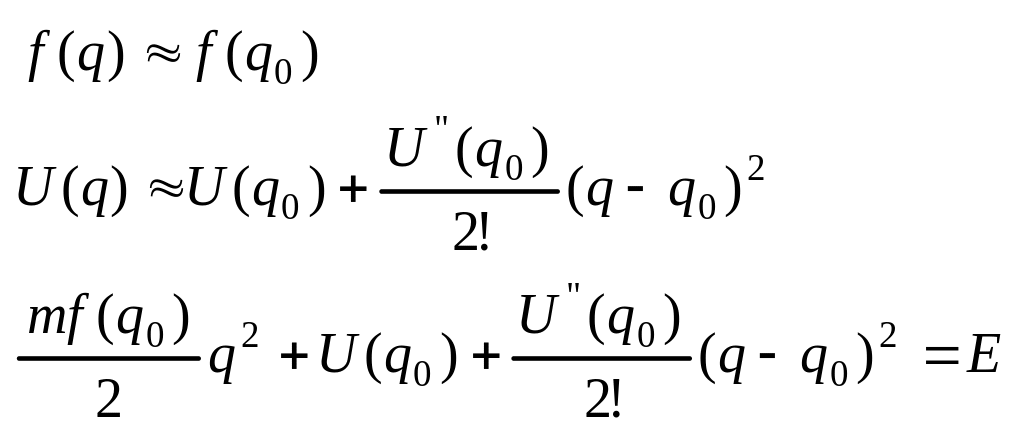
Пусть q₀- точка устойчивого равновесия. Это означает U’(q₀)=0 U”(q₀)>0. Разложим ф-цию в ряд

Подставим вместо

-

ур. гармонических колебаний .

Физический маятник.

, берем производную

17. Система центра масс. Задача двух тел.

В системе центра масс задача двух тел сводится к одномерному случаю с потенц. энергией

Особенность заключается в том, что в точках поворота тело не останавливается, т.к. .Частица либо удаляется на наибольшее, либо приближается на наименьшее расстояние от центра.

падение на центр поля:

, отсюда

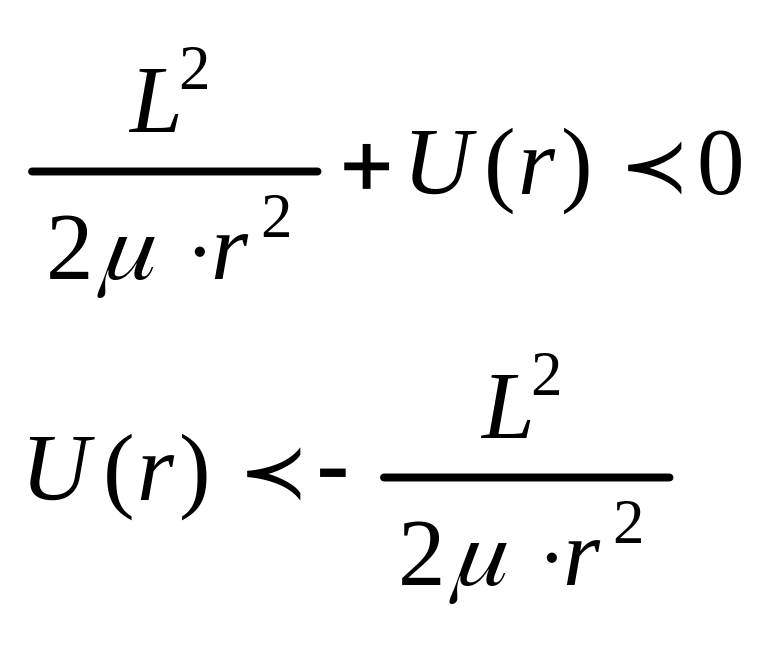
Пусть , тогда

Падение возможно, если

(при ), и невозможно, если . Для гравит. и кулоновск. поля n=1 (падение на центр поля невозможно).

34. Ф-ция Лагранжа свободной релятивистской частицы. Импульс и энергия.

Ф-ция Лагранжа релятивистской частицы в 3-х мерном пространстве.

- прямая, траектория движения свободной частицы.

В СТО кроме координат вступает время (3 коорд. + время)

(по аналогии)

Т.о. S –действия для релятивистской частицы.

;

обобщённый импульс

, где