19. Кинетическая энергия твердого тела. Тензор инерции
Твердое тело –тела расстояние между двумя точками которого неизменно.
-тензор
-скаляр
П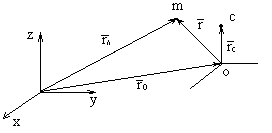
редположим,
что центр подвижной системы отсчета
связан с какой то точкой твердого тела.
(1)
Точка
m
также принадлежит телу. Тогда при
движении твердого тела
(2)
Тогда
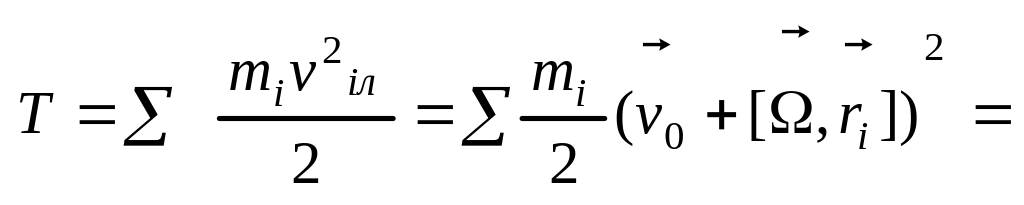
Если
точка О совпадает с центром масс, тогда
где
(3)-тензор
инерции
В случае непрерывного распределения вещества
28. Секторная скорость в СфСк.
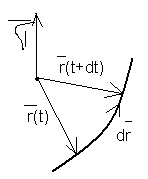
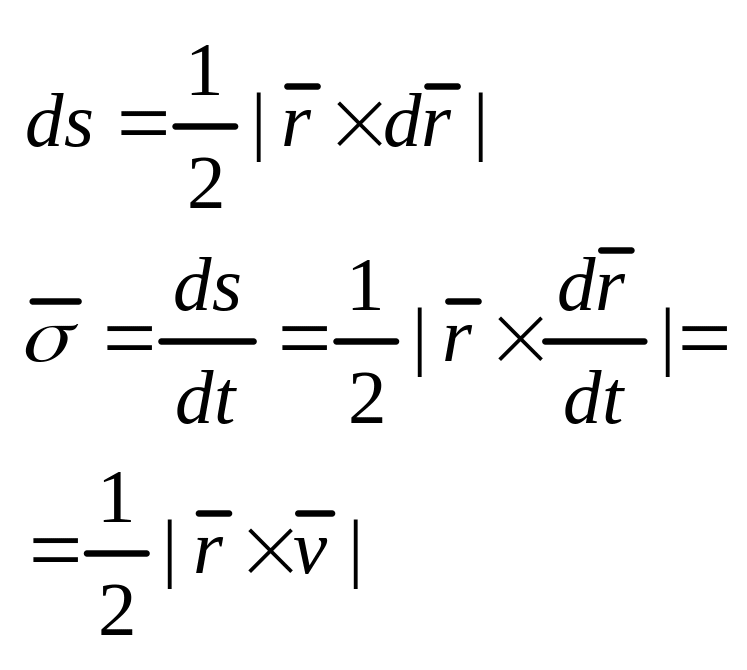
Сферическая С.К.
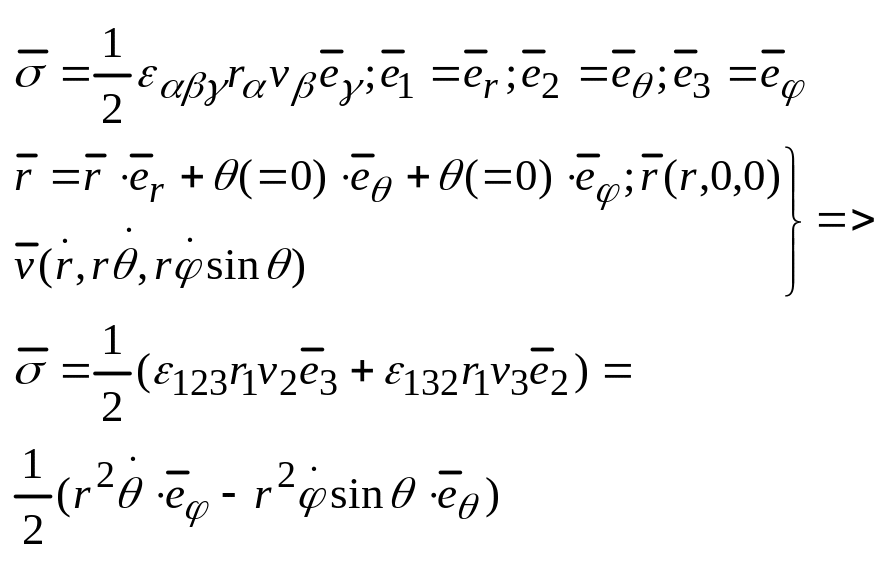
26. Секторная скорость дск.
2. Декартова С.К.
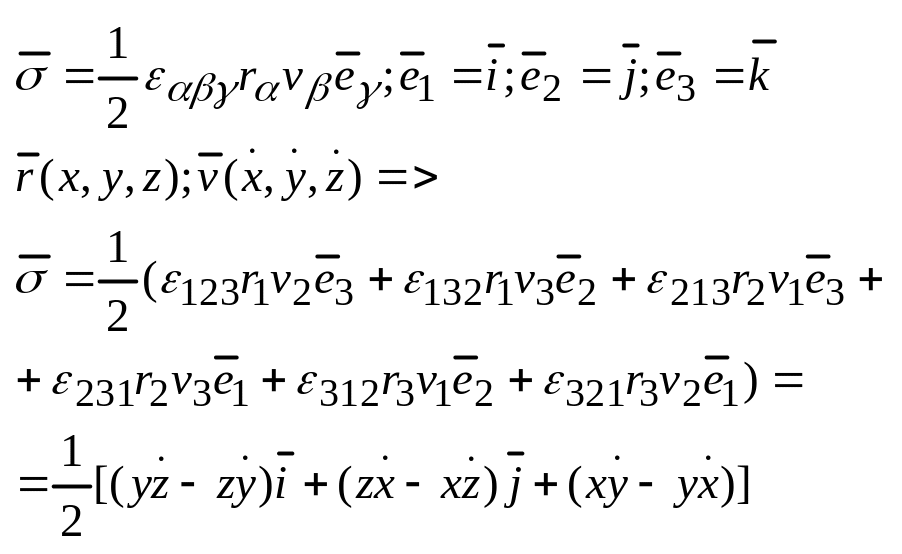
27. Секторная скорость в цск.
Цилиндрическая С.К.
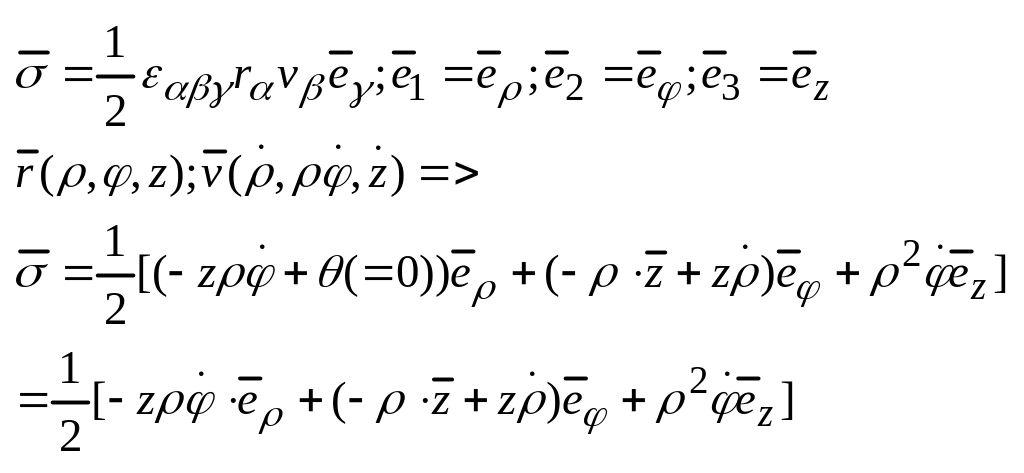
10. Ф-я Гамельтона. Каноническаие
Уравнения Гамельтона.
H(q,p,t) найдем вид ф-ции Н
(1)
-
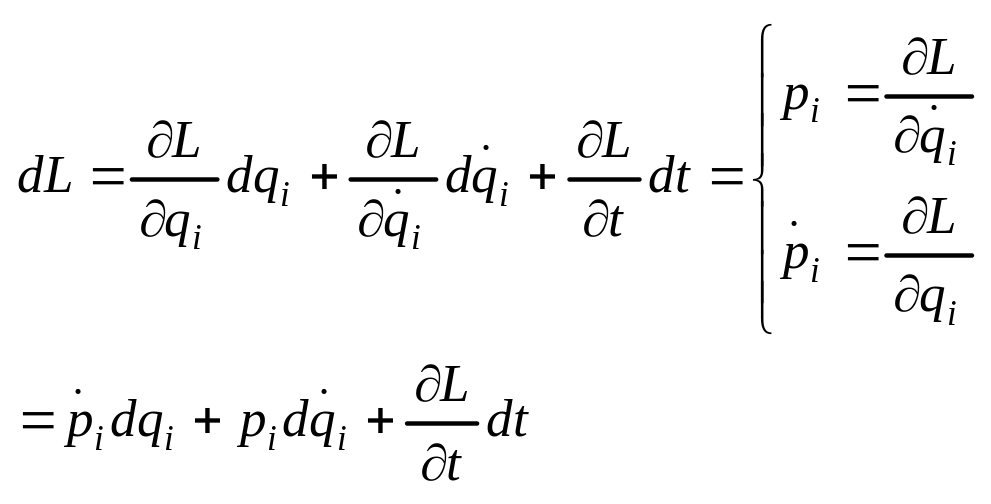
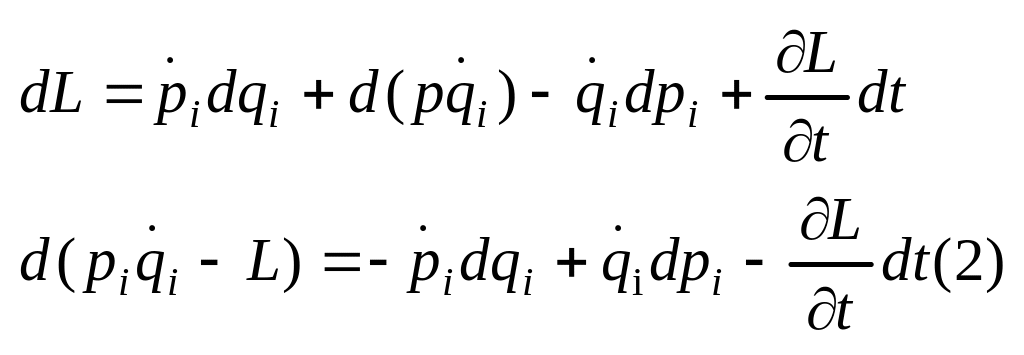
Ф-я Гамильтона
-
Канонические Ур-я Гамильтона
Поскольку Н – функция коорд. импульса и времени (Н) –(5) диф. уравн. 1-го порядка.
11. Скобки Пуассона и интегралы движения.
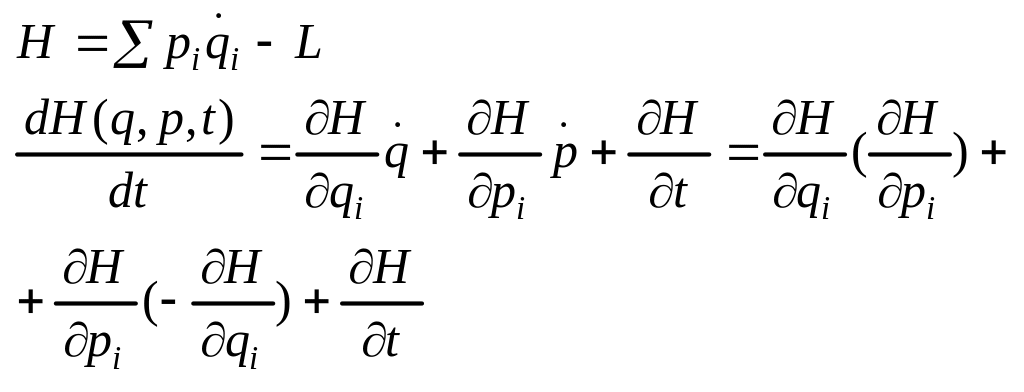
Если
в выражение для ф-ции Г. время в явном
виде не входит
В этом случае ф-ция Г. имеет смысл полной энергии системы : H=T + U. Рассмотрим полную производную по времени от произвольной ф-ции Гамильтоновой механики
-
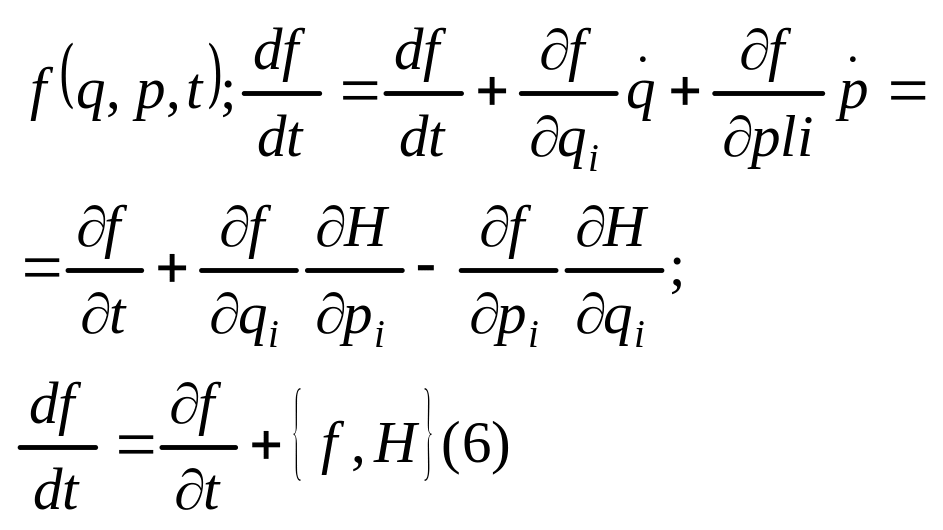
скобка Пуассона
12. Свойства скобки Пуассона. Фундаментальные скобки Пуассона
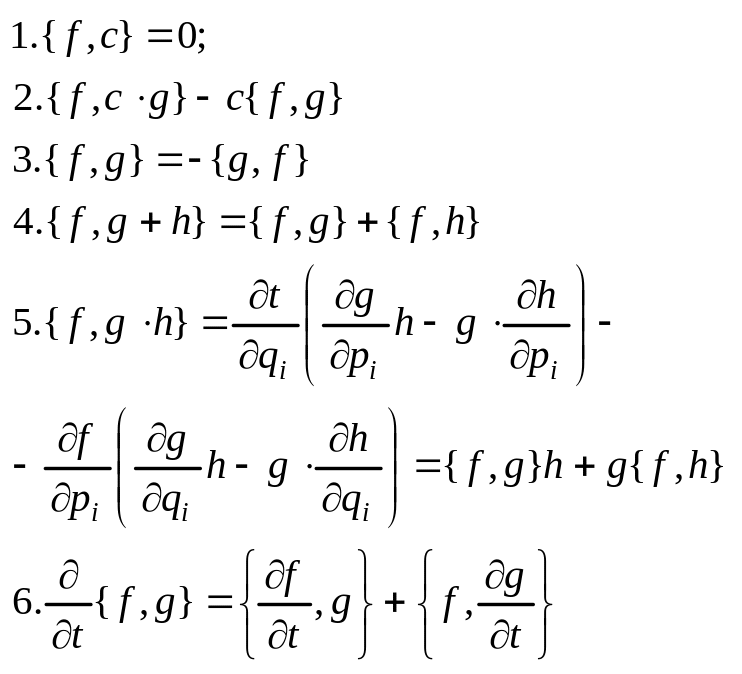
Тождество Якоби:
Фундаментальные скобки Пуассона:
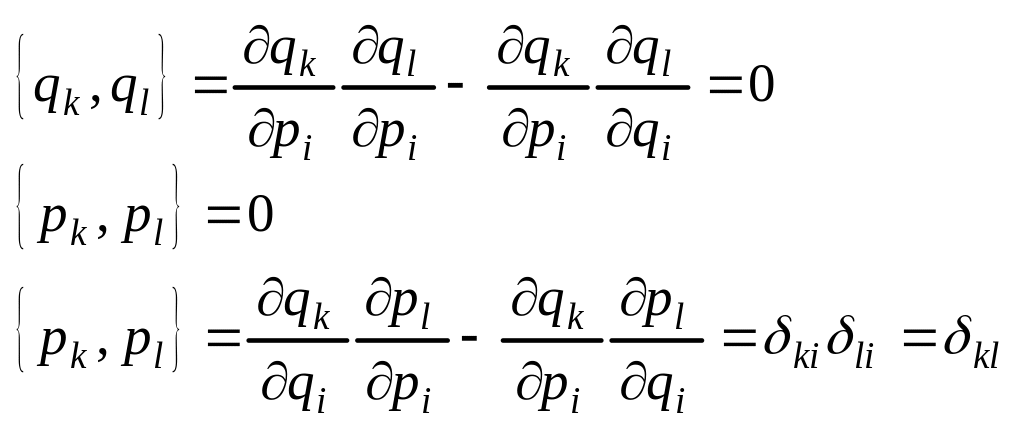
(4)
(5)
40. Теорема Пуассона
Если f,g – интегралы движения, то их скобка Пуассона также интеграл движения
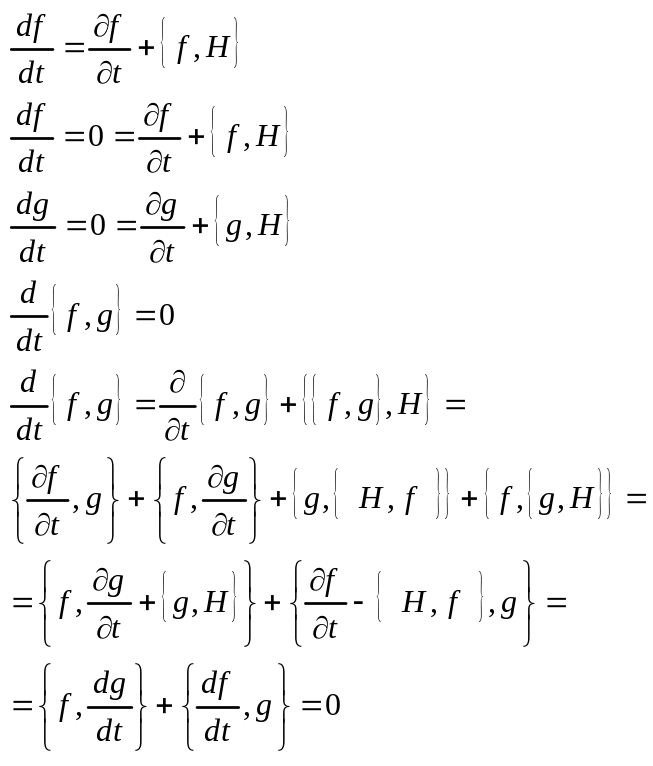Пример:
предположим, что в некотором поле
сохраняется
и
.
Найти еще один интеграл движения (сохр.
величину)
Согласно
теор. Пуассона:Пуассона: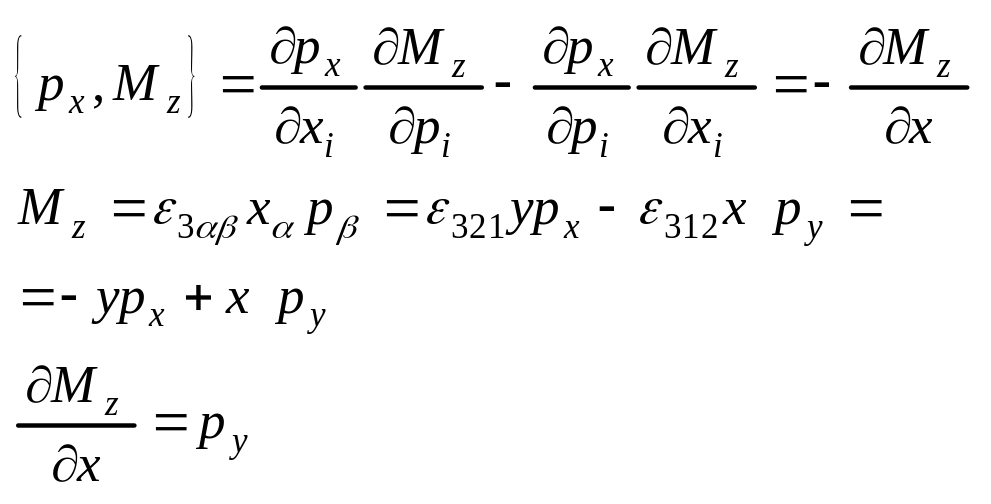
2-ой способ:
33. Потенциальное поле. Условие потенциальности.
Условие потенциальности сил
;
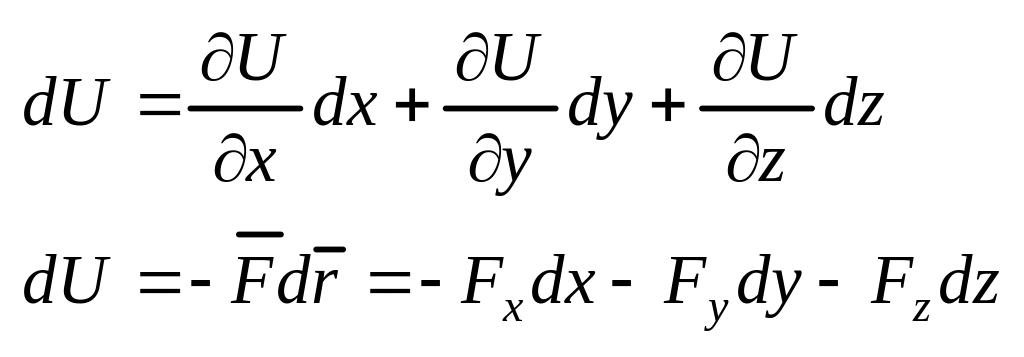
По свойству частных производных
условие
потенциальности поля
2. Если работа не зависит от пути перемещения тела, то…
По теореме Стокса:
-дивергенция
ротор в декартовой системе координат
Получим систему (3)
1. Описание движения в декартовой системе координат. Элементы длины и объёма, вектор градиента.
Декартова система
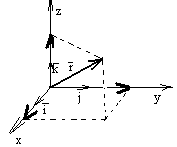
x(-;)
y(-;)
z(-;)
;
;
2. Описание движения в цилиндрической системе координат.
Цилиндрическая система
-
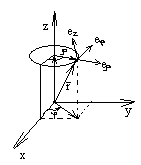
расстояние от оси OZ
до части
-проекция
на
XoY
- угол между осью 0X и проекцией на XoY.
;
z(-;+) – такая же как и в декартовой системе
;
;
;
(
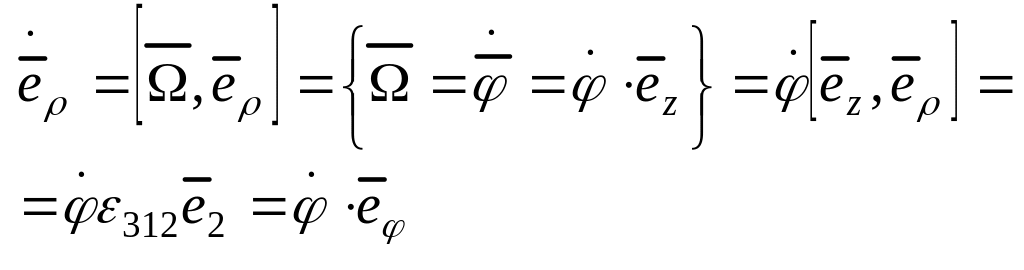ц)
;
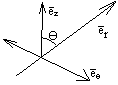
3. Описание движения сферической системе координат
-
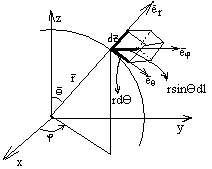
расстояние от начала координат до точки,
это радиус-вектор
-
угол между осью OZ
и радиусом-вектором
-угол между осью OX и проэкцией радиус-вектора.
;
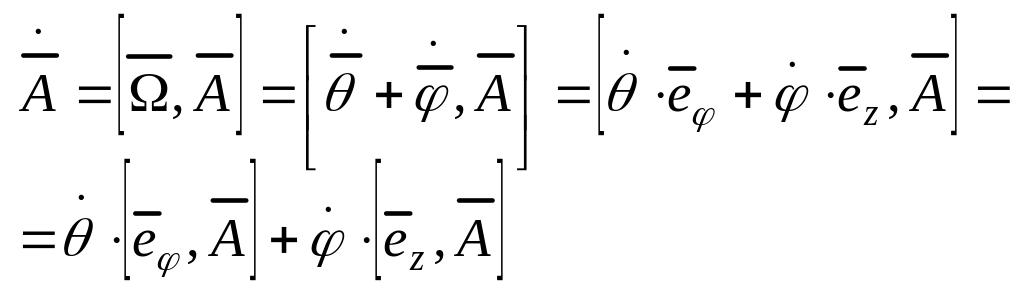
-это(
)
-это
(
С)
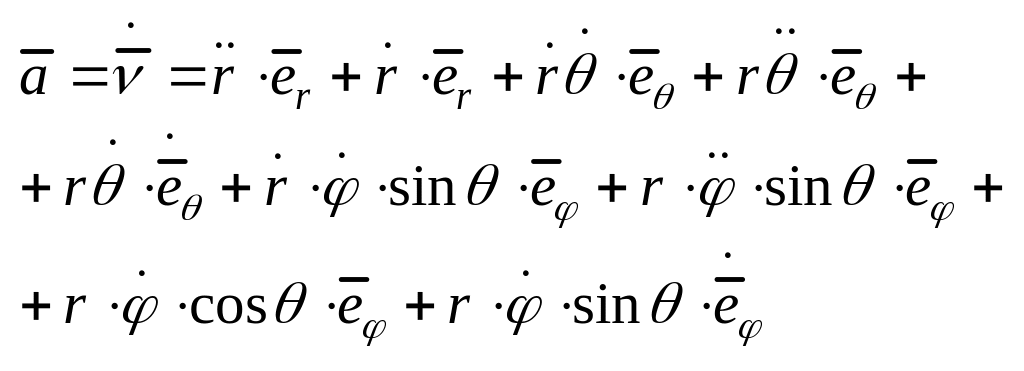
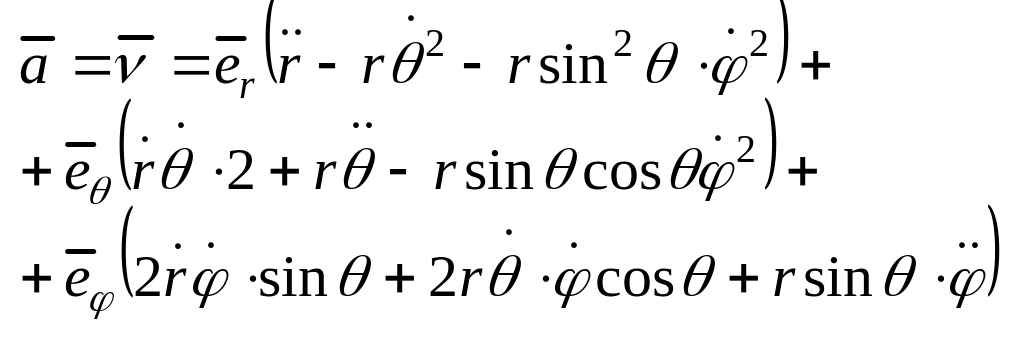
-это(а С)
;
;
;
;
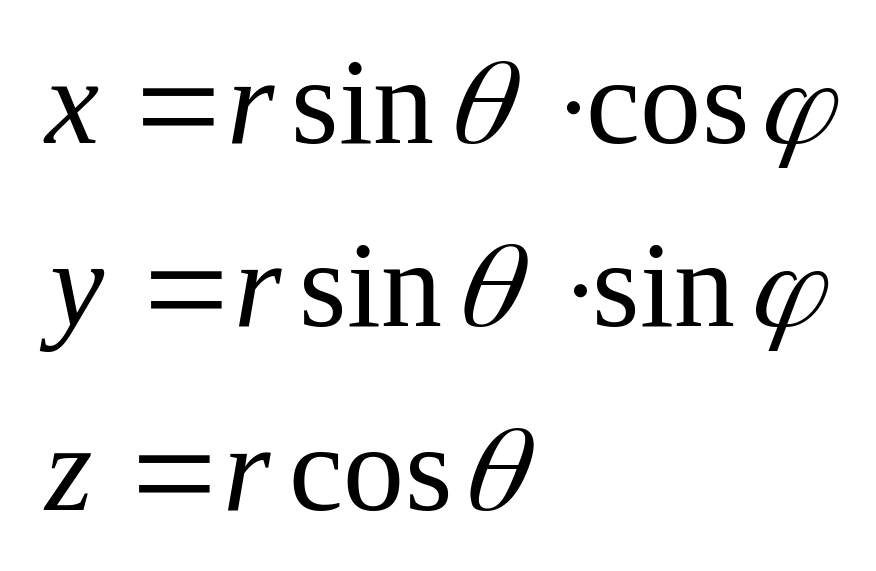
4.Законы Ньютона – основа клас механики. Внутр и внешние силы.
1. Существуют такие системы отчета относительно которых частица свободно движется равномерно и переменно переменно прилюбых начальных условиях. Это инерциальные системы отчета. Систематически они движутся относительно инерцый с спостояной скоростью также инерцыей.
2.Изменение импульса тела в еденицу времени равна сумме сил, действующих на это тело.
(
,
если
)
Используются принципы независимости
друг от друга и принцип суперпозиций.
Вид
2-го закона Ньютона для неинерциальных
систем отсчета:
3. Две частицы взаимодействуют с силами противоположными по направлению, равными по величине и действующие вдоль линий, соединяющие эти частицы.
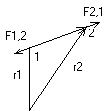
Различают силы внутренние, те которые действуют между частями системы и внешние, которые действуют на систему извне. Из III закона для внутренних сил следует:
1)
2)
1. ЗСИ
Nчастиц
Сложим подобные выражения для всех частиц системы
;
Изменение
импульса происходит под воздействием
внешних сил действ. на систему. Если
внешними силами можно пренебречь, то
импульс системы сохраняется
2. ЗСМИ
II закон для первой частицы:
умножим на радиус вектор:
Просуммируем:
Сумма производных =произведению суммы
;
момент
импульса
Изменения
момента импульса системы равно суме
моментов внешних сил, действующих на
систему. Если моментами внешних сил
можно пренебречь, то момент импульса
сохраняется
