4) Свойства параллельных проекций

4) Свойства параллельного проецирования

При параллельном проецировании сохраняются все свойства центрального проецирования, а также возникают следующие новые свойства.

1. Проекции параллельных прямых параллельны между собой, т.е., если а b, то a₁ b₁. Пусть отрезки АВ и DE параллельны (рис. 1.3), тогда проецирующие плоскости AA₁BB₁ и DD₁E₁E будут также параллельны. Следовательно, линии A₁B₁ и D₁E₁ пересечения этих плоскостей с П₁ будут параллельны.

2.Отношение отрезков, принадлежащих параллельным прямым или одной прямой, равно отношению проекций этих отрезков, т.е., если AB DE, то AB / DE =  A₁B₁ / D₁E₁

3. При параллельном перемещении плоскости проекций проекция фигуры не изменяется. Если П₁П₂, то A₁B₁C₁ = A₂B₂C₂ (рис.1.4).

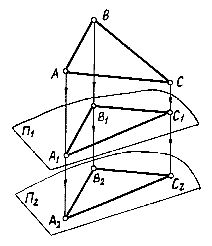Рис.1.4 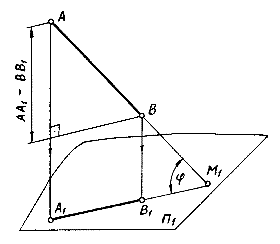Рис.1.5

9) Плоскости уровня

9) Плоскости уровня

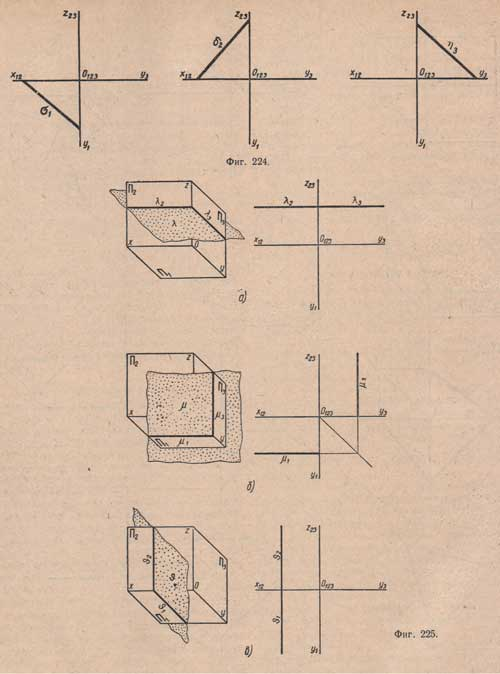
1. Плоскость λ параллельна плоскости П₁. Такую плоскость называют горизонтальной. Фронтальная и профильная проекции параллельны осям х и у

2. Плоскость μ параллельна плоскости П₂. Такую плоскость называют фронтальной. Горизонтальная и профильная проекции параллельны осям х и z. 3. Плоскость θ параллельна плоскости П₃. Такую плоскость называют профильной. Фронтальная и горизонтальная проекции параллельны осям z и у. Плоскости уровня называют также дважды проектирующими. Плоскости уровня принято изображать их проекциями. Особенность этих плоскостей состоит в том, что прямая, кривая или фигура, лежащие в этих плоскостях, проектируются на параллельную ей плоскость проекций в натуральную величину, а на две другие - отрезками, сливающимися с соответствующими проекциями плоскости.

Например: отрезок АВ расположен в горизонтальной плоскости λ; в этом случае его горизонтальная проекция равна натуральной величине отрезка.

10) Проецирующие плоскости

10) У проецируюих плоскостей все точки проецируются на проекцию прямой линии на той или иной координатной плоскости Самый простой вариант задания проецирующей плоскости - это задание двух точек с одинаковыми (попарно координатами), а третья произвольно. У горизонтально-проециующей плоскости вырожденная проекция будет на горизонтальную плоскость, У фронтально проециующей плоскости вырожденная проекция будет на фронтальную плоскость, У профильно проециующей - на профильную координатную плоскость, У все проецирующих плоскостей важное свойство в том, что все ее точки проецируются на одну прямую, которое эффективно используется при решении метрических задач. Упражнения: - Задать и изобразить фронтально-проециующую плоскость. - Задать и изобразить профильно-проециующую плоскость. Вопросы: - Может ли проецирующая плоскость фронтальной, горизонтальной или профильной плоскостью уровня? - Каким признаком определяется горизонтально-проецирующая плоскость? - Будет ли плоскость, лежащая в координатной плоскости xy, проецирующей? - Сколько следов (линий пересечения с координатными плоскостями) можетиметь, например, горизонтально-проецирующая плоскост?