4. Контрольные вопросы

1. Сформулируйте постановку задачи приближения функции по методу интерполяции.

2. Запишите интерполяционный многочлен Ньютона и интерполяционный многочлен Лагранжа первой степени.

3. Сформулируйте теорему об оценке погрешности интерполяции.

4. Какие преимущества имеет запись интерполяционного многочлена по формуле Ньютона перед формулой Лагранжа?

5. Объясните разницу между глобальной и кусочно-полиномиальной интерполяцией. Почему на практике чаще используется кусочно-полиномиальная интерполяция?

6. Дайте определение интерполяционного сплайна m-й степени.

7. Что такое дефект сплайна?

8. Запишите формулу сплайна первой степени с дефектом 1.

Практическая работа № 9 методы приближения и аппроксимации функций

1. Цель работы

На практике часто возникает необходимость найти функциональную зависимость между величинами x и y, которые получены в результате эксперимента. В отличие от интерполяции не требуется, чтобы аппроксимирующая функция проходила через все заданные точки, что особенно важно при аппроксимации данных, заведомо содержащих погрешности. Часто вид эмпирической зависимости известен, но числовые параметры неизвестны.

2. Основные сведения и примеры

Пример 9.1. Приближение функции по методу наименьших квадратов. Пусть функция задана таблицей своих значений:

x	-3	-1	0	1	3
y	-4	-0.8	1.6	2.3	1.5

Решение. Приблизим функцию многочленом 2-й степени . Для этого вычислим коэффициенты нормальной системы уравнений:

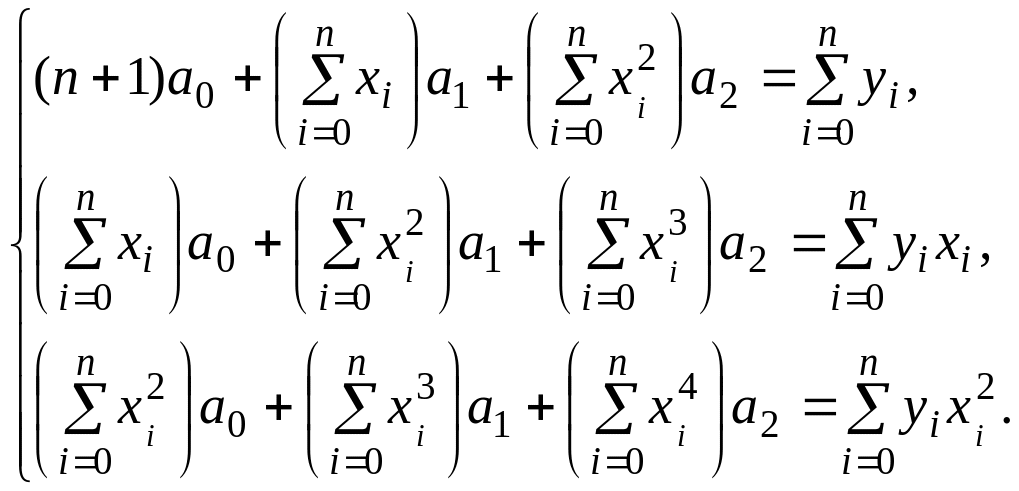
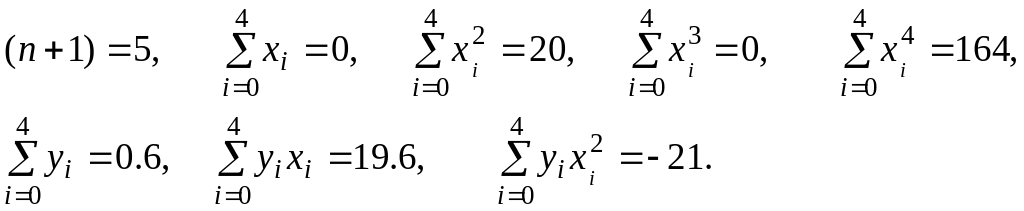
Составим нормальную систему наименьших квадратов, которая имеет вид:

Решение системы легко находится: . Таким образом, многочлен 2-й степени найден: .

Пример 9.2. Нахождение оптимальной степени многочлена¹.

Пример 9.3. Вывод нормальной системы уравнений для нахождения параметров эмпирической зависимости. Вывести систему уравнений для определения коэффициентов a и b функции , осуществляющей среднеквадратичную аппроксимацию заданной функции по n + 1 точкам.

Решение. Составим функцию и запишем для нее необходимое условие экстремума:

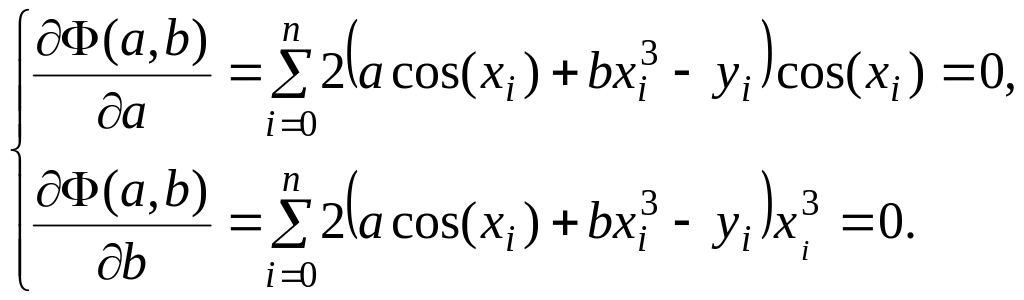
Тогда нормальная система примет вид:

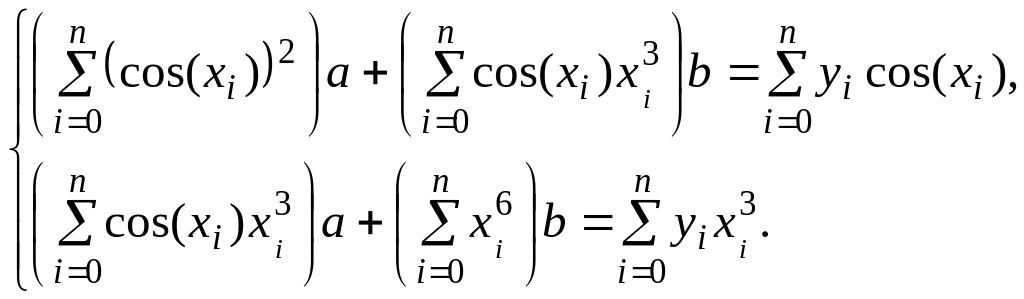
Получили линейную систему уравнений относительно неизвестных параметров, которая легко решается.

Реализация метода наименьших квадратов в MathCAD

Аппроксимация линейной функцией (линейная регрессия)

Критерием близости в методе наименьших квадратов является требование минимальности суммы квадратов отклонений от аппроксимирующей функции до экспериментальных точек: .

Читаем данные из файлов datax и datay:

_{x := READPRN( datax) y := READPRN( datay)}

При использовании MathCAD 2000 имя файла следует заключать в кавычки и записывать его по правилам MS DOS, например, _{READPRN("c:\mylib\datax.prn").}

Определяем количество прочитанных данных (число экспериментальных точек):

_{n := last ( x ) i := 0 .. n}

Используем встроенные функции slope и intercept для определения коэффициентов линейной регрессии (аппроксимация данных прямой линией). Функция slope определяет угловой коэффициент прямой, а функция intercept  – точку пересечения графика с вертикальной осью:

_{A := intercept ( x , y ) B := slope ( x , y )}

Определяем аппроксимирующую функцию:

_{f1(z) := A + B  z}

MathCAD 2000 предлагает для этих же целей использовать функцию line(x, y). Далее можно построить графики и вычислить стандартное отклонение:

Аппроксимация полиномами (полиномиальная регрессия)

Для этих целей служат встроенные функции regress и interp. Вводим степень полинома m. Функция regress является вспомогательной, она подготавливает данные, необходимые для работы функции interp. Вектор vs содержит, в том числе, и коэффициенты полинома:

_{vs:=regress(x,y,m)}

Функция interp возвращает значение полинома в точке z. Определив новую функцию f, мы получили возможность находить значение полинома в любой заданной точке:

_{f(z):=interp(vs,x,y,z) coeffs:=submatrix(vs,m,length(vs)–1,0,0)}

Провести полиномиальную регрессию можно и без использования функции regress. Для этого нужно определить коэффициенты нормальной системы и решить полученную систему уравнений, например, матричным методом:

Аппроксимация функциями специального вида (регрессия специального вида)

В MathCAD встроено несколько видов трехпараметрической регрессии. Используйте соответствующий вид регрессии, если хорошо представляете себе, какой зависимостью описывается массив данных. Помимо массива данных, требуется задать некоторые начальные значения параметров a, b, c в векторе g. Каждая из функций выдает вектор уточненных параметров a, b, c:

• expfit (x, y, g) – регрессия экспоненциальной функцией ;

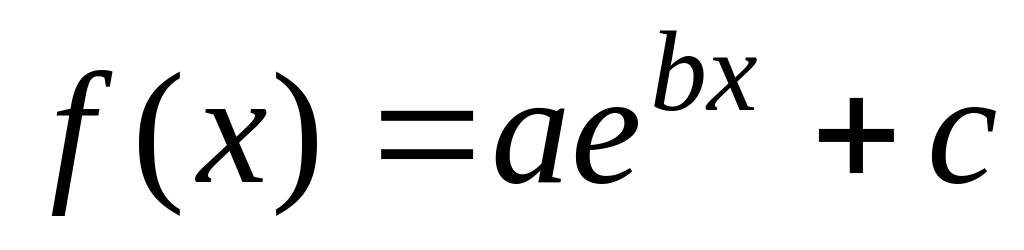• lgsfit (x, y, g) – регрессия логистической функцией ;

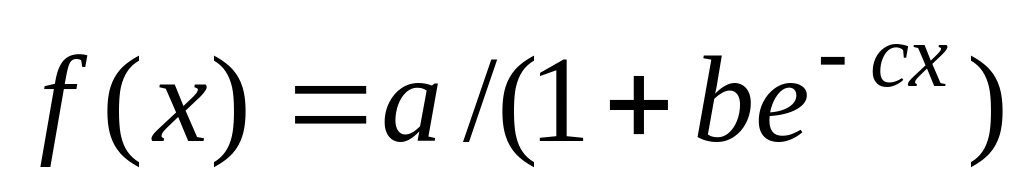• sinfit (x, y, g) – регрессия синусоидой ;

• pwfit (x, y, g) – регрессия степенной функцией ;

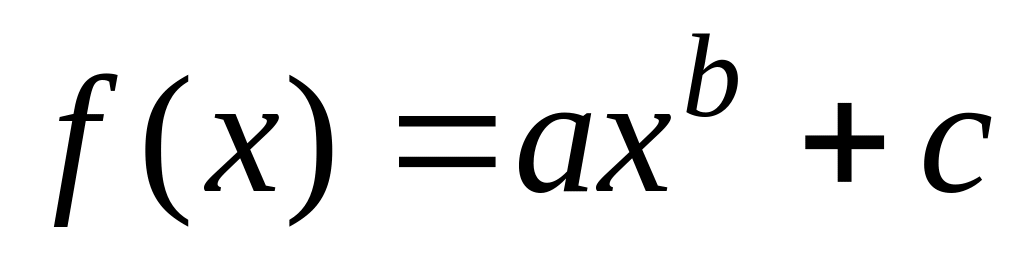• logfit (x, y, g) – регрессия логарифмической функцией ;

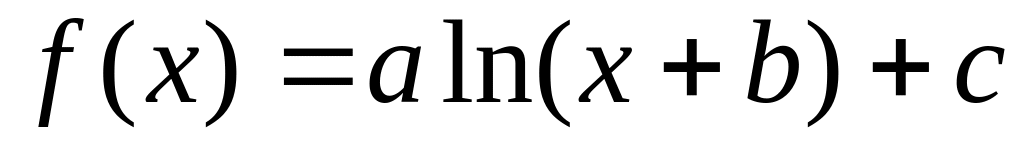• lnfit (x, y, g) – регрессия двухпараметрической логарифмической функцией .

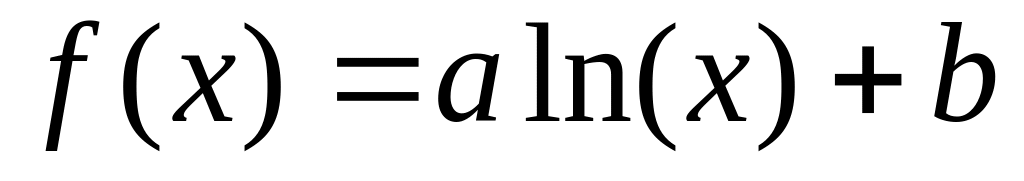Например,

Аппроксимация линейной комбинацией функций осуществляется функцией linfit ; аппроксимация функцией произвольного вида (регрессия общего вида) – функцией genfit.

В тех случаях, когда функциональная зависимость оказывается достаточно сложной, может оказаться, что самый простой способ нахождения коэффициентов – минимизация функционала Ф "в лоб".