Контрольная работа № 1 обработка табличных данных. Интерполяция

1. Цель работы

В данной работе рассматривается наиболее часто встречающийся вид точечной аппроксимации – интерполяция – нахождение значения таблично заданной функции в тех точках внутри данного интервала, где она не задана. Экстраполяция сводится к восстановлению функции в точках за пределами заданного интервала. В обоих случаях исходные данные могут быть получены как экспериментально (в этом случае принципиально отсутствуют промежуточные данные без дополнительных работ), так и расчетным путем по сложным зависимостям (в этом случае найти с помощью интерполяции значение сложной функции бывает проще, чем непосредственным вычислением по сложной формуле).

2. Основные сведения и примеры

Теоретический материал

Многочлен Лагранжа: ,

где – базисные многочлены Лагранжа.

При n = 1 по двухточечной таблице получаем формулу линейной интерполяции

,

а при n = 2 по трехточечной таблице получаем формулу квадратичной интерполяции

.

Оценить погрешность интерполяции в точке x из интервала можно величиной остаточного члена

,

где – максимальное значение (n +1)-й производной исходной функции f(x) на отрезке .

Первый интерполяционный многочлен Ньютона:

Часто вводят безразмерную переменную q, показывающую, сколько содержится шагов от базового узла x₀ до заданной точки x: q = (x – x₀)/h. Так как x - x_i = x₀ + qh – x₀ – ih = h (q – i), то приходим к первой интерполяционной формуле Ньютона:

.

Второй интерполяционный многочлен Ньютона:

Введя переменную q = (x – x_n) / h, получим вторую интерполяционную формулу Ньютона:

.

Погрешность интерполяции (величина остаточного члена) оценивается по формуле

.

В случае неравноотстоящих узлов для построения интерполяционных формул используют разделенные разности (разностные отношения). Через значения функции f(x₀), f(x₁), …, f(x_n) сначала определяют разделенные разности первого порядка:

На этих разностях базируются разделенные разности второго порядка:

………………………………………

Таким образом, если определены k-е разностные отношения , то (k+1)-е определяются через них равенством

.

Интерполяционная формула Ньютона для неравноотстоящих узлов имеет вид

Если функция n+1 раз на отрезке , содержащем узлы интерполяции x_i, i=0,1,...,n, дифференцируема, то для погрешности интерполяции (величины остаточного члена) справедлива оценка:

,

где – максимальное значение (n +1)-й производной исходной функции f(x) на отрезке ; ; .

Интерполяция в MathCAD

Локальная интерполяция

Простейшим случаем локальной интерполяции является линейная интерполяция, когда в качестве интерполяционной функции выбирается полином первой степени, то есть узловые точки соединяются прямой линией. Линейная интерполяция в MathCAD осуществляется с помощью встроенной функции linterp.

Пусть требуется провести линейную интерполяцию функции sin(x) на интервале [0..6], используя пять узлов интерполяции, и вычислить значения функции в четырех точках x_k:

_{k :=0..3 x k :=}

-0.5

1.111

2.333

4.574

Задаем интервал изменения x и число узловых точек:

_{x min := 0 x max := 6 n := 5}

Определяем шаг изменения x:

Вычисляем координаты узлов и значения функции в них:

_{i := 0 .. n - 1 x i := x min+ ih y i := sin(x i)}

Проводим линейную интерполяцию:

Вычислим значения интерполяционной функции в заданных точках и сравним их с точными значениями:

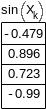
Интерполяция сплайнами

В настоящее время среди методов локальной интерполяции наибольшее распространение получила интерполяция сплайнами (от англ. spline – гибкая линейка). При этом строится интерполяционный полином третьей степени, проходящий через все заданные узлы и имеющий непрерывные первую и вторую производные. На каждом интервале интерполирующая функция является полиномом третьей степени:

,

и удовлетворяет условиям

. (8.1)

Если всего n узлов, то интервалов  n – 1. Значит, требуется определить 4(n – 1) неизвестных коэффициентов полиномов. Условие (8.1) дает нам n уравнений. Условие непрерывности функции и ее первых двух производных во внутренних узлах интервала дает дополнительно 3(n – 2) уравнений:

Всего имеем различных уравнений. Два недостающих уравнения можно получить, задавая условия на краях интервала одного из следующих видов:

1) (кубический сплайн дефекта 1);

2) (кубический сплайн дефекта 2);

3) (кубический сплайн дефекта 3).

Задавая различные условия на концах интервала, можно получить разные сплайны.

Решим задачу об интерполяции синуса с помощью сплайнов. Для этого воспользуемся встроенной функцией interp(VS,x,y,z). Переменные x и y задают координаты узловых точек, z является аргументом функции, VS определяет тип граничных условий на концах интервала.

Определим интерполяционные функции для трех типов кубического сплайна:

– вектор значений коэффициентов линейного сплайна, ;

– вектор значений коэффициентов квадратичного сплайна, ;

– вектор значений коэффициентов кубического сплайна, .

Вычисляем значения интерполяционных функций в заданных точках и сравниваем результаты с точными значениями:

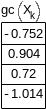
Обратите внимание, что результаты интерполяции различными типами кубических сплайнов практически не отличаются во внутренних точках интервала и совпадают с точными значениями функции. Вблизи краев интервала отличие становится более заметным, а при экстраполяции за пределы заданного интервала различные типы сплайнов дают существенно разные результаты. Для большей наглядности представим результаты линейной интерполяции и сплайн-интерполяции на графиках (рис. 8.1 - 8.4).

Убедимся в том, что первые и вторые производные сплайна непрерывны (рис. 8.5, 8.6). Но производные более высоких порядков уже не являются непрерывными.

Рис. 8.1

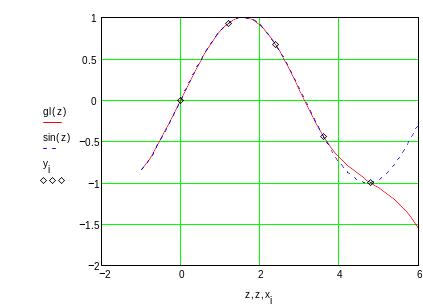
Рис. 8.2

Рис. 8.3

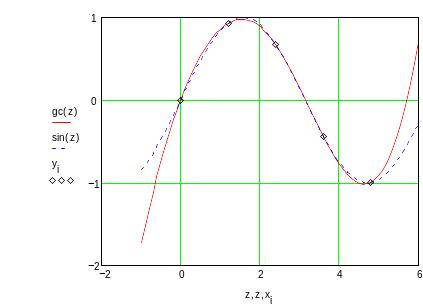
Рис. 8.4

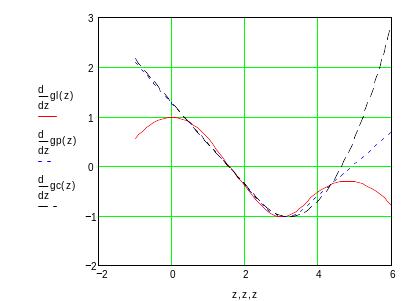
Рис. 8.5

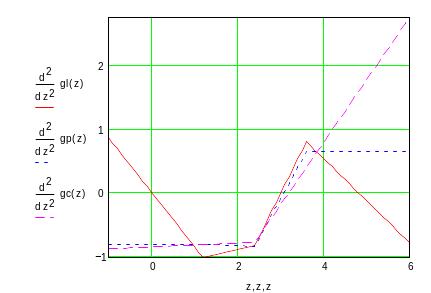
Рис. 8.6

Глобальная интерполяция

При глобальной интерполяции определяется единый полином для всего интервала. Если среди узлов {x_i,y_i} нет совпадающих, то такой полином будет единственным, и его степень не будет превышать n.

Запишем систему уравнений для определения коэффициентов полинома:

Определим матрицу коэффициентов системы уравнений:

Решим систему уравнений матричным методом:

Определим интерполяционный полином:

Представим результаты на графике (рис. 8.7).

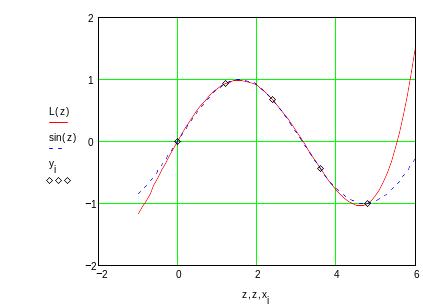
Рис. 8.7

Вычислим значения интерполяционного полинома в заданных точках и сравним их с точными значениями:

Коэффициенты интерполяционного полинома следующие:

Из-за накопления вычислительной погрешности (ошибок округления) при большом числе узлов (n>10) возможно резкое ухудшение результатов интерполяции. Кроме того, для целого ряда функций глобальная интерполяция полиномом вообще не дает удовлетворительного результата. Рассмотрим в качестве примера две такие функции. Для этих функций точность интерполяции с ростом числа узлов не увеличивается, а уменьшается. Первым примером является функция .

_{Построим для нее интерполяционный полином на интервале [–1;1], используя 9 точек:}

Представим результаты на графике (рис. 8.8).

Второй пример – функция _.

_{Найдем интерполяционный полином, используя заданные выше точки.}

Представим результаты на графике (рис. 8.9).

Рис. 8.8

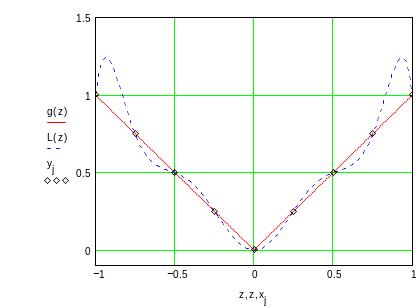
Рис. 8.9

Убедитесь самостоятельно, что при увеличении числа узлов интерполяции результаты интерполирования вблизи концов интервала ухудшаются.

Пример 8.1. Построить многочлен Лагранжа для таблично заданной функции

x	-1	0	1	2
y	4	2	0	1

Решение. Построим интерполяционный многочлен:

Пример 8.2. С помощью интерполяции многочленом Ньютона для равноотстоящих узлов найти y(2.05) для таблично заданной функции y.

Решение. Используем для интерполяции только три первые точки, а остальные используем для оценки погрешности. Следовательно, n = 2; h = =0.1; относительное значение аргумента q= (x – x₀)/h = 0.5. Воспользуемся первой интерполяционной формулой Ньютона для безразмерной переменной q, для чего предварительно составим таблицу конечных разностей:

x	y	y	2y	3y
2.0	0.0540	-0.0100	0.0015	-0.0002
2.1	0.0440	-0.0085	0.0013	0.0000
2.2	0.0355	-0.0072	0.0013	-0.0003
2.3	0.0283	-0.0059	0.0010	-0.0010
2.4	0.0224	-0.0049	0.0000	–
2.5	0.0175	-0.0049	–	–
2.6	0.0136	–	–	–

y(2.05) = 0.0540 + 0.5(–0.01) + 0.5(0.5 –1)0.0015/3! = 0.0488125.

Оценим погрешность найденного значения y. Из таблицы находим, что M₃ = 0.0010, тогда

.

Пример 8.3. Построить интерполяционный многочлен Ньютона по формуле неравноотстоящих узлов для таблично заданной функции из примера 8.1.

Решение. Составим таблицу разделенных разностей:

x	f(x)	f(xi ; xi+1)	f(xi ; xi+1 ; xi+2)	f(xi ; xi+1 ; xi+2; xi+3)
-1	4	-2	0	1/2
0	2
		-2
1	0		3/2
		1
2	1

Теперь запишем интерполяционный многочлен Ньютона:

Отметим, что в силу единственности интерполяционного многочлена мы получили тот же самый многочлен, что в примере 8.1.

Пример 8.4. Использование остаточного члена интерполяции. Пусть требуется составить таблицу функции на отрезке [1,10]. Какой величины должен быть шаг h, чтобы при линейной интерполяции значение функции восстанавливалось с погрешностью не большей ?

Решение. Запишем остаточный член при линейной интерполяции:

.

Так как , то . Тогда . Следовательно, .

Пример 8.5. Глобальная интерполяция функции Рунге¹.

Пример 8.6. Кусочно-линейная интерполяция функции Рунге.

Пример 8.7. Построение параболического сплайна. Пусть дан фрагмент таблицы значений функции:

x	-1	0	1
y	1.5	0.5	2.5

Требуется построить параболический сплайн дефекта 1.

Решение. Так как строится сплайн , то он будет представлен двумя полиномами 2-й степени:

Функция должна удовлетворять условиям:

, – это есть условие интерполяции;

  – это есть условие непрерывности первой производной.

Таким образом, получили 5 условий для нахождения 6 неизвестных. Два условия дополнительно накладывают на сплайн в граничных точках. Возьмем, например, дополнительное граничное условие следующего вида: . Тогда получим систему уравнений относительно неизвестных коэффициентов :

Эта система легко решается:

  .

Таким образом,