1.5 Текучесть и вязкость
Текучесть это свойство, означающее способность течь под влиянием самых малых сдвигающих усилий.
Вязкостью называется свойство жидкости оказывать сопротивление относительному сдвигу и скольжению соприкасающихся слоёв. Вязкость характеризует степень текучести жидкости или подвижности её частиц.
Все реальные жидкости обладают определённой вязкостью. Вязкость приводит к появлению сил внутреннего трения между смежными слоями, текущими с различными скоростями.
Пусть жидкость течёт вдоль плоской стены параллельными слоями. Тормозящее влияние стены приводит к тому, что разные слои будут иметь разные скорости (рис. 1.1). Рассмотрим слои А и В на расстоянии y друг от друга. Слой А движется со скоростью u, а слой В со скоростью (u + u).
Вследствие разности скоростей слой В по отношению к слою А движется со скоростью u и за каждую единицу времени сдвигается относительно слоя А на величину u, называемую абсолютным сдвигом. Отношение (u/y) есть градиент скорости или относительный сдвиг. При этом движении в результате внутреннего трения появляются касательные напряжения (сила трения на единицу площади) (тау). Аналогично сдвигу в твёрдых телах запишем зависимость между напряжением и деформацией:
=
×
.
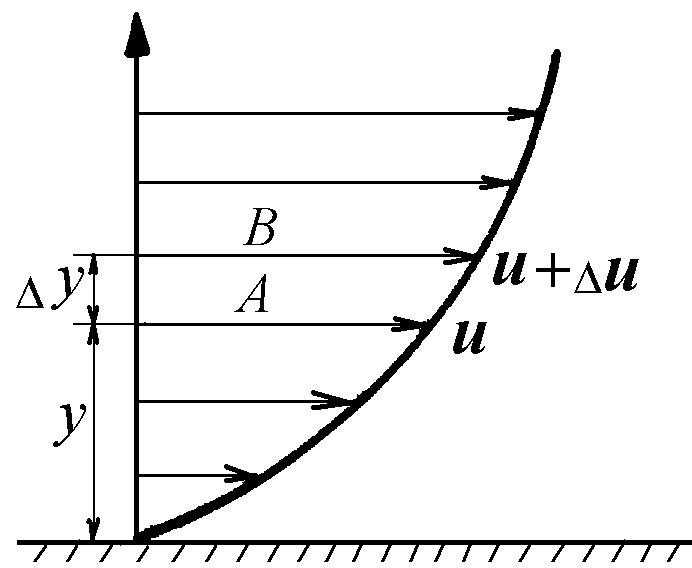
Рисунок 1 – Изменение скорости слоёв жидкости u при изменении расстояния y от твёрдой стенки
Если слои находятся бесконечно близко друг к другу, зависимость имеет вид:
=
×
.
(1.11)
Впервые это соотношение показал Ньютон, и оно носит название закон Ньютона.
Силы трения (сдвига) в жидкости не зависят от давления. Внутреннее трение прямо пропорционально площади соприкосновения трущихся слоёв и градиенту скорости по нормали и зависит от рода и состояния жидкости.
F = × .
Уравнение Ньютона имеет вид:
F = × × . (1.12)
Величина (эта) характеризует сопротивление жидкости сдвигу и называется коэффициентом динамической вязкости.
Для определения размерности коэффициента динамической вязкости выразим его из формулы (1.11):
=
;
=
= Па ×
с.
Физический смысл коэффициента динамической вязкости : динамический коэффициент вязкости равен силе, которая возникает на 1 м2 поверхности двух, перемещающихся друг относительно друга слоёв жидкости при градиенте скорости (du/dy) = 1.
Для капельных жидкостей с повышением температуры коэффициент динамической вязкости уменьшается, а для газов возрастает.
В расчётах чаще используют кинематический коэффициент вязкости (ню):
=
,
(1.13)
Коэффициент кинематической вязкости характеризует ускорение (замедление) частиц, вызванное силами вязкости.
Коэффициент кинематической вязкости капельных жидкостей при давлениях, встречающихся в большинстве случаев (до 200 ат) весьма мало зависит от давления, и этим изменением в гидравлических расчётах пренебрегают.
Коэффициент кинематической вязкости капельных жидкостей зависит от температуры. С увеличением температуры уменьшается.
Коэффициент кинематической вязкости газов зависит от температуры и давления, возрастая с увеличением температуры.