Тема 21 Уравнение Бернулли для потока конечных размеров. Гидравлический и пьезометрический уклоны

В случае плавно изменяющегося движения, при котором линии тока параллельны или почти параллельны, а кривизна струек незначительна, уравнение Бернулли, составленное для элементарной струйки, можно распространить на поток с поперечным сечением конечных размеров. Поток рассматривается при этом как совокупность элементарных струек, движущихся с различными скоростями. В таком потоке скорости в разных точках поперечного сечения различны, а скоростной напор, определяемый средней скоростью v, дополнен коэффициентом кинетической энергии (или коэффициентом Кориолиса) . Величина этого коэффициента отражает степень неравномерности распределения скоростей по сечению потока. Коэффициент равен отношению истинной кинетической энергии массы жидкости, протекающей через живое сечение, к кинетической энергии, вычисленной в предположении, что во всех точках живого сечения местные скорости равны средней скорости.

Обычно при прямолинейном турбулентном движении в трубах  = 1,03…1,1. Обычно при расчётах при турбулентном течении в трубах принимают коэффициент Кориолиса  равным 1,1 или 1. При прямолинейном ламинарном движении в трубах  = 2.

Уравнение Бернулли для установившегося движения невязкой несжимаемой жидкости в форме давлений имеет вид:

 × g × z + р +  ×  × = const, (21.1, а)

где  × g × z – гравитационное давление;

р – статическое давление;

 × – динамическое давление.

Для двух произвольных сечений 1-1 и 2-2 уравнение имеет вид:

 × g × z₁ + р₁ +  × ₁ × =  × g × z₂ + р₂ +  × ₂ × = const. (21.1, б)

Уравнение Бернулли для установившегося движения невязкой несжимаемой жидкости в форме напоров имеет вид:

z + +  × = Н = const, (21.2, а)

где z – удельная потенциальная энергия положения;

– удельная потенциальная энергия давления;

– удельная кинетическая энергия;

Н – полная удельная энергия потока.

Для двух произвольных сечений 1-1 и 2-2 уравнение имеет вид:

z₁ + + ₁ × = z₂ + + ₂ × = Н = const. (21.2, б)

С энергетической точки зрения уравнение Бернулли можно сформулировать так:

при установившемся движении невязкой несжимаемой жидкости вдоль потока сумма удельных энергий – потенциальной (положения и давления) и кинетической – есть величина постоянная.

Все члены уравнения Бернулли имеют линейную размерность и их можно интерпретировать как высоты:

z – геометрическая высота, то есть высота положения рассматриваемой точки пространства с жидкостью (центра тяжести сечения) над горизонтальной плоскостью сравнения x0y;

– высота давления. Если в уравнении р – избыточное давление, то величина

= называется пьезометрической высотой;

 × – скоростная (или динамическая) высота.

Н – полная высота в данном сечении потока.

Таким образом, геометрический смысл уравнения Бернулли можно сформулировать так:

при установившемся движении невязкой несжимаемой жидкости вдоль потока сумма высот – положения, давления (или пьезометрической) и скоростной – есть величина постоянная.

Уравнение Бернулли для установившегося движения вязкой несжимаемой жидкости между двумя сечениями, в которых движение является плавно изменяющимся, имеет вид:

 в форме давлений

 × g × z₁ + р₁ +  × ₁ × =  × g × z₂ + р₂ +  × ₂× + р, (21.3)

где р – потери давления на участке между рассматриваемыми сечениями;

 в форме напоров

z₁ + + ₁× = z₂ + + ₂ × + h_пот, (21.4)

где h_пот – потери напора на участке между рассматриваемыми сечениями.

Для потока жидкости сумма удельной потенциальной и удельной кинетической энергии

Н = (21.5)

называется гидродинамическим (или полным) напором.

При движении вязкой жидкости линия удельной энергии (напорная линия) не горизонтальна, как при движении невязкой жидкости, а представляет собой наклонную линию, так как удельная энергия потока (гидродинамический напор) Е = Н = при движении вязкой жидкости уменьшается в направлении движения.

Энергетический смысл уравнения Бернулли для потока вязкой жидкости:

удельная энергия потока в предыдущем сечении всегда больше чем в последующем на величину потерь удельной энергии.

Геометрический смысл уравнения Бернулли для потока вязкой жидкости:

полная высота в предыдущем сечении всегда больше чем в последующем на высоту потерь.

Гидравлическим уклоном i называется отношение потерь напора h_тр к длине участка l, на котором эти потери происходят:

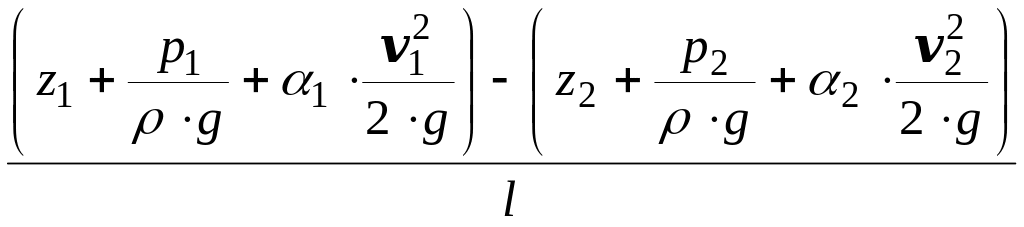
i = =  0. (21.6, а)

В общем виде

i =  =  =  0. (21.6, б)

Так как приращение dH всегда является отрицательным (напор уменьшается вдоль движения), то гидравлический уклон всегда положителен.

Удельная потенциальная энергия (пьезометрический напор) в направлении движения может, и уменьшатся, и увеличиваться, в зависимости от конкретных условий.

Пьезометрическим уклоном i_п называется отнесённое к единице длины изменение пьезометрического напора или изменение отметок пьезометрической линии. В общем случае

i_п = 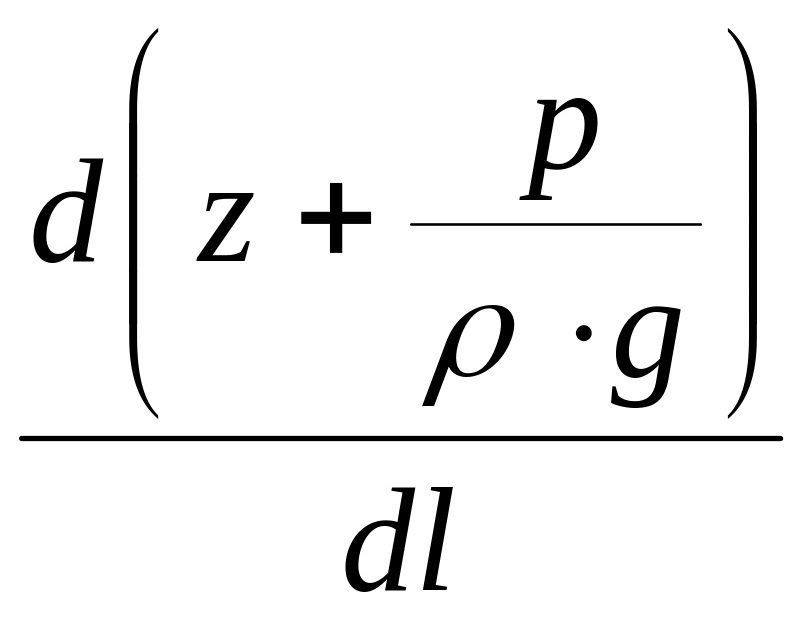 . (21.7, а)

Для двух сечений имеем

i_п = 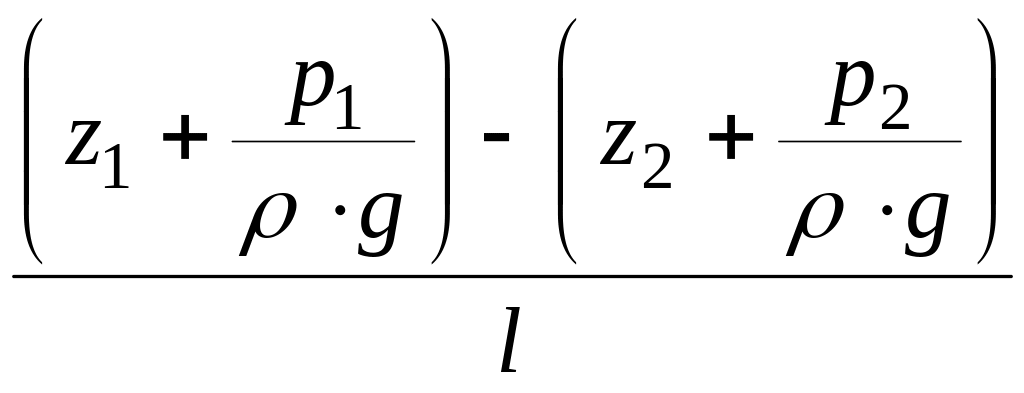. (21.7, б)

Пьезометрический уклон может быть положительным, отрицательным и равным нулю. Пьезометрический уклон считается положительным, если по течению пьезометрическая линия понижается.