§9. Выпуклость и вогнутость. Точки перегиба
Пусть функция
определена и непрерывна на интервале
и
пусть
и
– произвольные точки этого интервала,
удовлетворяющие неравенству:
.
Проведём через
точки
прямую (секущую).
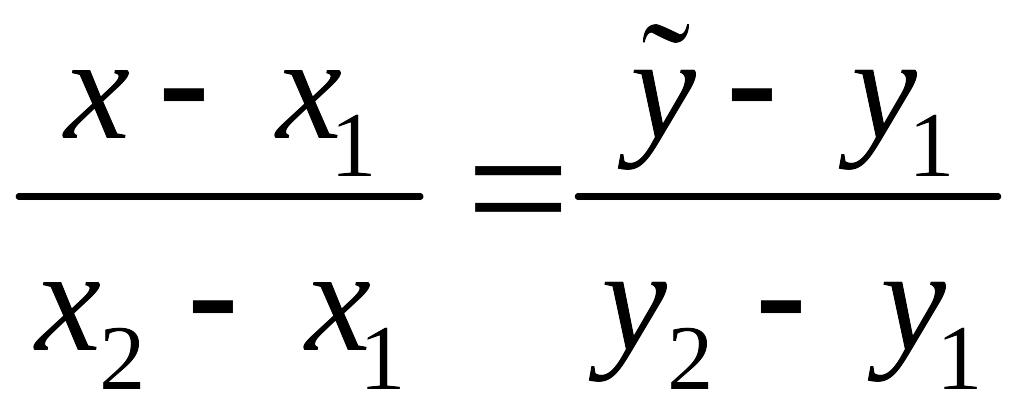. (1)
Обозначили
– ординату этой прямой, чтобы не путать
её с ординатой прямой
.
Так что
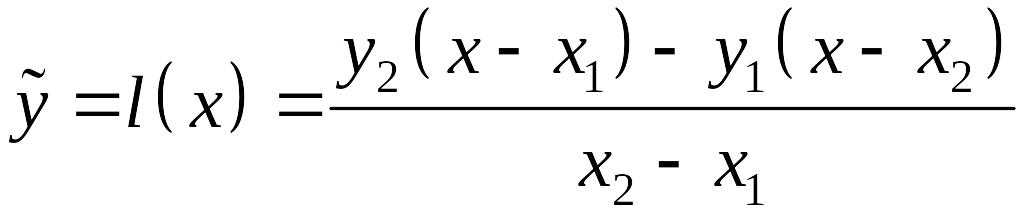. (1')
Определение 1. Функция называется выпуклой на интервале , если для любых точек , этого интервала выполняется неравенство
,
(2)
где
– произвольная
точка интервала
.
Аналогично, если
,
(3)
то функция вогнутая на интервале .
y
Геометрически выпуклость кривой означает, что любая точка хорды не выше точки кривой (см. рис.).
Если функция
– линейная,
то
,
то есть она одновременно выпуклая и
вогнутая.
Замечание 1. Если неравенства (2) и (3) строгие, то функция называется строго выпуклой или строго вогнутой.
Определение 2. Пусть функция определена и непрерывна в некоторой окрестности точки х0. Точка х0 называется точкой перегиба функции , если она является одновременно концом интервала строгой выпуклости и началом интервала строгой вогнутости или наоборот.
Точки перегиба
графика кривой отделяют выпуклую часть
кривой от вогнутой или вогнутую от
выпуклой (см. рис.).
y
Теорема 1
(достаточное условие выпуклости-вогнутости).
Пусть функция
определена и дважды дифференцируема
на интервале
.
Тогда, если
,
то функция строго выпуклая на
;
если
,
то – строго вогнутая.
Доказательство:
Пусть
.
Тогда
.
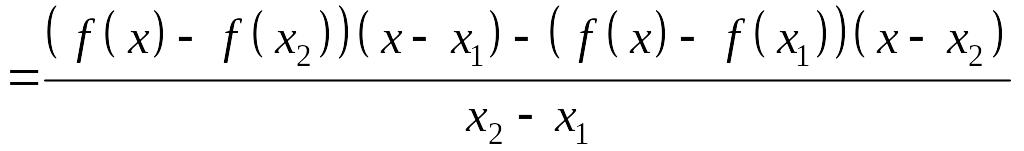(4)
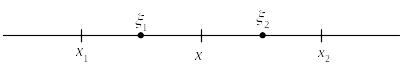
Согласно теореме Лагранжа
. (5)
Подставляя (5) в (4), получим
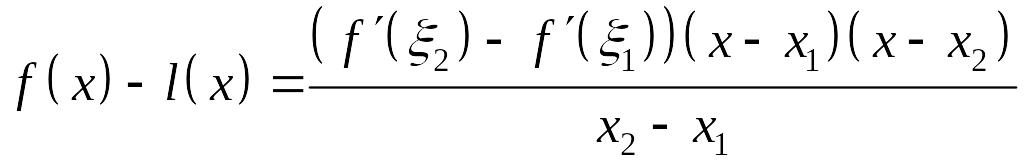. (6)
Применим теорему
Лагранжа к функции
на отрезке
. (7)
Подставляя (6) в (7), получим
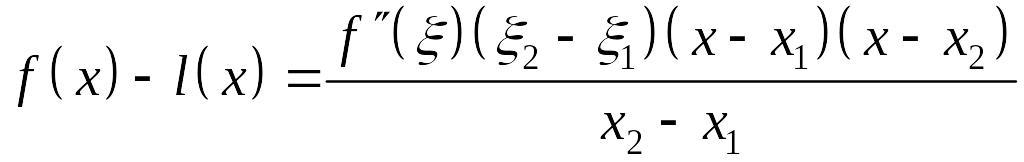. (8)
Из (8) видим, что
при
или
,
то есть функция
– строго
выпуклая. При
,
то есть функция
– строго
вогнутая. Теорема доказана.
Пример 1.
–
функция
всюду вогнутая.
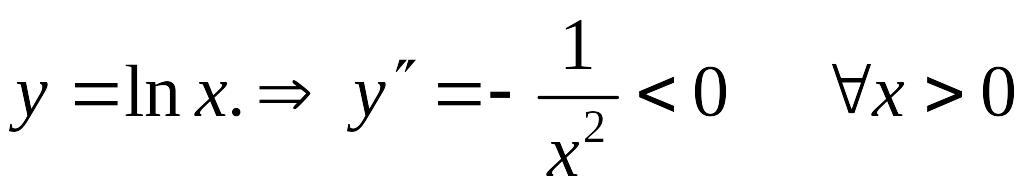– функция всюду
выпуклая.
Замечание 1.
Условия
теоремы 1 достаточные, они не являются
необходимыми, например,
всюду вогнутая, однако
.
Теорема 2
(необходимое условие точки перегиба).
Если функция
дважды
непрерывно дифференцируется в окрестности
точки х0,
а точка х0
является
точкой перегиба, то
.