§8. Исследование поведения функции. Интервалы монотонности, точки экстремума

Достаточное условие монотонности функции даёт теорема 1 §3, то есть если функция дифференцируемая, то решая неравенства и , найдём интервалы монотонности функции. Теорема Ферма даёт необходимое условие экстремума для дифференцируемой функции.

Заметим, что функция, непрерывная в точке , но не дифференцируемая в ней, может достигать экстремума. Например, функции достигают в точке минимума, но не дифференцируемые в этой точке. Даже разрывная в точке функция может достигать в этой точке экстремума. Например, функция

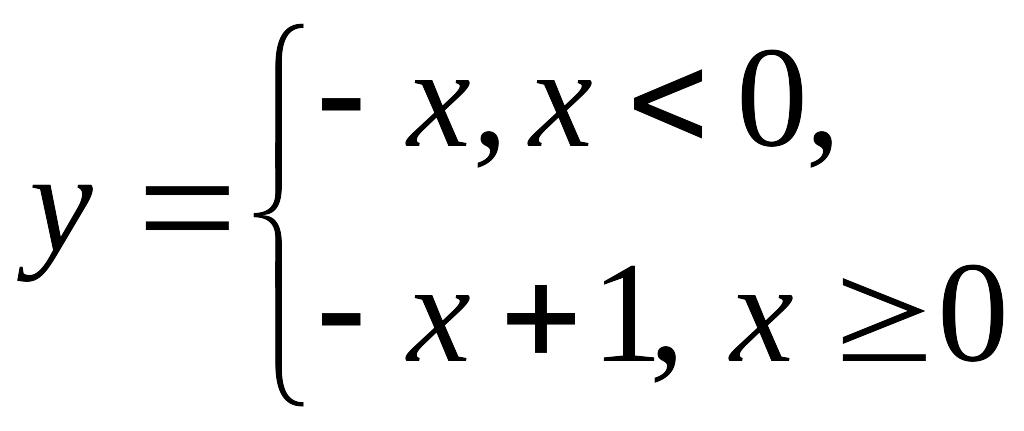
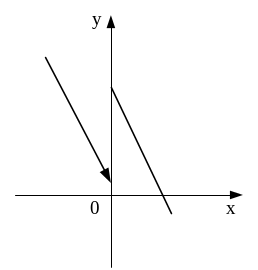
достигает в нуле максимума (см. рис.).

Из теоремы Ферма и приведённых примеров следует, что точки, в которых производная обращается в нуль или не существует (их называют критическими), – это точки возможного экстремума. Чтобы убедиться, достигается ли на самом деле в этих точках экстремум, следует воспользоваться достаточным условием.

Теорема 1 (достаточное условие экстремума для непрерывной функции). Пусть функция непрерывна в точке , дифференцируема в некоторой окрестности этой точки за исключением, быть может, самой точки . Тогда если при переходе через точку слева направо знак производной : а) меняется с + на –, то функция достигает в точке максимума; б) меняется с – на + – минимума; в) не меняется – экстремума нет.

Доказательство. Пусть или – произвольный отрезок из окрестности точки _. Функция удовлетворяет условию теоремы Лагранжа на этих отрезках, то есть

, (1)

или .

Рассмотрим случай а). Если , то и правая часть (1) отрицательна, то есть . Если , то и снова правая часть (1) отрицательная, то есть . Итак, для любого из окрестности точки имеем , что означает максимум в точке . Случай а) доказан. Случаи б) и в) доказываются аналогично. Теорема доказана.

Пример 1. Найти интервалы монотонности и экстремум функции .

Решение. Функция определена и непрерывна на всей числовой оси. Найдём критические точки

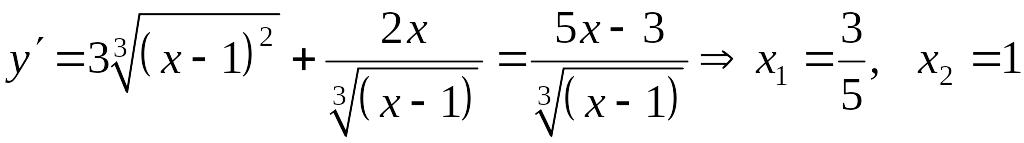 – критические точки. Они разбивают область определения функции на три интервала: 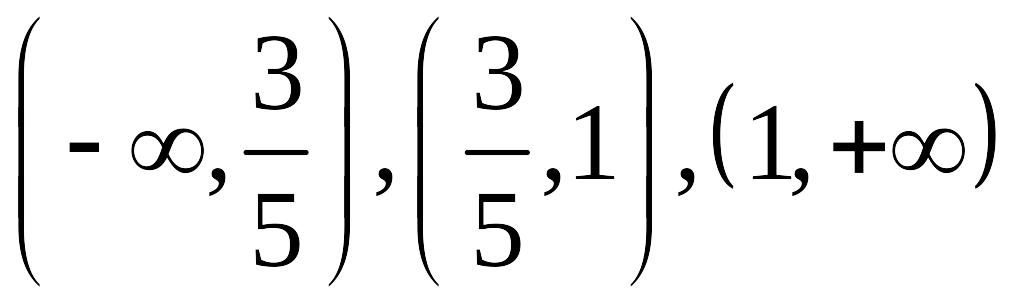, (см. рис.).

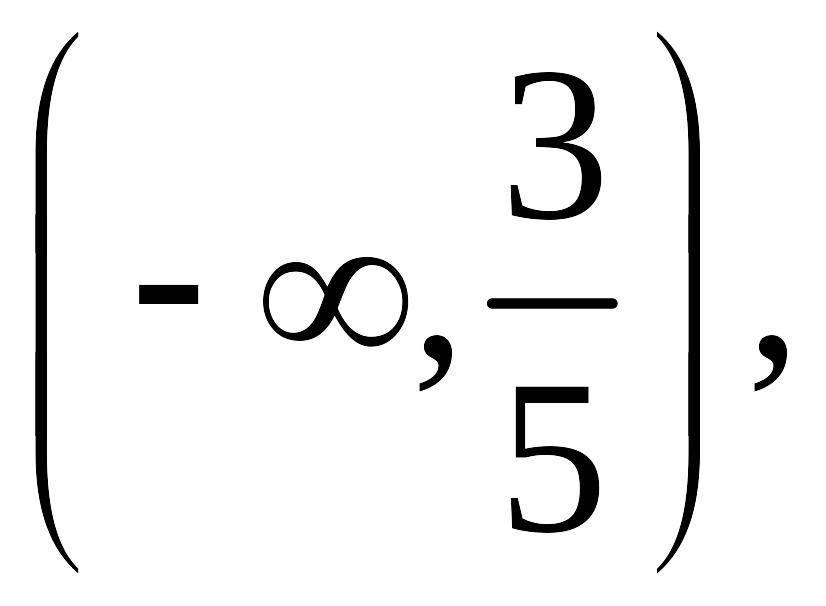
При этом производная положительна на первом и третьем интервале, а отрицательна на втором. Следовательно, функция возрастает на интервалах и убывает на интервале .

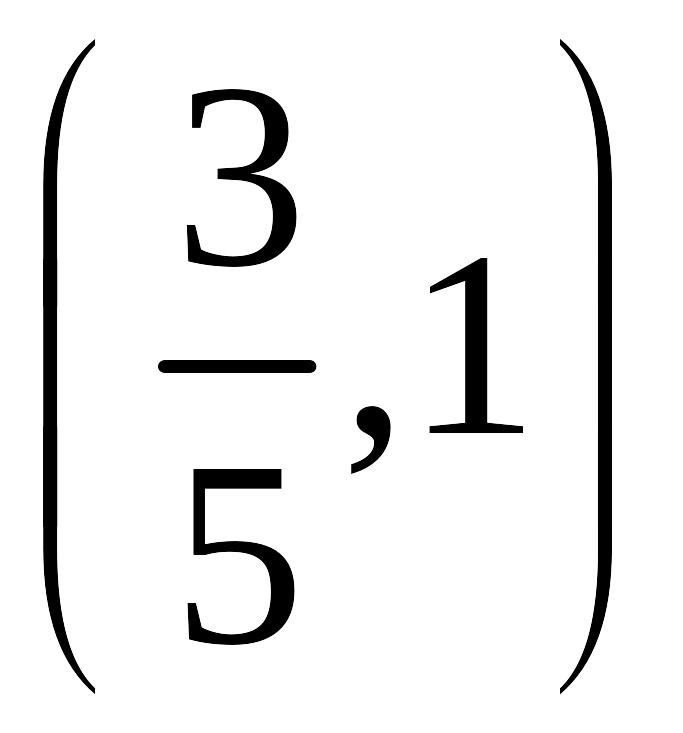Так как в меняет знак с + на –, то, согласно теореме 1, в этой точке достигает максимума, 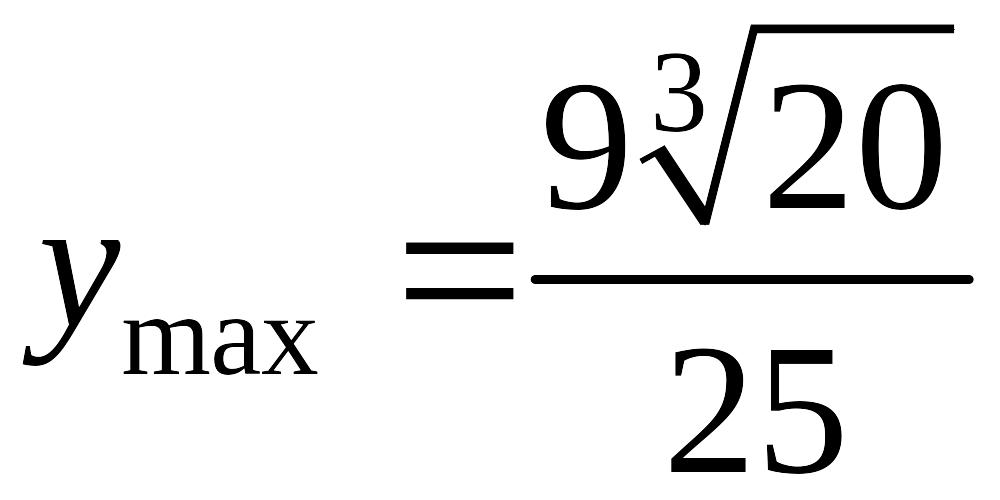. Аналогично в точке – минимума, .

Если функция дважды дифференцируема в критической точке, то можно дать второй достаточный признак существования экстремума.

Теорема 2. Если функция имеет в некоторой окрестности точки вторую производную, а , то достигает в точке максимума, если . Достигает минимума, если .

Доказательство. Из существования следует непрерывность и в окрестности точки . Пусть , тогда функция возрастает в окрестности точки . Поскольку , то меняет знак с – на +. А это, согласно теореме 1, означает минимум функции в точке . Аналогично доказывается случай, когда . Теорема доказана.

Пример 2. Убедиться, что функция примера 1 достигает в точке максимума.

Решение. .

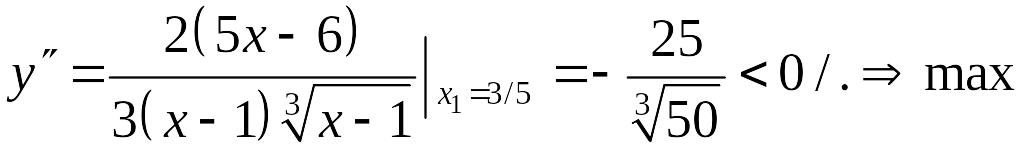Замечание. Если , то для выяснения существует ли экстремум можно воспользоваться формулой Тейлора:

.

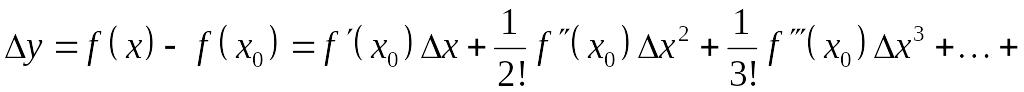
Пример 3. Исследовать на экстремум функцию

в точке .

Решение. ,

,

,

,

.

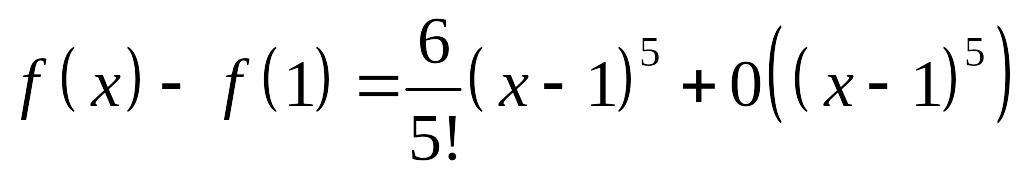. (2)

(2) – формула Тейлора.

Если взять достаточно малую окрестность точки , то знак правой части (2) будет определяться только первым слагаемым. Но его знак не сохраняется ни в какой окрестности точки . Следовательно, функция не имеет экстремума в точке .