§7. Примеры разложений по формуле Тейлора. Ряд Тейлора

Отметим, что при формула Тейлора (9) §6 совпадает с формулой Лагранжа.

Если , то из (9) §6 получим

, (1)

где Формулу (1) называют формулой Маклорена.

Если первое слагаемое формулы Тейлора (9) §6 перенести в левую часть и учесть, что

а , то её можно записать так:

. (2)

Рассмотрим несколько частных случаев разложения по формуле Тейлора или Маклорена.

Пример 1. Разложить по формуле Маклорена функцию .

Решение. Поскольку то из (1) получим

. (3)

Докажем, что остаточный член при Так как от не зависит и при любом конечном является ограниченной величиной, то достаточно показать, что последовательность сходится к нулю при любом конечном . Действительно,

. (4)

Из (4) видно, что при последовательность монотонно убывает. Но монотонно ограниченная последовательность сходится. Пусть тогда из (4) получим

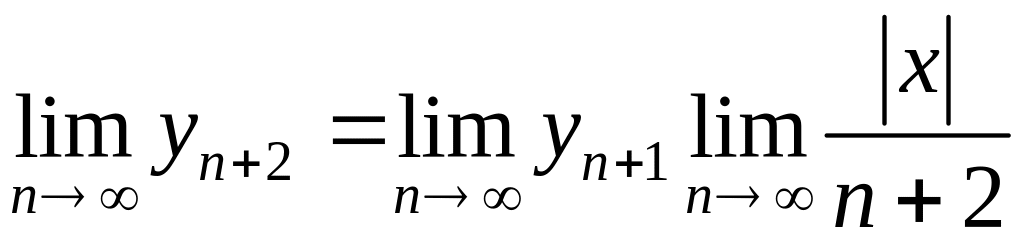или .

Итак, при

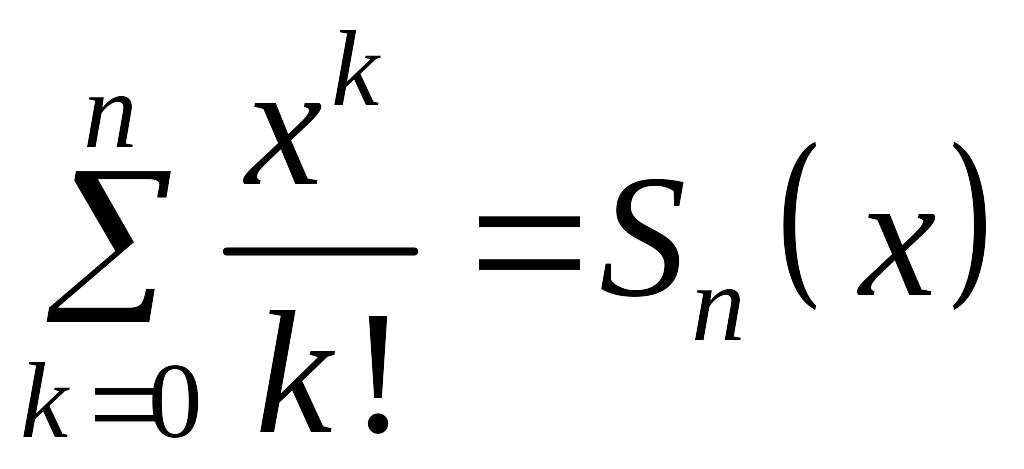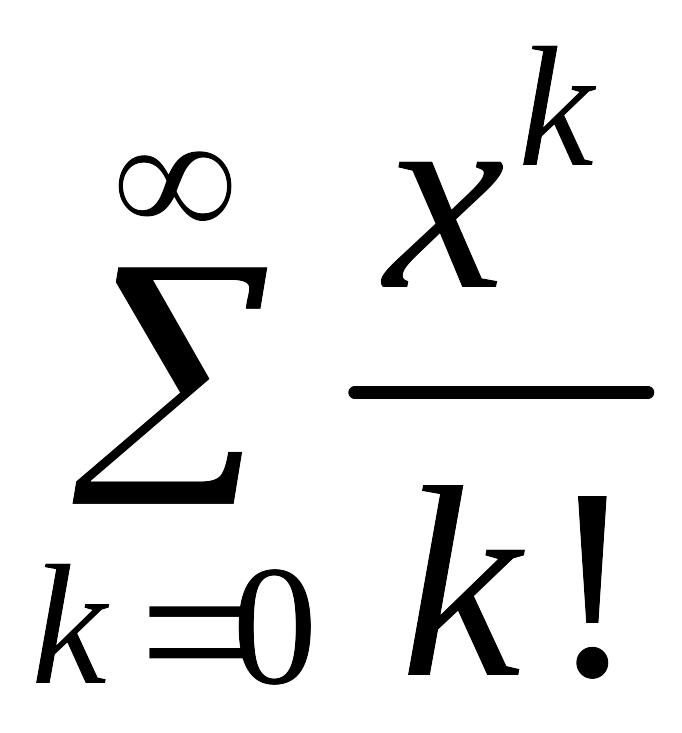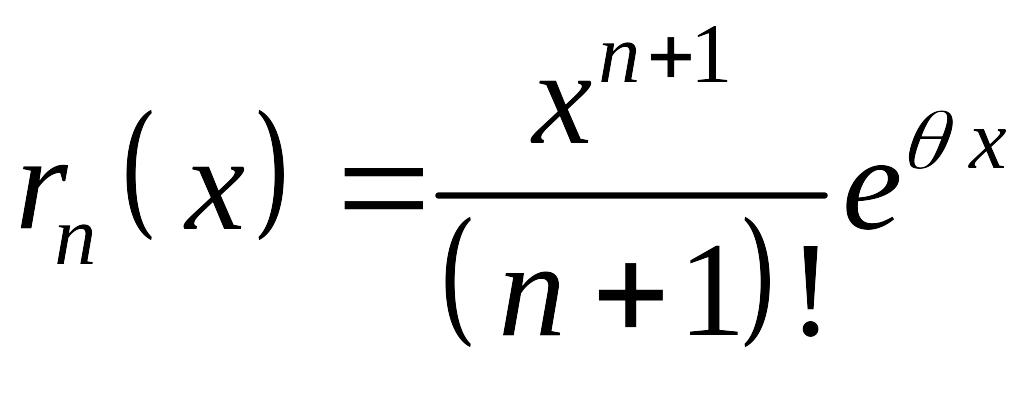Из (3) видно, что – частичная сумма степенного ряда , а остаточный член можно рассматривать как n-й остаток ряда. Поскольку при , то это означает, что степенной ряд сходится, и его сумма , то есть

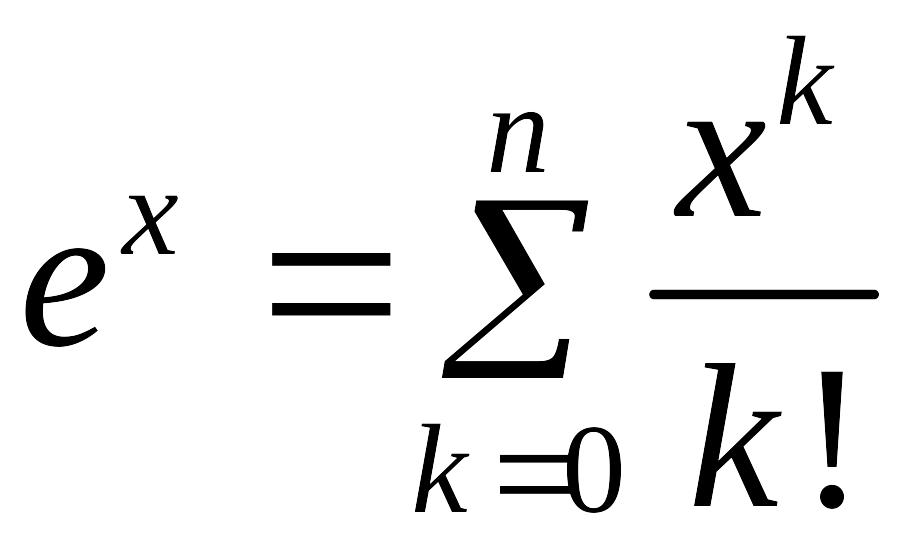. (5)

Степенной ряд 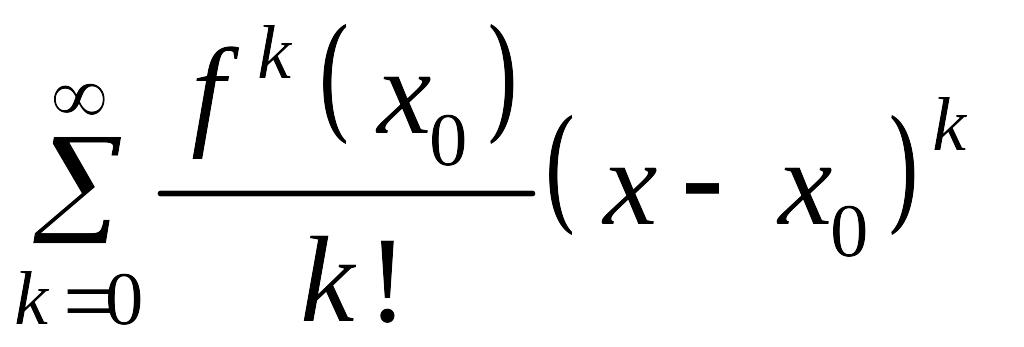называется рядом Тейлора (при рядом Маклорена) для функции вне зависимости от того, сходится он к или нет. Если он сходится к ,то говорят, что функция разлагается в ряд Тейлора. Например, функция разлагается в ряд Тейлора (5). Однако не любая бесконечное число раз дифференцируемая в точке функция разлагается в ряд Тейлора. Можно убедиться, что функция 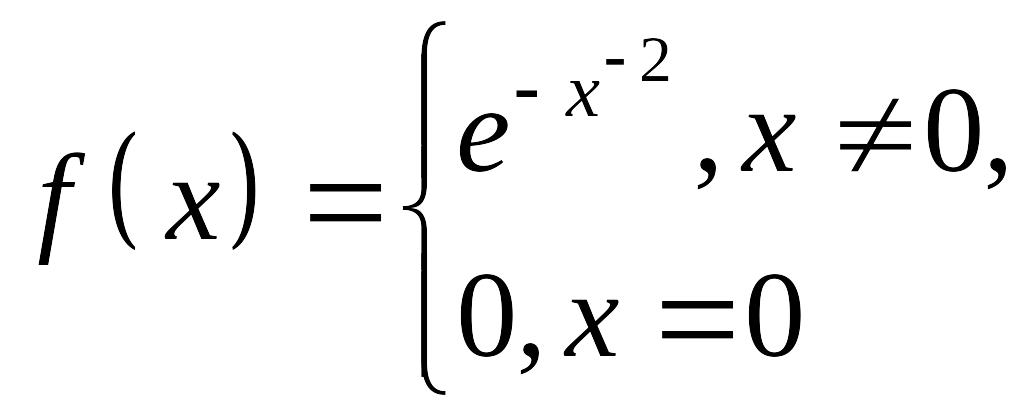бесконечное число раз дифференцируема в точке , но все её производные в этой точке равны нулю. Поэтому она не разлагается в ряд Маклорена.

С другой стороны, всякий степенной ряд , сходящийся к сумме в некоторой окрестности точки , является рядом Тейлора для своей суммы . Действительно, если

,

то .

То есть коэффициент С_к степенного ряда определяется по формуле

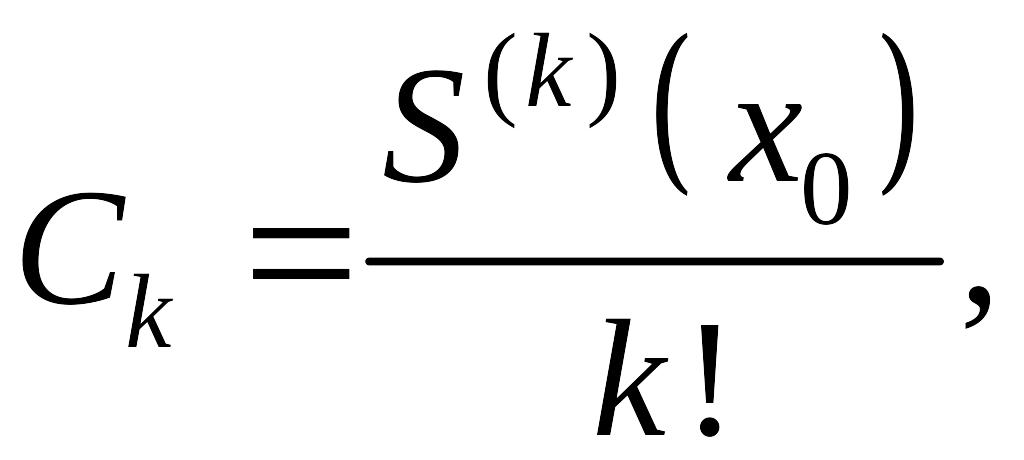
а это и означает, что степенной ряд является рядом Тейлора для своей суммы

Пример 2. Разложить в ряд Тейлора функции

Решение. Так как (5) сходится на всей числовой оси, то имеем

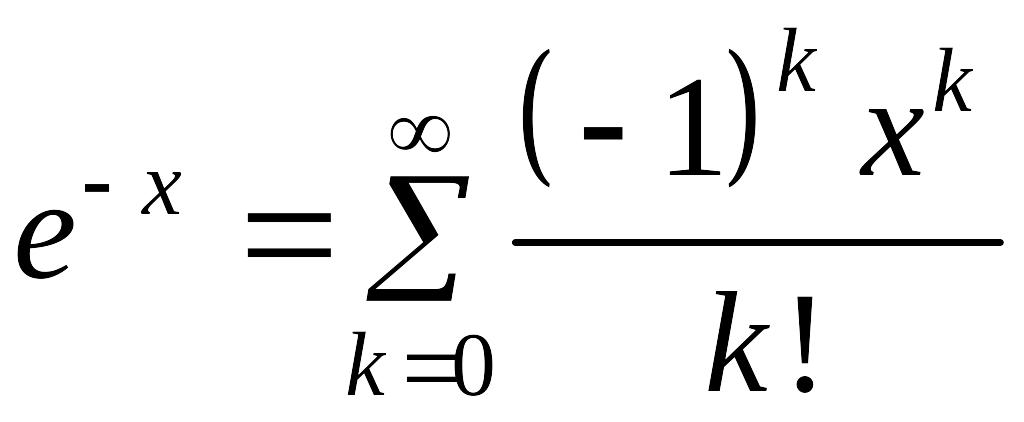. (6)

Поскольку сходящиеся ряды можно почленно складывать и умножать на число, то имеем

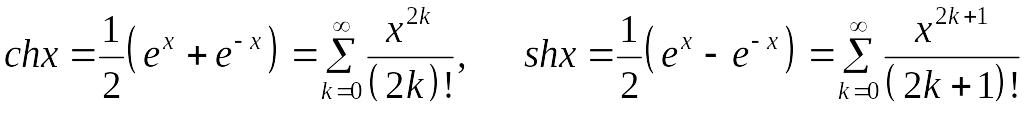. (7)

Пример 3. Разложить по формуле Маклорена функцию .

Решение. Поскольку 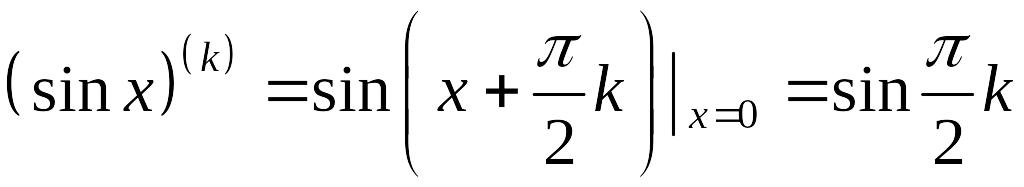, то из (1) получим

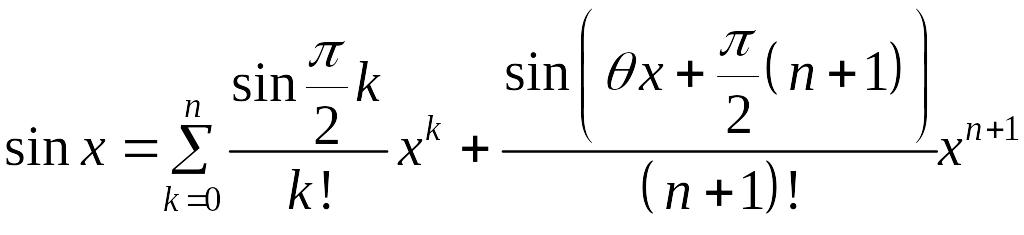. (8)

Как и в примере 1, можно доказать, что остаточный член формулы Маклорена

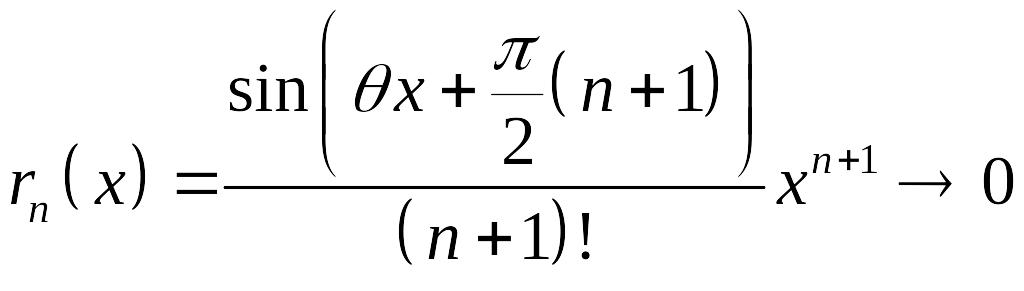
при для любого , то есть функция разлагается в ряд Маклорена

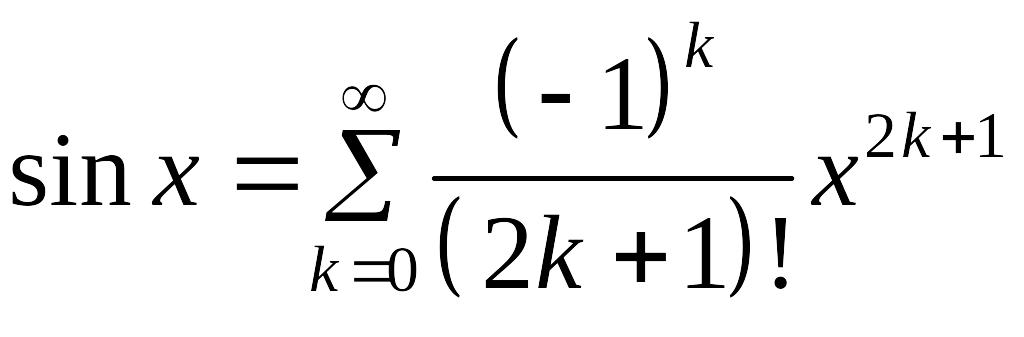. (9)

Упражнение. Доказать, что функция разлагается в ряд Маклорена на всей числовой оси, причём

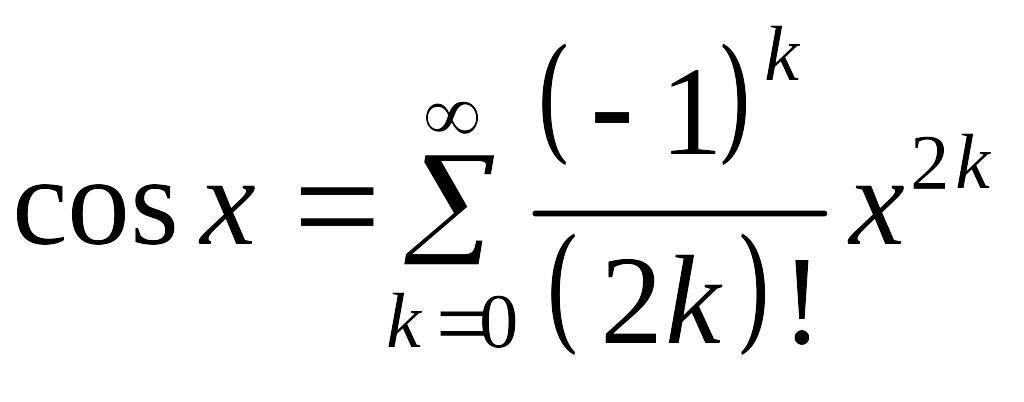. (10)

Пример 4. Разложить по формуле Маклорена функцию

Решение. Если , то получим бином Ньютона. Пусть , тогда

.

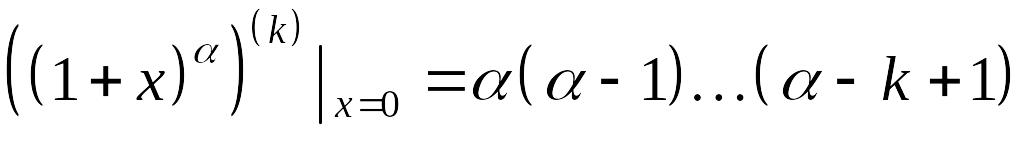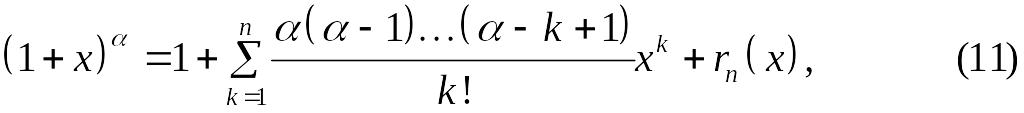
где

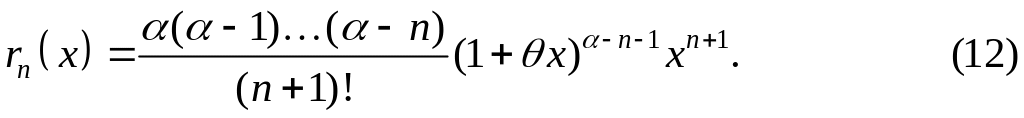
Можно убедиться, что остаточный член (12) при стремится к нулю, при , то есть из (11) получится разложение функции

в ряд Маклорена

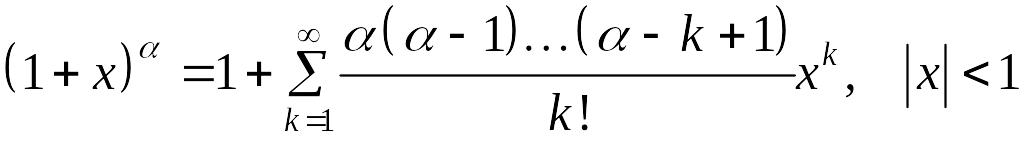. (13)

Аналогично можно найти разложение в ряд Маклорена функции

. (14)