§5. Формула Тейлора для многочлена. Бином Ньютона

Рассмотрим многочлен -й степени

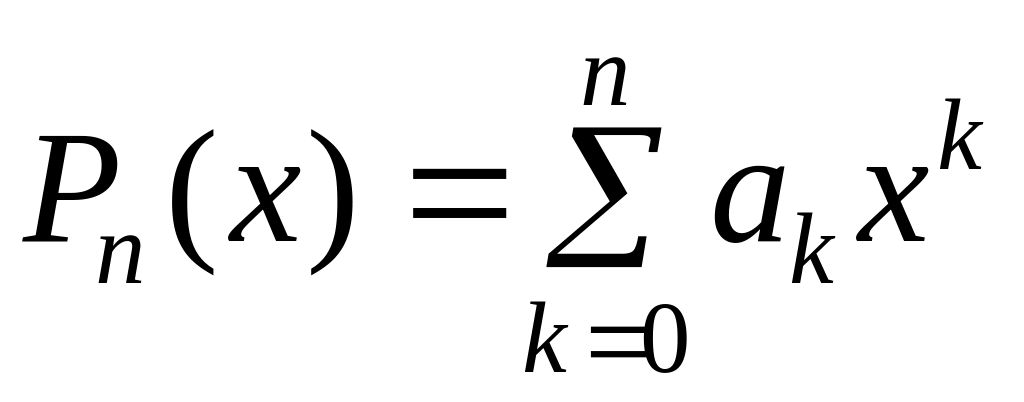. (1)

Представим этот многочлен следующим образом:

. (2)

Неизвестные коэффициенты найдём следующим образом. Продифференцируем (2) раз. Получим

(3)

…………………………………………………………….

Полагая в (2) и (3) , найдём:

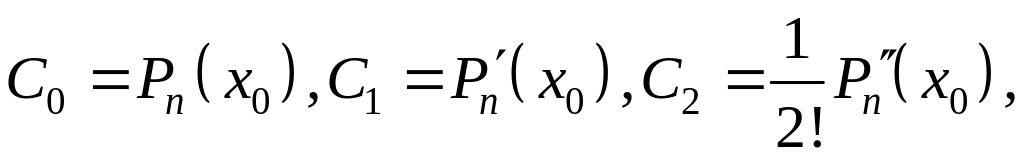
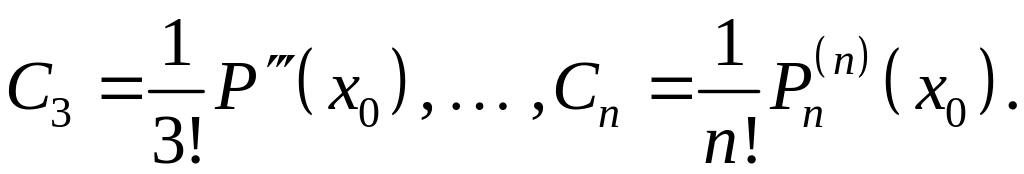
Ясно, что

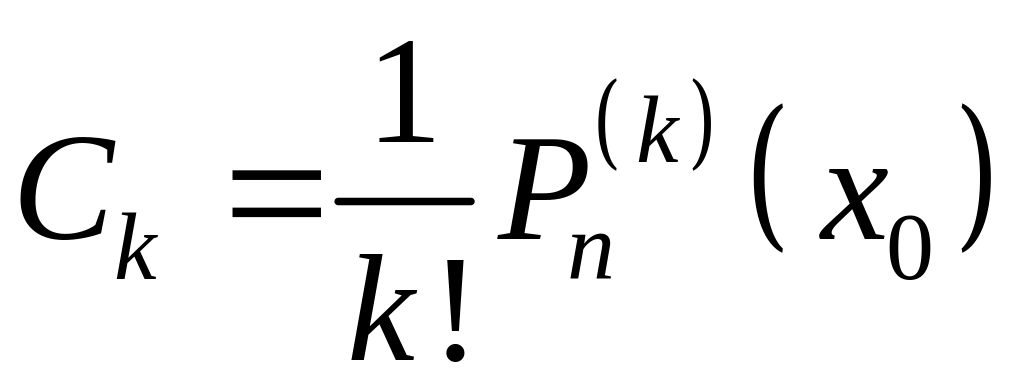. (4)

Таким образом, многочлен (2) примет вид

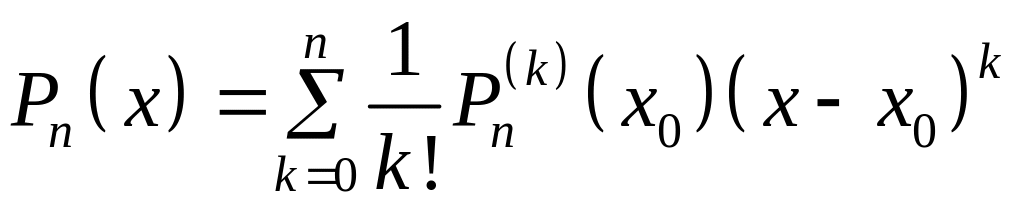. (5)

Многочлен (5) называют многочленом Тейлора. Его коэффициенты определяются соответствующей производной многочлена в точке . Очевидно, что всякий многочлен является многочленом Тейлора и задав значения многочлена и его производных в некоторой точке, мы определим и сам многочлен.

Рассмотрим частный случай

.

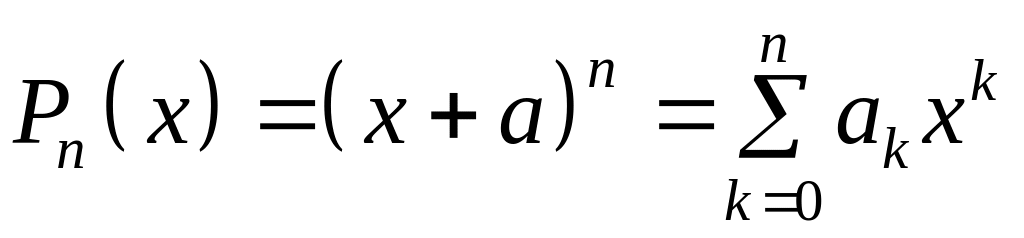Коэффициенты найдём по формуле (4) при .

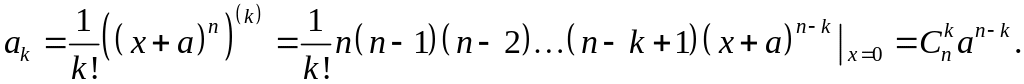
Таким образом, мы получили формулу бинома Ньютона.

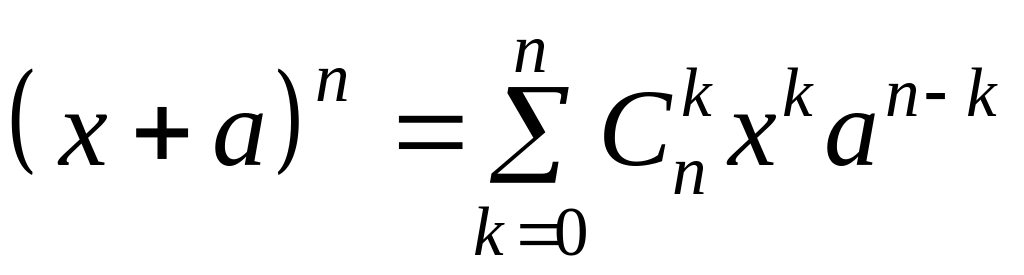. (6)

§6. Формула Тейлора для функции

Пусть функция дифференцируема раз в окрестности точки . Запишем для неё многочлен Тейлора

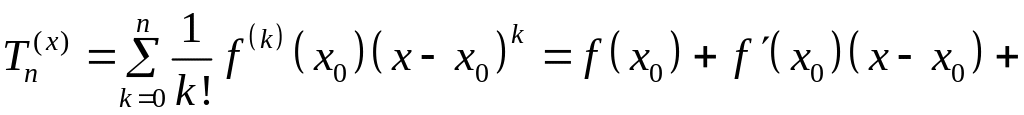
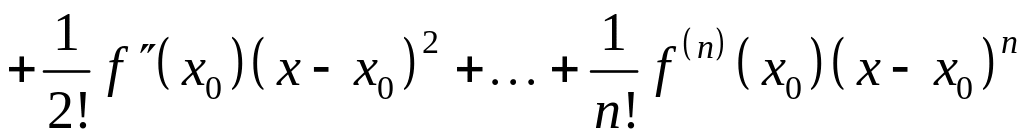. (1)

Как видно из (1) значение функции и всех её производных в точке совпадает со значением и производными многочлена Тейлора

. (2)

Однако, в точках функция может не совпадать с

многочленом Тейлора. Поэтому положим

. (3)

Величину называют остаточным членом. Из (3) с учётом (2) получим

. (4)

Докажем, что остаточный член является бесконечно малой высшего порядка малости по сравнению с , то есть

или .

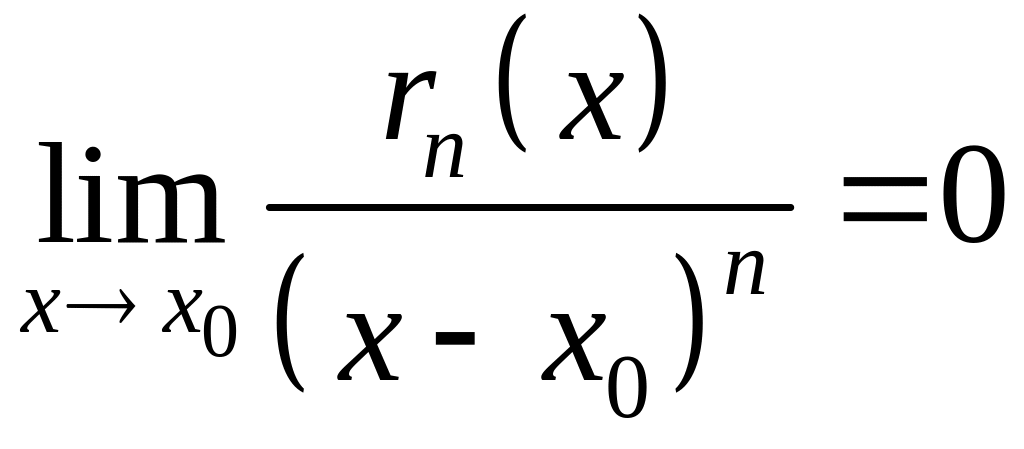Применяя раз правило Лопиталя и учитывая (4), найдём:

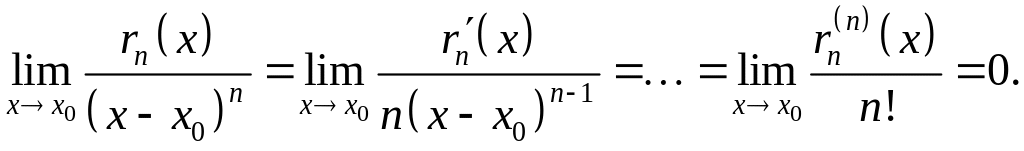
Что и требовалось доказать.

Формулу

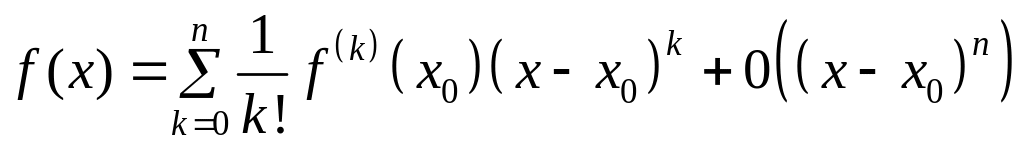(3')

называют формулой Тейлора для функции с остаточным членом в форме Пеано, а многочлен Тейлора (1) – многочленом наилучшего приближения.

Заметим, что формула ( ) является асимптотической (см. §6 гл. 4), поэтому, заменяя функцию на многочлен Тейлора в окрестности точки , мы не можем указать допущенную ошибку, а можем только указать порядок её малости. Отсюда ясна необходимость записать остаточный член в другой форме, в которой можно оценить его величину.

Будем искать остаточный член в виде , где – некоторая неизвестная постоянная. Предположим теперь, что функция имеет -ю непрерывную на отрезке производную и

-ю производную в каждой точке интервала . Перепишем формулу Тейлора ( ) в виде:

. (5)

Введём вспомогательную функцию:

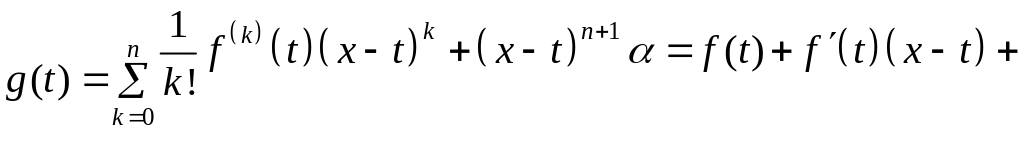
. (6)

Из (6) видно, что при , а при получим

то есть на концах отрезка функция принимает равные значения. Поскольку имеет непрерывную n-ую производную, то функция непрерывна на отрезке , а поскольку имеет -ю производную, то функция дифференцируема на интервале . Как видно удовлетворяет теореме Ролля.

Найдём производную функции .

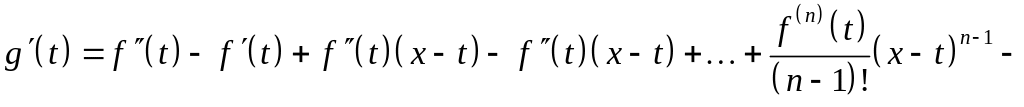
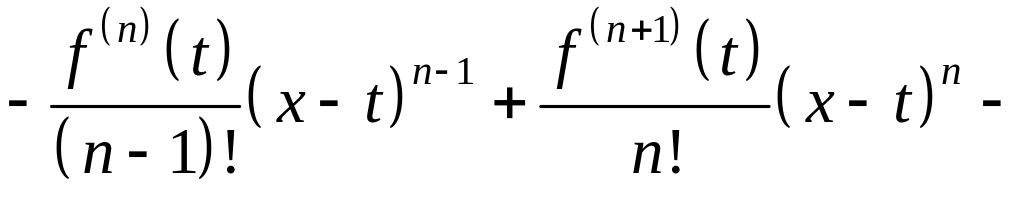
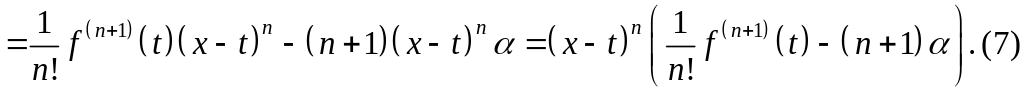Согласно теореме Ролля найдётся точка такая, что

Тогда из (7) найдём

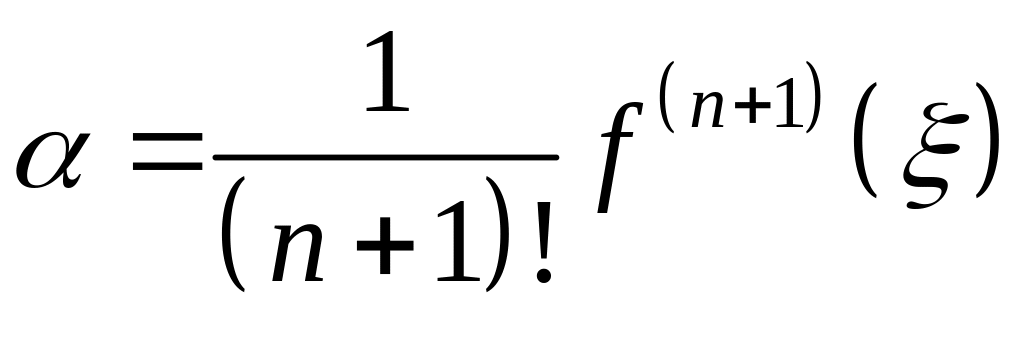. (8)

С учётом (8) формулу (5) перепишем так:

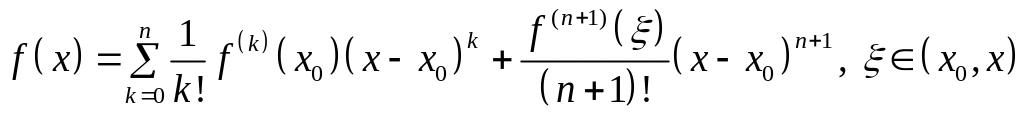. (9)

Формулу (9) называют формулой Тейлора с остаточным членом в форме Лагранжа.

Если ограничена в окрестности точки , то аппроксимируя функцию многочленом Тейлора, можно легко оценить возникающую при этом погрешность, если остаточный член формулы Тейлора записан в форме Лагранжа.

Заметим, что иногда точку в (4) удобнее записать в виде