§3. Некоторые следствия из теоремы Лагранжа. Теорема Дарбу
Теорема 1. Пусть функция дифференцируема на интервале . Тогда:
а) если
,
то функция монотонно убывает;
б) если
,
то
;
в) если
то функция монотонно возрастает.
Доказательство.
Пусть
,
– произвольные точки. Тогда на отрезке
функция
удовлетворяет
теореме Лагранжа.
. (*)
Если
то
и из (*) следует
,
то есть функция
убывает монотонно на
.
Утверждение а) теоремы 1 доказано.
Утверждения б) и в) доказываются аналогично.
Теорема 2 (Дарбу).
Пусть функция
дифференцируемая на
и пусть
.
Тогда найдётся точка
такая, что
,
то есть функция
подобно непрерывной функции принимает
все свои промежуточные значения между
и
.
Доказательство.
Пусть
(если
– доказательство аналогично). Положим
и введём две функции
и
,
если
. (1)
и
,
если
. (2)
Тогда
(3)
(см. рис.). Рассмотрим сложную функцию
.
(4)
Очевидно,
непрерывна на
как
суперпозиция, разность и отношение
непрерывных функций. Найдём предел
.
(Производная существует по условию теоремы).
Аналогично найдём
Доопределим функцию , положив
и 
Тогда функция будет непрерывной на отрезке и по теореме Коши (см. §11) принимает все свои промежуточные значения, то есть если
,
или ,
то найдётся точка
такая, что
.
(5)
Зафиксируем
и из (4) найдём:
(6)
Но на отрезке
функция
удовлетворяет
теореме Лагранжа (см. теорему 3 §2)
Сравнивая
(6) и(7) , получим
Что и требовалось доказать.
Следствие. Если
функция
дифференцируема на отрезке
,
то её производная
не имеет точек разрыва первого рода.
Доказательство.
От противного.
Пусть существует функция
дифференцируемая на
,
а её производная
строго возрастает на
и имеет в точке
разрыв первого рода (см. рис.). Пусть
и пусть
. (8)
Согласно теореме
2 производная
примет значение
,
причём
,
так как
строго возрастает. В силу строгой
монотонности
Получили противоречие (см. (8)). Это противоречие и доказывает следствие.
§4. Правило Лопиталя раскрытия неопределённостей
Теорема (Лопиталь).
Пусть функции
и
определены и дифференцируемы в некоторой
окрестности точки
,
за исключением быть может самой точки
.
Пусть
в окрестности точки
,
Тогда, если существует (конечный или бесконечный) предел
,
(1)
то существует
равный ему предел
то есть
. (2)
Доказательство. Если функции и не определены в точке , то доопределим их равенствами
Пусть
– произвольная
точка из окрестности точки
.
Тогда на отрезке
функции
и
удовлетворяют
теореме Коши.
.
(3)
Пусть
при
.
Тогда
при
Поскольку
предел (1) существует, то не зависит от
выбора последовательности, сходящейся
к точке
,
то есть
Перейдём к пределу в (3) при . Так как предел правой части (3) существует, то существует предел и левой части, то есть
Теорема доказана.
Формулу (2) называют
правилом Лопиталя раскрытия неопределённости
вида
Замечание 1. Если
и
удовлетворяют требованиям теоремы, то
правило Лопиталя можно применить
повторно.
Пример 1.
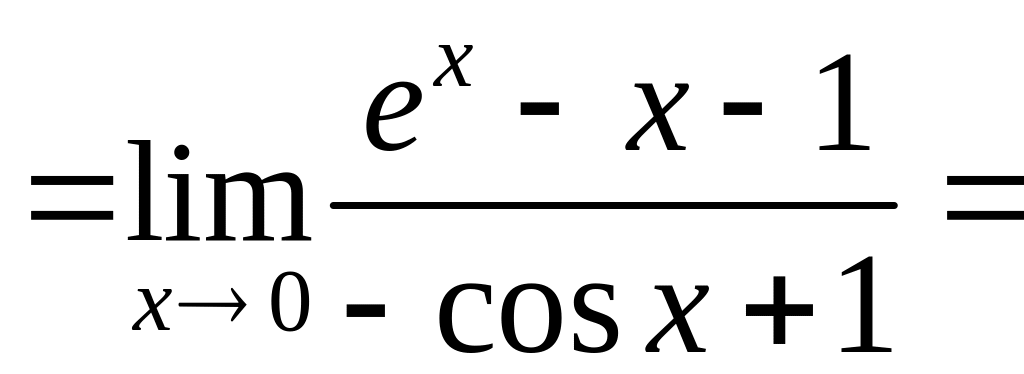
Здесь правило Лопиталя применено четыре раза.
Замечание 2. Можно
доказать, что правило Лопиталя применимо
и в том случае, когда точка
– бесконечно удалённая (
или
).
Пример 2.
Замечание 3.
Правило
Лопиталя можно применить и для раскрытия
неопределённостей вида
Пример 3.
при
Замечание 4. Если
не существует, то это не означает, что
не существует
Пример 4.
.
Применим правило
Лопиталя
.
Этот предел не существует.
Правило Лопиталя не применимо.
Замечание 5.
Правило
Лопиталя можно применить и для раскрытия
неопределённостей вида 0∙
,
,
если предварительно свести их к виду
или
Пример 5. Найти
предел
.
Решение.
Пусть
тогда
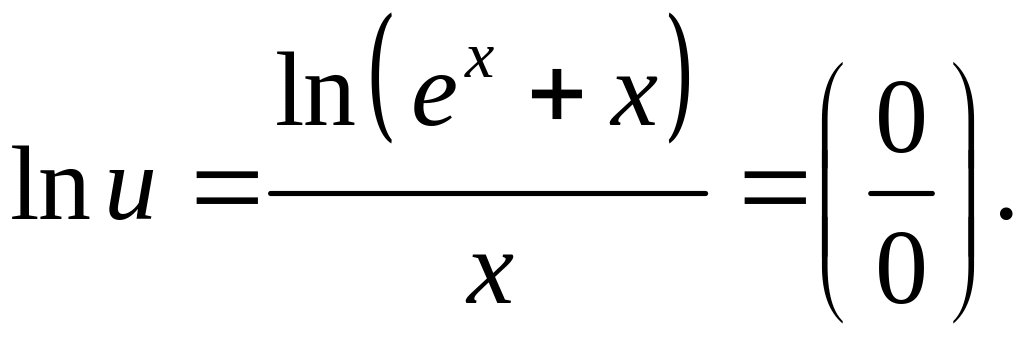
Применим правило Лопиталя.
Используя непрерывность логарифмической функции, найдём
