Найдём теперь второй дифференциал от сложной функции , . Дифференциал независимой переменной по-прежнему считается константой, но дифференциал промежуточной переменной является функцией независимой переменной и выносить его за знак дифференциала нельзя.

Используя инвариантность первого дифференциала, найдём

Итак,

. (4)

Поскольку то из (4) видно, что второй дифференциал не обладает свойством инвариантности формы. Не обладают этим свойством и все последующие дифференциалы.

Замечание. Разделим обе части (4) на , получим

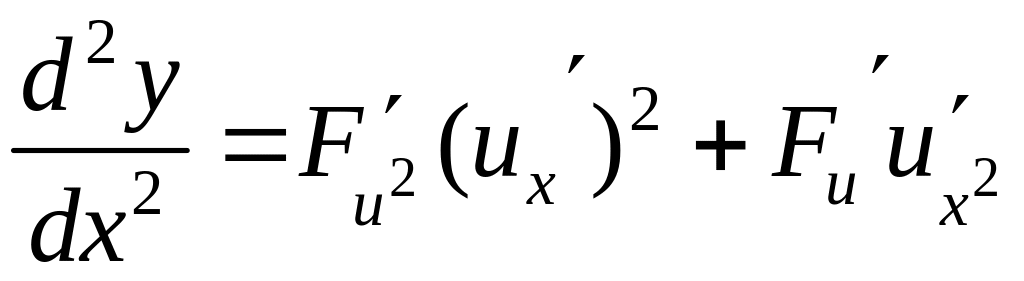. (5)

Формула (5) совпадает с формулой (1)§7, то есть

.

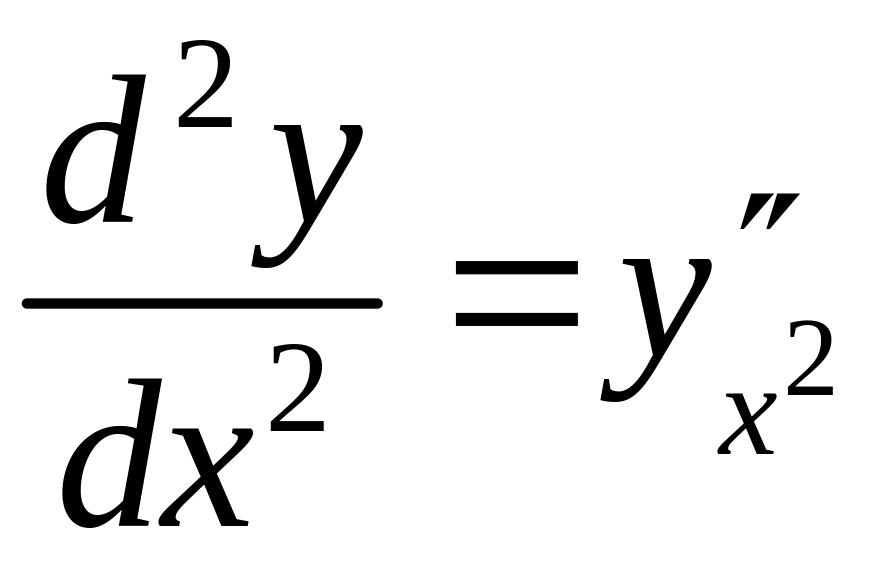Глава 6. Приложения дифференциального исчисления

§1. Возрастание функции в точке. Теорема Ферма

Пусть функция определена в некоторой окрестности точки . Говорят, что функция возрастает в точке , если существует некоторая окрестность точки , в которой функция возрастает, то есть

Аналогично определяется убывание функции в точке.

Теорема 1. Если функция имеет производную в точке и , то функция возрастает в точке .

Доказательство. .

Возьмём , тогда

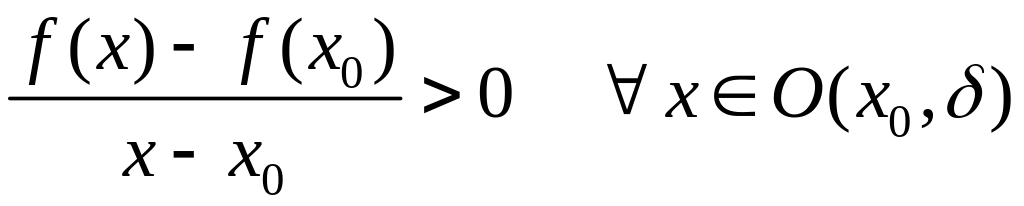. (1)

Неравенство (1) означает, что , если , и если , то есть функция возрастает в точке . Теорема доказана.

Очевидно, если то функция в точке убывает. Доказательство аналогично.

Замечание 1. Условие – достаточное, для возрастания (убывания) функции в точке . Но это условие не является необходимым. Например, функция возрастает в точке , но

Определение. Функция достигает в точке локального максимума, если существует такая, что

. (2)

m

0

Аналогично, если

, (3)

то в точке функция достигает локального минимума. Локальные максимум и минимум называются локальными экстремумами.

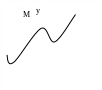
На рисунке – локальные минимумы, – локальный максимум.

Теорема 2 (Ферма). Если функция дифференцируема в точке и достигает в этой точке локального экстремума, то .

Доказательство. От противного. Если , то согласно теореме 1 функция в точке возастает, то есть не достигает локального экстремума. Если р , то убывает и также не достигает экстремума. Получили противоречие. Теорема доказана.

Геометрически теорема Ферма означает, что в точке ( , f ( )) график функции имеет горизонтальную касательную.

§2. Теоремы о среднем

Теорема 1 (Ролль). Если функция непрерывна на отрезке , дифференцируема на интервале а на концах отрезка принимает равные значения , то существует, по крайней мере, одна точка , в которой

Доказательство. Так как функция непрерывна на отрезке , то, согласно второй теореме Вейерштрасса (см. §10 гл. 4), она достигает на нём своего наименьшего и наибольшего значений.

Возможны два случая:

а) – const, следовательно, Теорема доказана.

б) . Так как , то, по крайней мере, одно из чисел или отлично от .

Допустим . Тогда , где . Это означает, что функция достигает в точке локального максимума. По теореме Ферма . Что и требовалось доказать.

Геометрически теорема Ролля означает, что между двумя точками, в которых значения функции равны, всегда найдётся точка, касательная в которой параллельна оси .

Следствие. Если функция непрерывна на , дифференцируема на , но , то . Доказательство от противного.

Теорема 2 (Коши). Если функции и непрерывны на , дифференцируемы на , причем , то существует точка такая, что

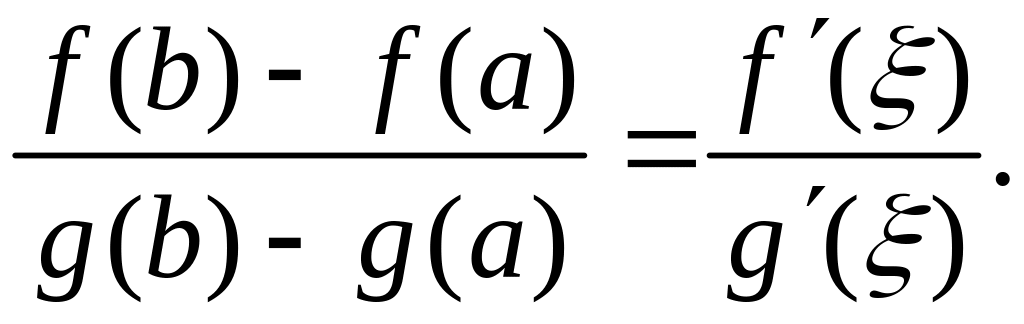(1)

Доказательство. Составим вспомогательную функцию , где – некоторый коэффициент. Подберём его так, чтобы функция удовлетворяла условиям теоремы Ролля, то есть потребуем равенства на концах отрезка , так как все другие требования теоремы Ролля выполняются).

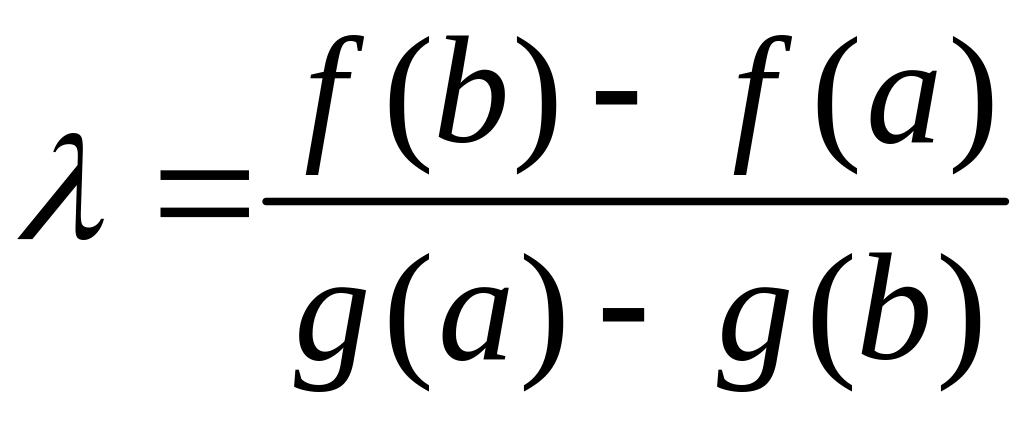. (2)

согласно следствию теоремы Ролля).

Итак, если коэффициент определяется формулой (2), то функция удовлетворяет теореме Ролля, то есть

Или

.

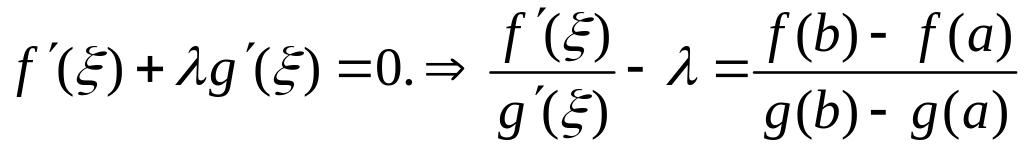Теорема доказана.

Теорема 3 (Лагранж). Если функция непрерывна на отрезке и дифференцируема на интервале , то существует точка такая, что

. (3)

Доказательство. Положив в теореме Коши , получим

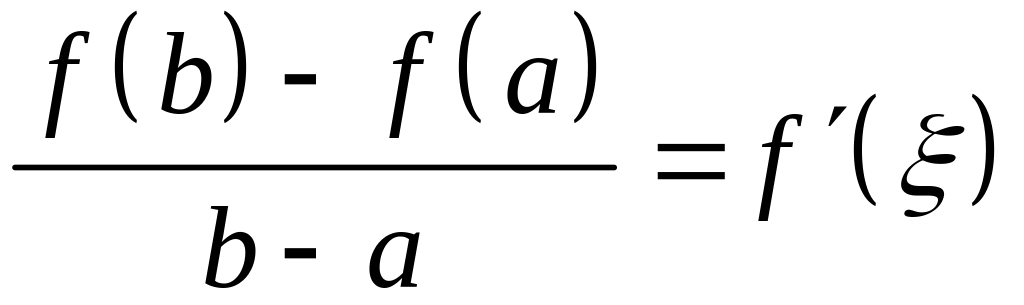или

Теорема доказана.

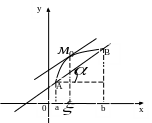
Из рис. видно, что 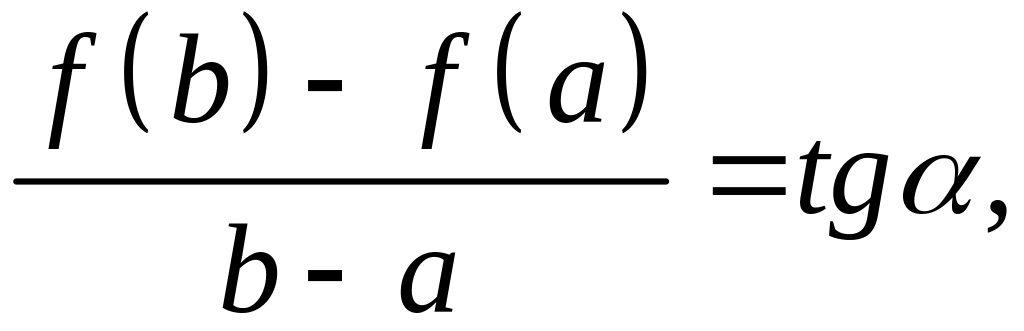где – угол наклона секущей , а из (3) видно, что , то есть теорема Лагранжа утверждает, что между точками и кривой существует точка такая, что касательная в этой точке параллельна секущей.

Замечание. Пусть удовлетворяет теореме Лагранжа и пусть Тогда согласно (3)

или . ( )

Или где Равенства ( ) и (3) называют формулой конечных приращений. Формула ( ) – это точное равенство для любых конечных (в отличие от приближённого ).

Во всех трёх теоремах речь идёт о существовании некоторой средней точки , поэтому эти теоремы и называют теоремами о среднем.