3) Операторный способ

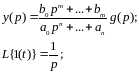
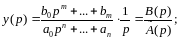
Далее по таблице можно найти обратный переход: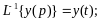

Если найти корни 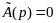pi=0,p_1…

Воспользуемся формулой разложения:

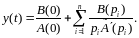
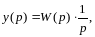
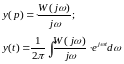- обр-е пр-е Фурье.

12. Критерии кач-ва рег-ния.

Показатели кач-ва сис-мы б. прямые и косвенные

П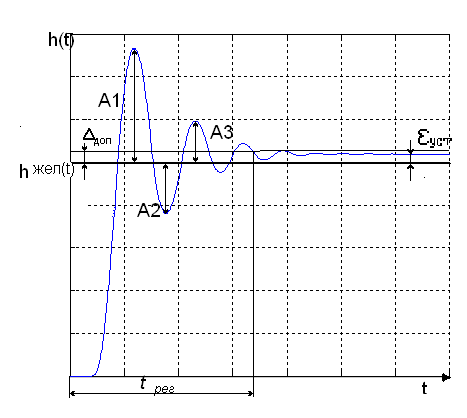 рямые опред-ся на основе графика перех-й хар-ки.

ε_уст – устан-шаяся ошибка.

∆_доп–доверит-й интервал ошиб-ки: если доп-й интервал не задан, то по умолчанию мы принимаем его 5% от h_жел.

Быстрод-е - время, в течение кот-го перех-я х-ка войдёт в доверительный интервал и уже не выйдет, это время и есть время регулирования t_рег.

Перерег-ние – макс-е знач-е вых-го пар-ра, амплитуда hmax. Если перейти к безразм-м единицам, то перерег-ние будет хар-ся:

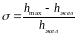*100%

Степень затухания - данный показатель получаем, сопоставляя амплитуды переходной характеристики следующим образом:

.

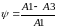Колебат-сть сис-мы хар-ся числом колебаний регулируемой в-ны за время ПП-са tрег(tп). Если за это вр. ПП в сис-ме совершает число колеб-й меньше зад-го по усл-м технологии, тот считается, что с-ма им-т треб-е кач-во регул-я в части ее колебательности.

Устан-ся ошибка εуст опред-ся как раз-сть м/ду устан-мся знач-м рег-мой в-ны после окончания ПП и ее зад-м знач-м:

εуст=hжел-hуст.

Косвенные критерии качества регулирования

1) ПП-с сущ-но зав-т от корней ХАУ. Для оценки качества рег-ния исп-ся понятие “средний геометрический корень”- Ω.

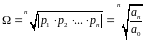, где p_1..p_n – корни ХАУ, а 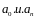- соответствующие коэффициенты ДУ.

Из ур-я следует, что для повышения быстродей-я сис-мы следует ув-ть коэф-т a_{n .} Чем больше величина Ω , тем у системы большее быстрод-е. Если допустить что корни веществ-е и отриц-ны, то корень, кот. в координатах Im(Re) будет ближе к мнимой оси, будет затягивать ПП.

Если ближайший корень к мнимой оси будет следующим:

,

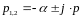тогда ПП будет затягиваться этой парой корней и решение будет зависеть от p_1,2. Перейдём к след. виду

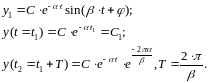
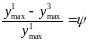
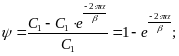ψ – степень затухания.

Оценка кач-ва по показателю колебательности(зн-е ординаты Mmax амплитудной хар-ки

зам-й сис-мы при нач-ой ординате равной 1)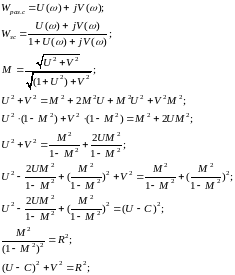

В результате получили уравнение окружности с радиусом R и с центром в точке (C,0): R=M/1-M²; C=M²/1-M²

13. Синтез системы рег-ния м-дом расчета пар-в рег-ра на желаемую степень затух-я пп.

Пусть ориент-но выбран рег-р. При оценке качества систем упр-ния на основе косв-х м-дов была получена зав-сть степени ψ затухания от ближайшего к мнимой оси корня, связанного с параметром m: 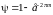(2.7). При m = 0 имеем границу области устойчивости. Чаще всего выбирают значение m от 0,22 (ψ = 0,75) до 0,366 (ψ = 0,9). Пусть в комплексной плоскости корней ХАУ мнимая ось сдвинута до совпадения с корнем, местополож-е кот-го х-ся пар-ром m. Такому смещению мнимой оси соотв-т подстановка частотной области p = mω ± jω. (2.8)

Исходя из условия «попадания» одного из корней на мнимую ось можно в соответствии с критерием Найквиста записать

W_p(mω ± jω)∙W_oб(mω ± jω) = 1. (2.9)

Из уравнения (2.9) можно получить два уравнения:

A_pA_oб = 1; (2.10), φ_p + φ_oб = 0,(2.11)

где A_p, A_oб  соотв-но АЧХ и φ_p, φ_oб  ФЧХ рег-ра и объекта.

Рассмотрим особенности расчета параметров регуляторов.

При расчета П-регулятора k_пр равен A_p. Нулевой сдвиг фазы пропорционального регулятора заменим на –π. Тогда уравнения (2.10), (2.11) примут вид: k_пр∙ A_oб(mω ± jω) = 1; (2.12), π + φ_oб(mω ± jω) = 0. (2.13)

Из уравнения (2.13) найдем частоты, а затем на основании уравнения (2.12) определим k_пр.

При расчете ПИ-регулятора искомыми коэф-ми будут k_пр и коэффициент при интегральной составляющей k_и. Перепишем уравнение (2.10), (2.11) с учетом искомых коэффициентов k_пр и k_и:

A_p(m, ω, k_пр, k_и)∙A_oб(m, ω) = 1; (2.12)

φ_p(m, ω, k_пр, k_и) + φ_oб(m, ω) = 0. (2.13)

Для произвольно заданных значений ω < ω_гр можно найти мн-во знач-й k_пр и k_и, кот-е будут обеспеч-ть желаемую степень затухания ПП. Граничную частоту ω_гр можно опр-ть из условия:

A_oб(ω_гр) ≈ 0. (14)

Имея массив коэф-тов, можно ввести дополнительные критерии качества регулирования для нахождения лучшей пары k_{пр и} k_и.

При расчете ПИД-регулятора тесно свяжем коэффициент при дифференцирующей составляющей k_Д с коэффициентом k_и:

k_и  k_D ≈ (0,1÷0,15).

Весь дальнейший расчет ПИД-регулятора аналогичен расчету для ранее рассмотренного ПИ-регулятора.