30. Адаптив-е системы упр-я. Классифик-я. Синтез адапт-й системы с эталонной моделью на основе подстройки коэф-в ур-ния переем-х состояний.

Рассм-м ОУ, возмущенное дв-е которого опис-ся уравнениями:

;

,

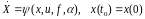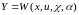где x(t)  nмерный вектор переменных состояния объекта, y(t) rмерный вектор измеряемых (выходных) переменных, f(t), (t)  s и мерные векторы внешних возмущений и помех соответственно, (t)  lмерный вектор неизвестных параметров объекта, u mмерный вектор управления.

Пусть в первом приближении можно воспользоваться линейной нестационарной моделью вида

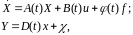
где часть или все элементы матриц A(t), B(t), (t), D(t) являются неопр-ми параметрами, из которых можно составить вектор

.

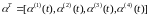Системы с адаптивной оценкой параметров

Предн-ны для восстан-я неизвестной х-ки объекта, описываемой конечно-мерным вектором Q веществ-х пар-в, на основе оценки сигналов системы в реальном масштабе времени. Оценка конечномерных пар-в модели по инф-и о сост-и моделируемой системы м.б. описана регресс-м вектором сигнала (t). Адапт-я оценка состоит в том, что на основе регресс-го вектора сигнала (t), оценки пар-тра за прошлое время 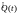и сигнала ошибки e(t) коррект-ся или заново вычисл-ся оценка пар-ра. Сигнал ошибки e(t) вычисляется как разность между сигналом, восстан-ным с с пом-ю , и опорным знач-м критерия качества, заданным или вычисляемым по измерениям параметров объекта.

Если сов-сть внешних сигналов, действ-х на систему, обозн-ть w(t), то полная адаптивная система может быть представлена в виде трех взаимосвязанных подсистем.

Подсистемы регрессии, на вход которой поступают сигналы w(t) и , а на входе формируется сигнал (t) в виде

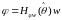. (7.1)

Подсистема обычно вкл-т как ОУ, так и рег-р с замкнутой ОС.

Подсистема ошибки, на вход которой поступают сигналы w(t), (t) и , а на выходе образуется сигнал ошибки e(t) для адаптивной коррекции в виде 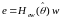. (7.2)

П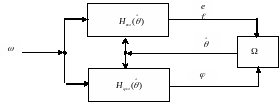 одсистема адаптации, в которой е и  используются для получения оценок параметра 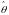в виде

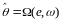. (7.3)

Объединяя перечисленные подсистемы в одну структурную схему, получим систему, приведенную на рис.7.1.

Рис. 7.1 Адаптивная система

Модель адаптивной системы рис. 7.1 имеет вид

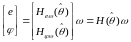, (7.4) где .

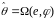Адаптивное упр-ние с эталонной моделью в перем-х сост-я

Пусть имеем полностью управляемый и полностью наблюдаемый объект управления вида:

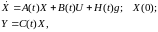(7.87)

где А, В, Н, С – неизвестные матрицы чисел известных размеров nn, nm, rn соответственно; g–m–мерный вектор задающих воздействий.

Необходимо найти регулятор, обеспечивающий близость вектора измеряемых переменных объекта относительно желаемого вектора, который задается эталонной моделью вида:

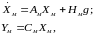(7.88)

где Ам, Нм, См – известные матрицы чисел, Хм – вектор состояний модели, Yм – вектор выходов модели.

Цель адаптации 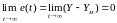. (7.89)

Вначале рассмотрим решение данной задачи для случая yi = xi, 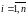, а размерность вектора управления равна размерности вектора переменных состояния при единичной матрице В.

Адаптив-ый р-тор, обеспечив-й настройку коэф-тов уравнения состояния

В соотв-и с прин-ми упрощ-ми перепишем ур-ние (7.87) в виде

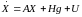,(7.90) а уравнение модели 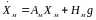. (7.91)

Выберем элементы матрицы Ам такими, чтобы матрица Ам была гурвицевой, а структура регулятора в виде 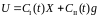, (7.92)

где CI(t), CII(t) – матрицы настраиваемых пар-ров регулятора.

Поскольку размерности матриц А, СI и Н, СII совпадают, то регулятор изменяет каждый из коэффициентов уравнения состояния и поэтому искомый алгоритм носит название алгоритма настройки коэффициентов уравнения состояния.

Замыкая ур-ние (7.90), ур-нием (7.92) и вычитая из него (7.91)

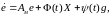(7.93) где 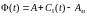(7.94) 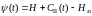.(7.95)

Составим функцию Ляпунова

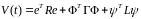,(7.96) где R, Г, L – положительно определенные матрицы.

Пусть полная производная функции 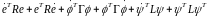(7.97)

= из усл-й уст-ст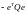и , где Q – полож-но опр-ная матрица. Тогда имеем следующую систему матричных уравнений:

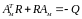(7.98) 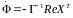(7.99) 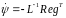. (7.100)

Используя зависимости (7.94, 7.95) и считая что на интервале адаптации А, Ам, Н и Нм остаются постоянными, перепишем выражения (7.99, 7.100) в виде:

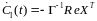; (7.101) 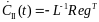.(7.102)

В результате имеем адаптивный регулятор:

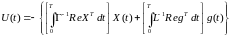. (7.103)