2.3 Метод дихотомії .

Методи мінімізації унімодальних функцій застосовують на кожному з отриманих інтервалів унімодальності і служать для відшукання точок локального мінімуму із заданою точністю . Розглянемо два методи мінімізації, які не вимагають диференціювання функції мети .

Метод дихотомії дозволяє на кожному кроці зменшити у двічі довжину інтервалу, що містить точку мінімуму.

Хай відрізок є відрізком унімодальності функції . Розділимо його на чотири рівні частини точками:

, , , , , де . Обчислимо , , ... . значення функції в цих точках.

Серед точок вибираємо точку , значення функції в якій якнайменше. Далі вибираємо новий інтервал. Якщо – внутрішня точка інтервалу , то новий інтервал з центром в точці і завдовжки . У разі коли новий інтервал . Якщо ж , тоді інтервал .

Отриманий відрізок використовується як початковий і процедура повторюється знов до тих пір, доки довжина отриманого відрізка не стане менше , де - задана точність. Як наближена точка локального мінімуму вибирається середина останнього інтервалу. Мінімальним значенням вважається значення функції в точці.

Глобальна збіжність методу для унімодальних функцій виходить з визначення. Швидкість збіжності лінійна з коефіцієнтом щодо довжини відрізка.

Приклад 2.2

З точністю знайти точку локального мінімуму функції на відрізку унімодальності

;

Розділимо початковий відрізок на чотири частини точками , , , , .

Обчислимо значення даної функції в цих точках і занесемо їх в таблицю 2.3:

Таблиця 2.3

	0	1	2	3	4
	8.6	8.75	8.9	9.05	9.2
	-5.5968	-5.7784	-5.8302	-5.7511	-5.5429

Значення є найменшим, на наступному кроці розглядаємо відрізок . Його довжина рівна більше . Тому процедуру повторюємо. Обчислимо

Розділимо відрізок на чотири частини точками .

Значення і занесемо в таблицю 2.4:

Таблиця 2.4

	0	1	2	3	4
	8.6	8.75	8.9	9.05	9.2
	-5.778	-5.8207	-5.8302	-5.807	-5.7511

є найменшим значенням, тому новий відрізок . Оскільки його довжина менше , то як точка мінімуму вибираємо , мінімальне значення

2.4 Метод «золотого перетину».

Метод отримав свою назву через те, що на кожному кроці відрізок ділиться на дві нерівні частини і так, щоб відношення довжини всього відрізка до довжини більшої частини дорівнювало відношенню довжини більшої частини відрізка до довжини меншої

Такий розподіл називається «золотим перетином», число – «золотим відношенням». З вказаних пропорцій легко отримати координати точки :

Точка розташована на відрізку симетрично до і тому

Обчислимо значення функції в точках і виберемо новий відрізок таким чином:

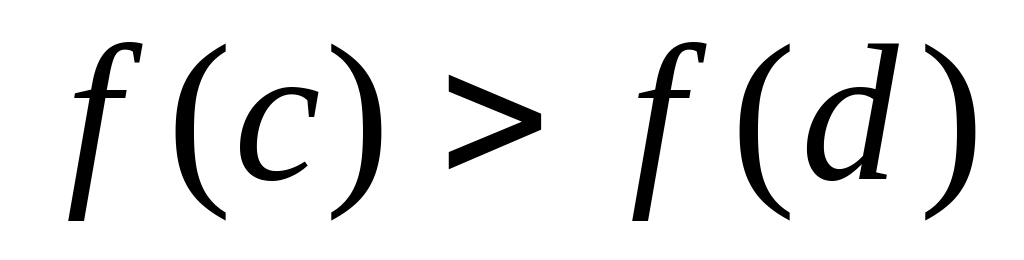1. Якщо , то вважаємо .

Тоді стає лівою точкою “золотого перетину” відрізка . Для правої точки маємо:

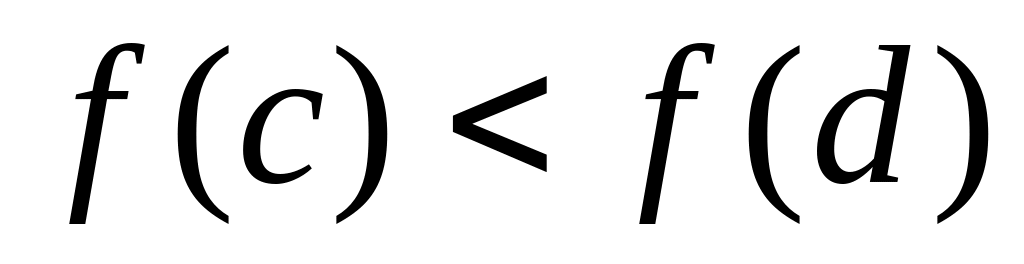2. Якщо , то вважаємо 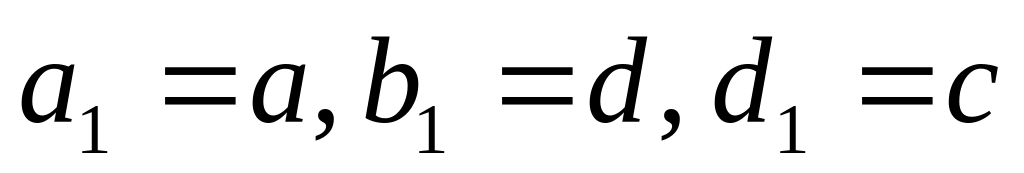. Точка стає правою точкою “золотого перетину” відрізка. Для лівої точки маємо: .

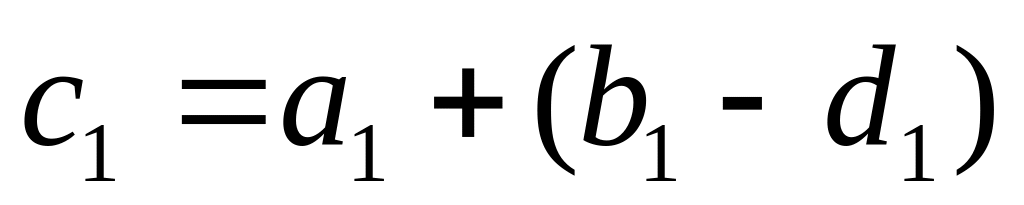Мал. 2.2. Вибір нового відрізка методом «золотого перетину»

3. У разі, коли порівнюємо і .Якщо , то відрізок вибирається як в першому випадку: , , , . Якщо ж , то відрізок вибирається як в другому випадку , , , . Процес розподілу відрізків продовжується до тих пір, доки довжина отриманого відрізка не стане менше . Як точка локального мінімуму вибирається точка .

Швидкість збіжності цього методу лінійна з коефіцієнтом 0,618.

Приклад 2.3. Знайти точку локального мінімуму функції на відрізку унімодальності з точністю методом золотого перетину.

Відрізок ділимо на три частини точками

1. Обчислимо значення функції в точках і

;

Оскільки , тоді ,

.Оскільки , тоді процес дроблення продовжується

2. .

Обчислимо . Оскільки , тоді ; ; ; ; .

3. .

Обчислимо . Оскільки , тоді

; ; ; ;

4. .

Обчислимо . Оскільки , тоді

; ; ; ; .

5. .

Обчислимо . Оскільки , тоді

; ; ; ; .Обчислимо .

6. Довжина відрізка рівна , вона менше , тому дроблення відрізків завершено.

Точка локального мінімуму .

Значення функції в цій точці .

Обчислення занесемо в таблицю 2.5.

Таблиця 2.5

0	2.3	2.5293	-5.8159	2.6707	-5.8169	2.9
1	2.5293	2.6707	-58169	2.7585	-5.7588	2.9
2	2.5293	2.6172	-5.8302	2.6707	-5.7169	2.7586
3	2.593	2.5828	-5.8300	2.6172	-5.8302	2.6707
4	2.5828	2.6172	-5.8302	2.6363	-5.8274	2.6707
5	2.5828	2.6019	-5.8310	2.6172	-5.8302	2.6363
6	=2.60955			=-5.83075

Питання для самоперевірки

1. Що називається точкою локального мінімуму функції ?

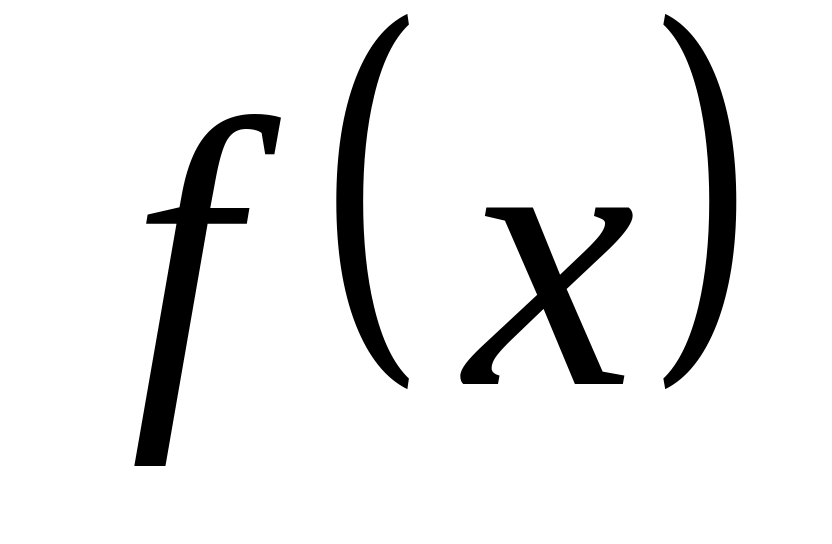2. Які етапи пошуку мінімуму?

3. Який алгоритм методу відділення відрізків унімодальності?

4. Як визначається точка мінімуму методом дихотомії?

5. Яке співвідношення визначає «золотий перетин»?

6. Який алгоритм методу ” золотого перетину”?

Література, що використовується

1. [4] стор. 4-19

3. ЛЕКЦІЯ 3. ГРАДІЄНТНІ МЕТОДИ МІНІМІЗАЦІЇ

ФУНКЦІЇ ДЕКІЛЬКОХ ЗМІННИХ.

План лекції

1. Постановка задачі.

2. Метод найшвидшого градієнтного спуска.

3. Метод градієнтного спуска з дробленням кроку.

4. Метод градієнтного спуска з постійним кроком.

5. Метод по координатного спуска.

3.1 Постановка задачі.

Задача багатомірної мінімізації без обмежень полягає в перебуванні точці з , у який функція мети , має мінімальне значення. Будемо припускати, що визначено і має безупинні частки похідні для усіх .

Виз. Точка називається точкою локального мінімуму функції , якщо знайдеться - окіл точки такий, що для усіх з цього околу має місце .

Точка належить - околу точки , якщо відстань від до менше , тобто

Виз. Функція, що має єдиний локальний мінімум у деякій області , називається унімодальною на цій області.

Виз. Градієнтом функції F(x) називається вектор

Величина градієнта

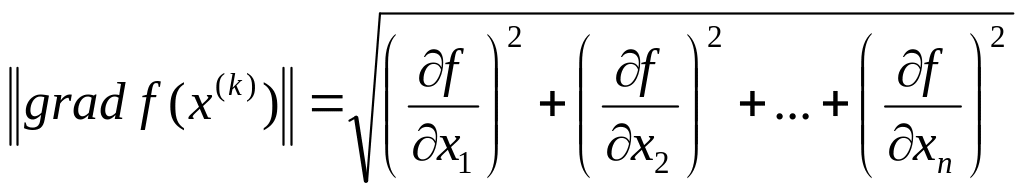
показує найбільшу швидкість зміни функції у точці , а напрямок його збігається з напрямком найбільшого зростання функції. Вектор називається антиградієнтом і вказує напрямок найбільшого убування функції.

Точка локального мінімуму міститься в безлічі рішень системи нелінійних рівнянь , .

Однак, не всі рішення системи є точками екстремум функції. Для того, щоб точка була точкою локального мінімуму функції , досить перевірити виконання наступних умов:

1. :

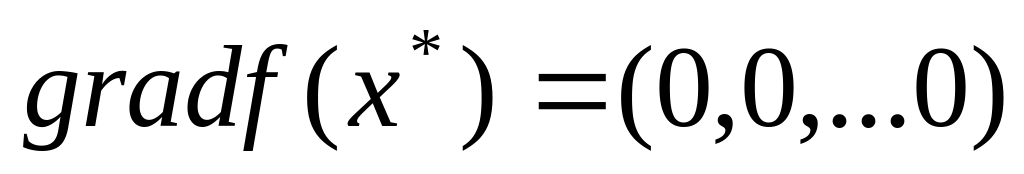2. матриця Гесса в точці 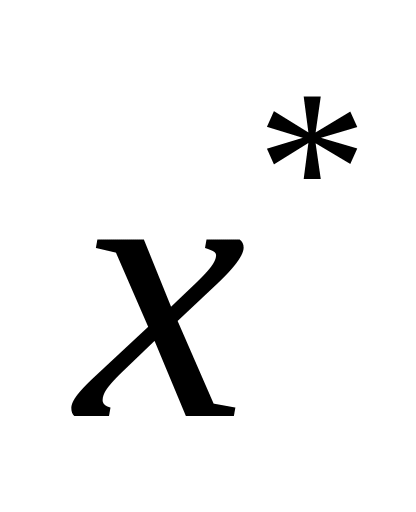позитивно визначена.

Матрицею Гесса називається матриця розмірами , елементами якої є частинні похідні другого порядку функції

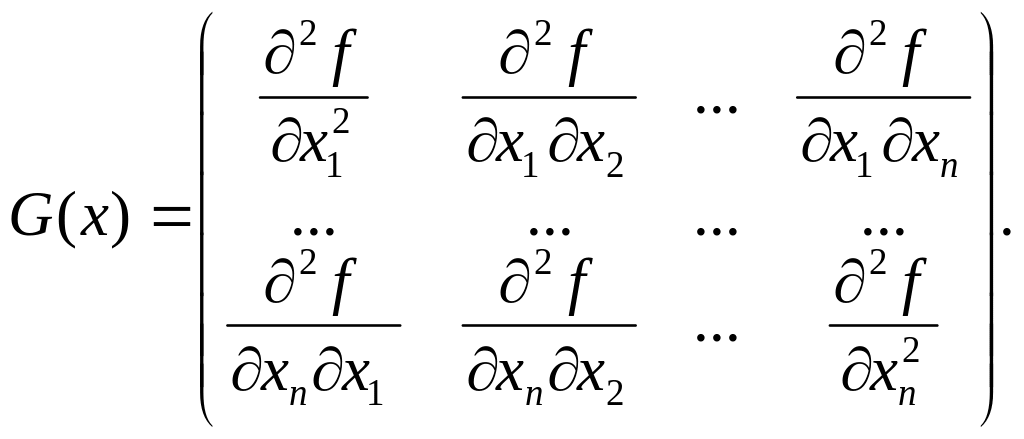
Матриця 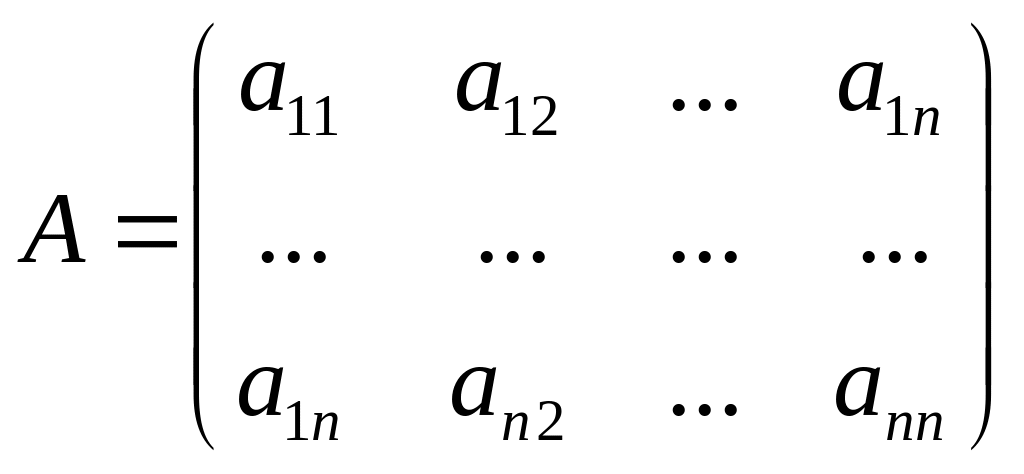називається позитивно визначеною, якщо всі її власні значення позитивні.

Власні значення матриці А визначаються як рішення рівняння

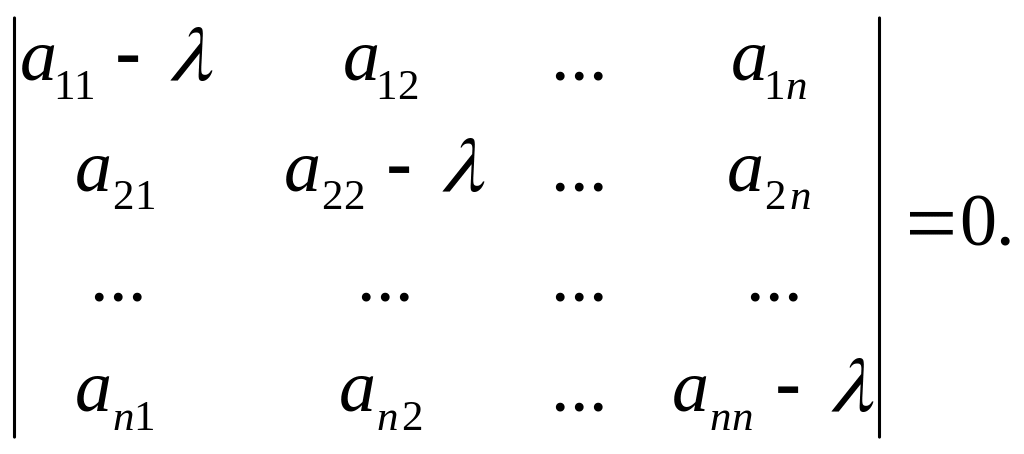
Рівняння має рішень називають власними числами матриці .

Пошук точок локального мінімуму можна виконати в два етапи:

1. Рішення системи лінійних рівнянь;

2. Вибір серед знайдених рішень точок локального мінімуму.

Кожний з етапів пошуку досить складний, тому на практиці найбільше часто використовуються прості ітераційні методи пошуку точок локального мінімуму. Ітераційні методи чи мінімізації методи спуска складаються в побудові послідовності

,

що сходиться до точки локального мінімуму . Тут – вектор, який вказує напрямок спуска, а – число, що змінює довжину кроку спуска в зазначеному напрямку. Розглянемо градієнтні методи спуска. Градієнтними називають методи спуска, у яких визначається напрямком антиградієнта в точці: або

1. Різні градієнтні методи відрізняються лише способом вибору кроку. Тому виділимо два класи методів: методи в яких величини задані заздалегідь і не залежать від точок спуска ;

2. Методи, у яких величини обчислюються для кожної точки .

Прикладом методів першого класу є метод розбіжного ряду. У ньому послідовність вибирається так, щоб виконувалися умови:

1. при ;

2. (наприклад, ). Однак швидкість збіжності методу мала. До того ж класу відносяться методи градієнтного спуска з постійним кроком і з дробленням кроку, розглянуті нижче.

Найбільш відомим методом другого класу є метод найшвидшого спуска.