1.4 Метод Симпсона.
Хай
вимагається приблизно обчислити
розіб'ємо інтервал
на
рівних
частин точками
. Хай відомі значення функції у вузлах
розбиття:
Мал. 1.3. Геометрична інтерпретація методу Симпсона.
Як
елементарне виберемо інтервал
.
По трьох відомих значеннях функції
будуємо многочлен Лагранжа другого
порядку, використовуючи коефіцієнти
Котеса; отримаємо наближену формулу:
Погрішність формули Симпсона на визначається:
Геометрично
це означає заміну на [
]
дуги кривій
дугою параболи, що проходить через три
точки
.
Значення визначеного інтеграла на визначається:
.
Метод Симпсона мають п'ятий порядок точності відносно h для локальної погрішності і четвертий для глобальної.
1.5 Правило Рунге для обчислення наближеного значення погрішності.
Хай
невідоме точне значення деякої величини;
невідоме точне значення, обчислюване
з кроком h,
хай встановлено співвідношення:
(1.1)
де
- нескінченно
мала
відносно
;
,
не залежна від
;
- відомі
цілі значення.
Позначимо
через
наближене значення, знайдене з половинним
кроком.
(1.2)
З формули (1.1) віднімемо формулу (1.2):
Виразимо
Знайдене значення підставимо у формулу (1.2), отримаємо:
Тоді наближена оцінка погрішності може бути визначений таким чином:
.
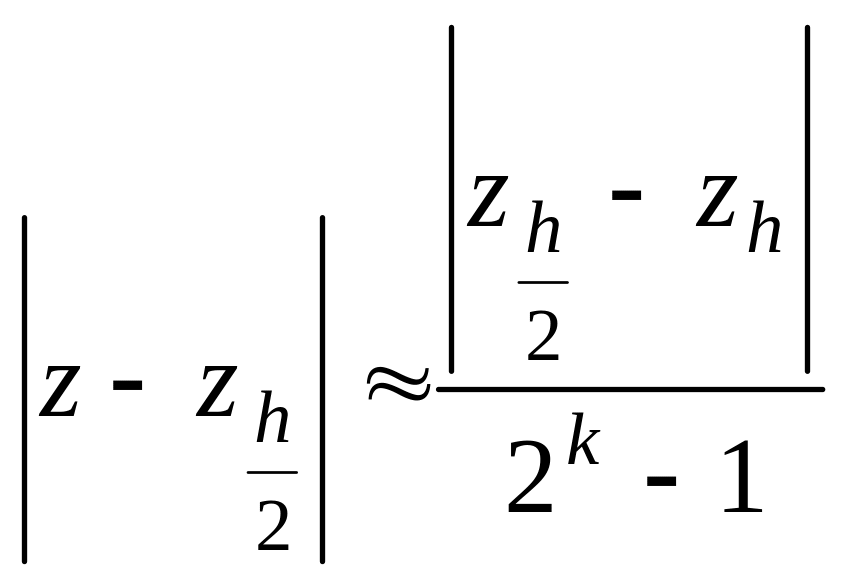1.6 Уточнене по Річардсону наближене значення.
Помножуємо
формулу (1.2)
на
;
з неї віднімаємо формулу (1.1):
Виразимо точне значення:
Уточнене по Річардсону наближене значення визначається формулою:
Для точного значення z запишемо:
Уточнене
по Річардсону значення має порядок
точності
,
в той час, як
і
мають порядок точності
відносно
.
Застосування правила Рунге для оцінки наближеного значення визначеного інтеграла.
Хай
точне значення визначеного інтеграла;
- наближені значення з кроками
. Хай відоме співвідношення:
де
для
формули прямокутника і трапеції;
для
формули Симпсона.
Тоді погрішність наближеного значення визначеного інтеграла за правилом Рунге обчислюється:
Уточнене по Річардсону наближене значення рівно:
Обидві
формули мають порядок точності
відносно
.
Приклад 1. 1
Знайти наближене значення визначеного інтеграла методом трапеції і Симпсона.
Розіб'ємо інтервал інтеграції на 4 частини з кроком =0.25. Значення функції у вузлах розбиття занесемо в таблицю:
-
0
0.25
0.5
0.75
1
0
0.0624
0.247
0.533
0.841
Обчислимо наближені значення з кроком :
а) Метод трапеції:
б) Метод Симпсона:
Розіб'ємо [0,1] на 8 частин з кроком
|
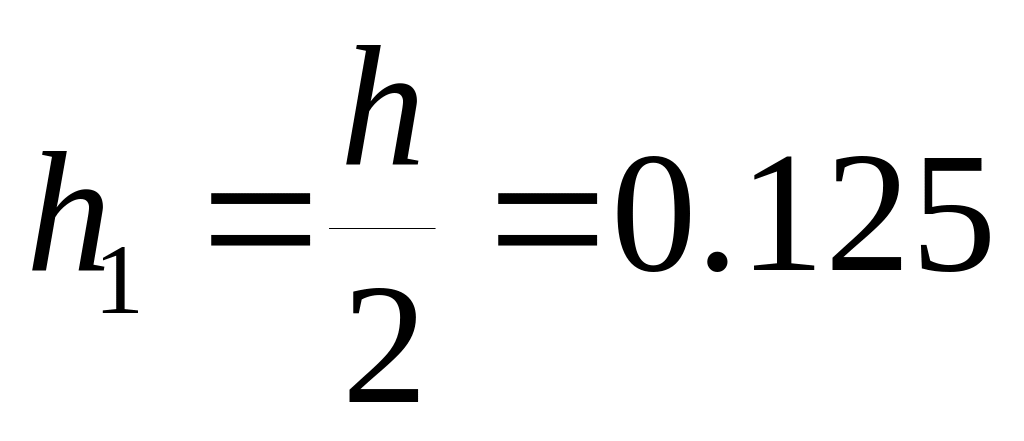
0 |
0,125 |
0,25 |
0,375 |
0,5 |
0,625 |
0,75 |
0,875 |
1 |
|
0 |
0,0156 |
0,0624 |
0,1402 |
0,247 |
0,3808 |
0,533 |
0,693 |
0,841 |
Обчислимо наближені значення з половинним кроком:
.
Оцінимо погрішність наближених значень визначеного інтеграла, обчисленого з половинним кроком:
Обчислимо уточнені по Річардсону наближені значення:
