Питання для самоперевірки

1. Які параметри розподілу, застосовувані в математичній статистиці ?

2. Яким чином визначаються точені й інтервальні оцінки цих параметрів ?

3. Які найбільш важливі розподіли, застосовувані в математичній статистиці ?

4. Як визначаються полігон і діаграма частот ?

Література, що використовується

1. [12] стор.8-13

2. [6] стор.6-10

6. ЛЕКЦІЯ 6. СТАТИСТИЧНА ПЕРЕВІРКА ГІПОТЕЗ

План лекції

1. Статистична гіпотеза. Статистичний критерій. Помилки, що виникають при перевірці гіпотез.

2. Перевірка гіпотези про нормальний розподіл помилок експерименту.

3. Перевірка гіпотези про погодженість думок експертів (апріорне ранжирування змінних).

6.1 Статистична гіпотеза. Статистичний критерій. Помилки, що виникають при перевірці гіпотез.

Виз: Статистичної називають гіпотезу про вид невідомого розподілу або про параметри відомого розподілу.

Наприклад, гіпотеза - випадкова величина розподілена за нормальним законом.

Виз: Нульовий (основний) називається висунута гіпотеза .

Виз: Альтернативної (конкуруючої) називається гіпотеза, що суперечить основний.

Конкуруючих гіпотез може бути кілька.

Наприклад, основна гіпотеза - математичне очікування випадкової величини Y дорівнює 5 :

конкуруючі: :

:

:

Виз: Статистичним критерієм ( ) називається випадкова величина, точний або наближений розподіл, який відомо і яка служить для перевірки справедливості нульової гіпотези.

Множина можливих значень критерію ділиться на дві непересічні області:

1. значення, при яких нульова гіпотеза справедлива (область прийняття гіпотези).

2. значення, при яких нульова гіпотеза відкидається (критична область).

Критична область може бути однобічної (лівосторонньої, правобічної) або двосторонньої.

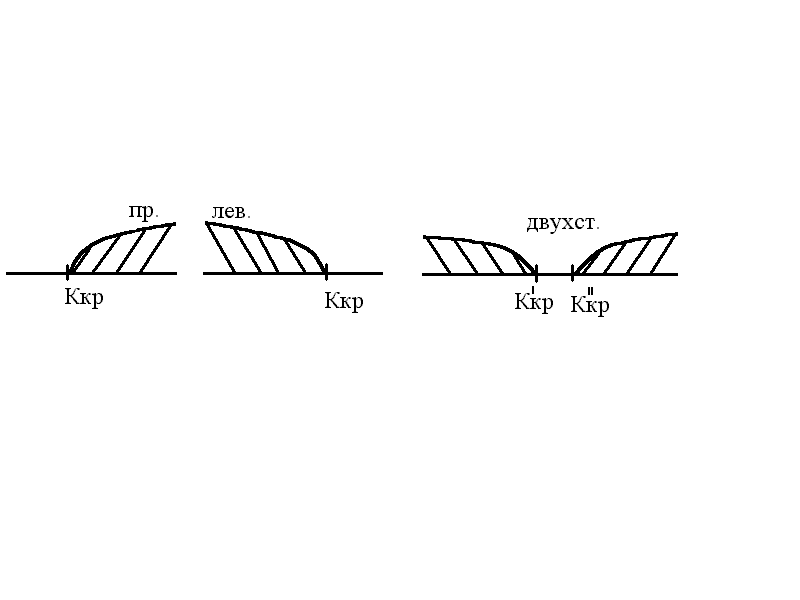Мал.2. Види критичних областей: правобічна, лівостороння й

двостороння.

Точка , що відокремлює критичну область від області прийняття гіпотези, називається критичною точкою.

Щоб визначити критичну область, вибирають число - рівень значимості. - імовірність того, що при справедливості нульової гіпотези значення критерію попадає в критичну область. Тоді для правобічної критичної області визначається з умови:

.

Значення критерію є табулірованім, тобто можна знайти по таблиці розподілу критичних точок залежно від рівня значимості і числа ступенів волі . Спостережуване значення критерію визначається за результатами експерименту.

Якщо < , то гіпотеза H₀ приймається. Якщо > , то відкидається, а приймається конкуруюча гіпотеза H₁.

Для лівосторонньої критичної області критична крапка визначається з умови:

.

Для двосторонньої:

Якщо двостороння область симетрична відносно початку координат, то:

Тому що спостережуване значення критерію визначалося за результатами експерименту, те - випадкова величина й, отже, можуть виникати помилки при прийнятті гіпотези. Розрізняють помилки першого й другого роду. До помилок першого роду відносять ті, при яких відкидається правильна гіпотеза. До помилок другого роду, відносять ті, при яких приймається неправильна гіпотеза. Припустимою ймовірністю помилки першого роду є - рівень значимості. Однак. якщо зменшувати , то зростає ймовірність прийняття невірної гіпотези, тобто ймовірність помилок другого роду. Якщо справедливо гіпотезу , то це вважається доведеним, якщо справедливо гіпотезу - те говорять, що результати експерименту не суперечать нульової гіпотези. Для того щоб уважати доведеної потрібно або знову повторити експеримент або перевірити гіпотезу за допомогою інших критеріїв.

ПОРЯДОК ПЕРЕВІРКИ СТАТИСТИЧНИХ ГІПОТЕЗ.

1. Вибір нульової й альтернативної гіпотез і .

2. Вибір критерію і рівня значимості .

3. Обчислення за результатами експерименту.

4. Пошук по таблиці розподілу критичних крапок для обраного критерію.

5. Якщо попадає в критичну область, то приймається альтернативна гіпотеза , якщо попадає в область прийняття гіпотези, то приймається основна гіпотеза .