5.2 Найбільш важливі розподіли, застосовувані в математичній статистиці.

5.2.1 Нормальний розподіл.

Випадкова величина , розподілена за нормальним законом, описується щільністю ймовірності:

.

Нормальний розподіл визначається двома параметрами – математичним очікуванням і середнє квадратичним відхиленим .

Випадкова величина має математичне очікування й середньоквадратичне відхилення й називається нормованою нормально розподіленою випадковою величиною . Її щільність імовірності:

,

Графік щільності розподілу наведений на малюнку 5.1.

Функція розподілу табулірована.

Імовірність влучення в інтервал :

Імовірність влучення в інтервал довжиною за правилом “ 3-х сигм” приймається за одиницю. Це рівносильне припущенню, що всі значення z укладені в інтервал .

Мал. 5.1 Графік функції щільності нормованої нормально розподіленої випадкової величини

5.2.2 Розподіл Пирсона (х2 розподіл).

Цей розподіл використовується для побудови довірчих інтервалів, перевірки відповідності емпіричного розподілу деякої теоретичної залежності, перевірки погодженості думок експертів.

Нехай є незалежних, нормованих, нормально розподілених випадкових величин . Сума їхніх квадратів утворить нову випадкову величину .

Число ступенів волі дорівнює числу незалежних доданків у сумі. Якщо на доданки накладено зв'язків, то число ступенів волі буде дорівнює .

Розподіл є нормальним і залежить тільки від числа ступенів волі . Значення табуліровані.

5.2.3 Розподіл Ст’юдєнта.

Для побудови довірчих інтервалів і для перевірки статистичних гіпотез часто використовується розподіл (розподіл Ст’юдєнта).

, де

- оцінка математичного очікування, - оцінка середнього квадратичного відхилення, розраховані за результатами досвідів, випадкової величини , розподіленої за нормальним законом з параметрами .

Розподіл Ст’юдєнта визначається числом ступенів волі , є симетричним, унімодальним і нормальним. При воно практично збігається з нормальним. Таблиця розподілу має два входи – число ступенів волі й рівень значимості . На перетинанні перебуває значення , що задовольняє умові .

5.2.4 Розподіл Фішера.

Це розподіл, як і два попередні, використовуються при аналізі результатів експерименту, що мають нормальний розподіл. - розподіл задається в такий спосіб:

,

де - випадкові величини із числом ступенів волі , причому величина в чисельнику повинна бути більше величини в знаменнику.

Шляхом тотожних перетворень приведемо, до відношення двох оцінок дисперсії деякої випадкової величини .

Нехай на основі результатів двох серій експериментів із числом досвідів відповідно були отримані - оцінки дисперсії із числом ступенів волі . Помітимо що,

,

тоді можна записати :

. Звідси .

Передбачається , що .

- розподіл визначається двома параметрами – числами ступенів волі більшої дисперсії й меншої дисперсії . Критичні значення -розподілу, що відповідають рівню значимості дані в

додатку №4. Таблиця містить значення , що задовольняють умові

0. Полігон і діаграма частот.

Полігоном частот називається ламана, з'єднуюча точки з координатами .

Якщо число різних значень велике, то в цьому випадку будується діаграма. Для цього діапазон можливих значень результатів експерименту ділиться на кілька часткових інтервалів довжиною й для кожного інтервалу підраховується число варіант , потрапивши в нього.

Діаграмою називається східчаста фігура, підстава якої дорівнює , а висота щільності частоти . Таким чином, площа фігури дорівнює числу експериментів .

Приклад 5.1

Дани спостереження значень обслідуваної ознаки:

3,0,1,4,0,7,10,1,1,1,5,8,9,6,4,3,3,7,6,4,4,4,10,9,8,1,3,0,4,9;

Треба скласти варіаційний ряд і знайти:

а) статистичний розподіл відносних частот;

б) моду, медіану, розмах варіант вибірки;

в) побудувати полігон і гістограму частот і відносних частот;

г) знайти вибіркову середню, дисперсію, середнє

квадратичне відхилення елементів вибірки.

За варіанти візьмемо спостереження значень обслідуваної ознаки. За частоти варіант візьмемо число вариант, рівних

Наприклад перша варианта зустрілась три рази, частоту покладаємо рівною . Аналогічно визначаються частоти для інших варіант. Складемо варіаційний ряд

	0	1	3	4	5	6	7	8	9	10
	3	5	4	6	1	2	2	2	3	2

За об'єм вибірки візьмемо суму частот . Отримаємо

а) Знайдемо статистичний розподіл відносних частот ( );

Складемо таблицю

	0	1	3	4	5	6	7	8	9	10
	0.1	0.16	0.13	0.2	0.033	0.067	0.067	0.067	0.1	0.067

б) Знайдемо моду цього ряду, як варіанту, що має найбільшу частоту: .

Знайдемо медіану цього ряду за формулою для парного числа варіант: , де 2m = 30; m = 15; ; .

Розмах варіант вибірки :

в) Знайдемо вибіркову середню, дисперсію, середнє квадратичне

відхилення елементів вибірки.

Вибіркова середня :

Вибіркова дисперсія :

Вибіркове середнє квадратичне відхилення

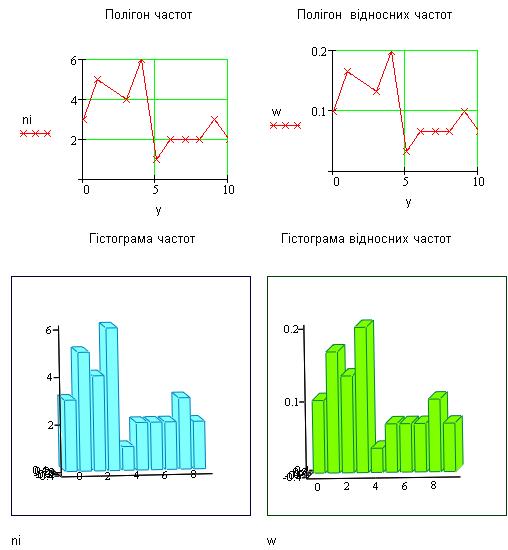Рис. 5.1 Полігон і діаграма частот та відносних частот.