5. Метод «предиктор- коректор».

Хай поставлена задача (4.1), (4.2). Послідовність наближених значень диференціального рівняння (4.1) визначається за формулами:

Спочатку за методом Ейлера визначається грубе значення наближеного рішення , а потім воно коректується. Даний метод має третій порядок точності по для локальної погрішності і другий порядок точності для глобальної погрішності.

Приклад 4.2

Знайти наближене рішення диференціального рівняння , що задовольняє умові на відрізку з кроком методом «предиктор - коректор».

1. 

2. x₂=0.2

3. x₃=0.3

Розрахунки занесемо в таблицю 4.2 :

Таблиця 4.2

	0	0.1	0.2	0.3
	1	1.1125	1.261296	1.46999

6. Вдосконалений метод Ейлера.

Хай поставлена задача (4.1), (4.2). Послідовність наближених значень диференціального рівняння визначається за формулами:

Спочатку визначається значення в середині інтервалу , потім в точці . Даний метод має третій порядок точності по для локальної погрішності і другий порядок точності для глобальної погрішності.

Приклад 4.3

Знайти наближене рішення диференціального рівняння , що задовольняє умові на відрізку з кроком вдосконаленим методом Ейлера.

1)

2)

3)

Розрахунки занесемо в таблицю 4.3 :

Таблиця 4.3

	0	0.1	0.2	0.3
	1	1.11125	1.258311	1.463442

6. Метод Рунге - Кутта

Хай поставлена задача (4.1), (4.2). Послідовність наближених значень рішень диференціального рівняння визначається за формулами:

Даний метод має п'ятий порядок точності по для локальної погрішності і четвертий порядок для глобальної погрішності.

Приклад 4.4.

За допомогою методу Рунге - Кутта, знайти наближене рішення диференціального рівняння , що задовольняє умові на відрізку з кроком .

1).

2). ;

3). ;

Розрахунки занесемо в таблицю 4.4:

Таблиця 4.4

	0	0.1	0.2	0.3
	1	1.11252	1.26207	1.47303

6. Правило Рунге для оцінки погрішності наближеного рішення диференційних рівнянь .

Хай - точне рішення задачі Коші (4.1), (4.2); - наближене рішення, знайдене на сітці . Припустимо, що на сітці справедливо: ,

де -функція, не залежна від , .

Хай - наближене рішення на сітці , тоді за правилом Рунге можна приблизно оцінити погрішність рішення на сітці

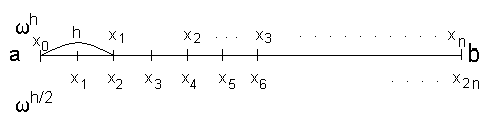
Т.ч. погрішність наближеного рішення у вузлах сітки оцінюється формулою:

Уточнене за Річардсоном рішення:

Глобальна погрішність на інтервалі :