
- •1 Основы алгебры логики
- •1.1 Понятие о логических функциях
- •Функции одной и двух переменных
- •2.1Булевы функции одной переменной
- •Булевы функции двух переменных
- •2.3 Понятие базиса и функционально-полного базиса
- •Основные аксиомы и тождества алгебры логики
- •Способы задания Булевых функций
- •3.1 Описательный способ:
- •3.2 Аналитический метод:
- •3.2.1Совершенная дизъюнктивная нормальная форма (сднф)
- •3.2.2 Совершенная конъюнктивная нормальная форма (скнф)
- •3.2.3Таблица истинности и последовательность значений наборов переменных
- •3.2.4 Геометрический способ представления функций алгебры логики (фал) (кубические комплексы)
- •3.2.5 Временные диаграммы
- •3.2.6 Функциональные схемы
- •3.2.7 Взаимные преобразования способов представления фал
- •4. Основные характеристики и параметры логических элементов
- •4.1 Цифровые устройства и их классификация (из инета)
- •4.2 Передаточные характеристики
- •4.3 Входная характеристика
- •4.4 Выходная характеристика
- •4.5 Нагрузочная способность
- •5. Базовые логические элементы
- •5.1 Структура логических элементов
- •5.1.1 Логические устройства диодной логики
- •5.1.2 Простой усилительно-формирующий каскад
- •5.1.3Сложный усилительно-формирующий каскад (двухтактный)
- •5.2 Базовый элемент ттл-логики
- •5.2.5 Модификации базовых элементов
- •5.3 Ттлш-логический элемент
- •5.3 Базовые элементы кмоп логики, преимущества
- •6. Синтез комбинационных устройств
- •6.1 Основные этапы неавтоматизированного синтеза комбинационных устройств.
- •6.2 Минимизация цифровых устройств
- •6.2.1 Аналитическая минимизация фал
- •6.2.2 Минимизация фал на основе карт Карно
- •6.2.3 Смысл и применимость методов минимизации при синтезе цифровых устройств.
- •6.3 Приведение фал к заданному базису.(и-не, или-не, и-или-не)
- •Типовые комбинационные устройства
- •7.1 Типовые комбинационные цифровые устройства.
- •Преобразователи кодов
- •Шифраторы (кодеры) и дешифраторы (декодеры)
- •Мультиплексоры и демультиплексоры (Концентраторы)
- •7.5 Сумматоры
- •Компараторы кодов
- •8 Последовательностные устройства
- •8.1 Обобщённая схема последовательностного устройства
- •8.2 Понятие об автоматах Мили и Мура
- •9 Триггеры
- •9.1 Классификация
- •9.2.1 Асинхронный rs-триггер
- •9.2.2 Синхронизируемый уровнем
- •9.2.4 Двухтактный rs-триггер
- •9.3.1 Асинхронный d–триггер
- •9.3.4 Двухтактный d–триггер
- •9.4.1 Асинхронный
- •9.4.3 Синхронизируемый фронтом jk-триггер
- •9.4.4 Двухтактный jk-триггер
- •10. Типовые последовательностные устройства
- •10.1 Регистры
- •10.1.1 Классификация
- •10.2 Счетчики.
- •10.2.1 Классификация счетчиков.
- •10.2.3 Асинхронные двоичные счётчики
- •10.2.4 Суммирующие. Схема. Быстродействие
- •10.2.5 Вычитающий счетчик. Схема. Быстродействие.
- •10.2.6 Реверсивные счетчики
- •10.2.8 Счётчики с параллельным переносом
- •10.2.9 Счетчик с групповым переносом.
- •10 .3 Генератор чисел
- •10.4 Распределители импульсов
- •11.Цифрово-аналоговые преобразователи
- •11.1 Классификация цап
- •12 Аналого-цифровые преобразователи (ацп). Методы построения.
- •Параллельные ацп
- •Последовательно-параллельные ацп
- •Ацп последовательного приближения
- •Интегрирующие(равертывающего) ацп
- •Следящие ацп:
- •Сигма-дельта ацп
- •Тема 13. Общие принципы построения и функционирования компьютеров
- •13Машина фон Неймана
- •13.1.2 Машины Гарвардского и Принстонского классов
- •13.2 Организация памяти эвм
- •13.3 Микропроцессоры
- •Интерфейсы эвм
- •Общая организация систем обработки данных как совокупности аппаратных и программных средств.
- •14 Локальные и глобальные вычислительные сети.
- •15 Проблемы безопасности компьютерных сетей
10.2 Счетчики.
Последовательное устройство циклически переходящее из одного состояния в другое под действием сигнала, подаваемого на один вход, называется счётчиком.
Счетчики выполняют на запоминающих элементах – триггерах. Он фиксирует число импульсов, поступивших на его вход. В интервалах между ними счетчик хранит информацию об их числе. Совокупность единиц и нулей на выходах n триггеров (выходах счетчика) представляет собой n-разрядное двоичное число, однозначно определяющее количество прошедших на входе импульсов. Поэтому триггеры счетчика называют его разрядами.
Количество входных переключающих сигналов необходимых для перевода счётчика в исходное состояние называется коэффициентом пересчёта ( модулем счёта ).
Счётчики с наиболее
распространёнными модулями счёта имеют
специальные названия. Счётчик по модулю
 -
двоичный , а
-
двоичный , а
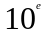 -
десятичный .
-
десятичный .
10.2.1 Классификация счетчиков.

1) По значению модуля счёта различают двоичные (М=2n), двоично-кодированные (с произвольным модулем, но кодированием состояний двоичными кодами), счётчики с одинарным кодированием и др.
2) По направлению счёта счётчики делят на суммирующие (прямого счёта), вычитающие (обратного счёта) и реверсивные (с изменением направления счёта).
3) По способу организации межразрядных связей различают счётчики с последовательным, параллельным и комбинированными переносами. Параллельные счётчики называют синхронными, а последовательные - асинхронными.
Задать счётчик, значит задать последовательность переходов его из одного состояния в другое.
Основными параметрами счетчика являются:
модуль счета или коэффициент пересчета Ксч;
Модуль счета Ксч характеризует число устойчивых состояний счетчика, т. е. предельное число импульсов, которое может быть им сосчитано. После поступления Ксч входных импульсов счетчик возвращается в исходное состояние. Такие счетчики называются также делителями на число, равное Ксч.. По модулю счета счетчики подразделяются на двоичные, у которых Ксч=2m, и недвоичные, у которых Ксч¹2m, где m – положительное целое число.
быстродействие счетчика.
Быстродействие счетчика в свою очередь определяется двумя величинами:
разрешающей способностью, т.е. минимальным допустимым интервалом времени между подачей двух входных импульсов, при котором не происходит потеря счета;
временем установки tуст кода счетчика, т.е. интервалом времени между моментом поступления входного сигнала и моментом завершения перехода счетчика в новое устойчивое состояние.
При этом должно выполняться условие tр>tуст.
10.2.3 Асинхронные двоичные счётчики
Наиболее просты счётчики по модулю
Такой счётчик описывается следующим выражением

Qn-1+1 при Qn-1 2m-1
Qn=0 при Qn-1=2m-1
При небольшом модуле можно пользоваться таблицей переключений:
-
A



0
1
2
3
4
5
6
7
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
Из таблицы видно, что каждый из р. счётчиков есть Т-триггер.

В свою очередь Т-триггер можно реализовать на базе D или J-К синхронного триггера.

Т.к. переключающий сигнал – переходит из 0 в 1, то на следующий триггер он подаётся с инверсного выхода предыдущего триггера.
Вычитающий счётчик функционирует по выражению:
 при
при
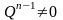
 =
=
 при
при

Легко понять, что он будет отличаться от суммирующего лишь способом соединения триггеров (сигнал на последующий триггер берётся с прямого выхода предыдущего).

Возможно и построение реверсивного двойного счётчика с последовательным переносом. При этом нужно предусмотреть возможность изменения направления счёта таким образом, чтобы не вызвать в схеме лишнего переключения фронтом коммутирующего сигнала.
Сигнал на вход следующего счётчика при этом будет определяться следующим образом.



 =
=






Несколько сложнее счётчики с модулем счёта М<2к в этом случае возникает задача устранения лишних состояний - 2к –М. Это может осуществляться либо сбросом счётчика при достижении заданного состояния в начальное состояние, либо предварительной установкой в начальное состояние, код которого равен числу лишних состояний.
По первому способу определяется количество триггеров в схеме
 ,
,
Строится обычный последовательный счётчик и комбинационной схемой формируется сигнал сброса в начальное состояние.
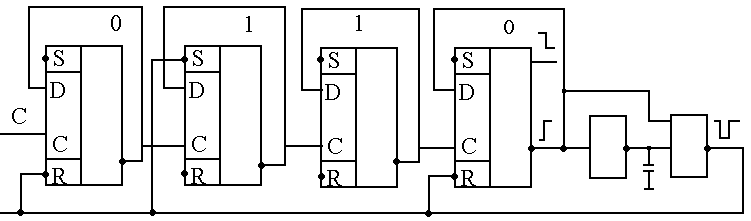
Пример. М=10
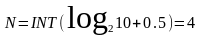
код, по которому схема должна вернуться в исходное состояние М=10 – 1010

Четыре последовательно включенных инвертора позволяют увеличить время воздействия импульса сброса и добиться установления в начальное состояние всех триггеров. Состояние 1010 является промежуточным. Длительность импульса сброса должна быть меньше периода следования счетных импульсов.
Синтез счетчика с предустановкой покажем на том же примере. Код предварительной установки 24-10=6 0110. Схема на двух инверторах – формирователь отрицательного импульса выделяемого из спада импульса последнего триггера. Последовательность пробегаемых кодов в этой схеме


 0110, 0111, 1000, 1001, 1010, 1011, 1100, 1101,
1110, 1111
0110, 0111, 1000, 1001, 1010, 1011, 1100, 1101,
1110, 1111
Данный вариант схемы неудобен тем, что последовательность кодов не дешифруется стандартным дешифратором 410.
Основной характеристикой счётчика является разрешающее время счётчика – время соответсвующее максимальной частоте счёта. Для счётчиков с последовательным переносом.

 - время разрешения первого триггера.
- время разрешения первого триггера.
 -
задержка триггера.
-
задержка триггера.
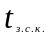 -
задержка схемы коммутации ( для реверс.
счётчика)
-
задержка схемы коммутации ( для реверс.
счётчика)
 -
минимально-необходимая длительность
состояния.
-
минимально-необходимая длительность
состояния.
Выходной сигнал с последнего триггера счётчика имеет частоту следования в М раз меньшую. Здесь следует отметить, что двоичные счётчики, как и счётчики с произвольным модулем счёта имеют быстродействие, определяемое приведённой выше формулой. Однако, если такой счётчик используется как делитель частоты, то максимальная частота, подаваемая на его вход, равна максимальной рабочей частоте триггера.
