
- •Числовой ряд. Частичная сумма ряда. Сходящиеся и расходящиеся ряды. Необходимый признак сходимости.
- •Свойства числовых рядов.
- •Признаки сравнения рядов с положительными членами.
- •Признак Даламбера.
- •Радикальный признак Коши.
- •Интегральный признак Коши. Ряд Дирихле.
- •Знакопеременный ряд. Его признак сходимости. Понятие об условной и абсолютной сходимости.
- •Знакочередующиеся ряды. Признак Лейбница.
- •Функциональный ряд. Область сходимости функционального ряда. Остаточный член сходящегося функционального ряда.
- •11.Формулы Тейлора и Маклорена с остаточным членом в форме Логранджа.
- •12.Формулы Тейлора и Маклорена. Ряд Маклорена для функции (с нахождение области сходимости этого ряда).
- •13.Ряды Маклорена для функций sin X и cos X (c нахождением области сходимости).
- •14.Теорема Абеля для степенных рядов. Интервал и радиус сходимости степенного ряда, его область сходимости.
- •15.Биноминальный ряд, его область сходимости.
- •16.Степенные ряды для функций
- •17.Разложение в ряд Маклорена функций arcsin X, arctg X.
- •19.Производная от определенного интеграла по переменному верхнему пределу. Формула Ньютона-Лейбница.
- •21. Несобственные интегралы.
- •22.Функции нескольких переменных. Графическое задание функции двух переменных.
- •23.Предел функции двух переменных. Частное и полное приращение. Частные производные.
- •24. Выражение полного приращения функции через частные производные. Полный дифференциал.
- •25. Дифференциальные уравнения полных дифференциалов. Дифференциальные уравнения первого порядка неразрешенные относительно одной производной.
- •26. Производная сложной функции нескольких переменных. Полная производная
- •27. Точка максимума и минимума функции двух переменных.
- •28. Необходимые условия экстремума. Достаточное условие для функции двух переменных
- •29. Метод наименьших квадратов.
- •30. Производная по направлению
- •31. Градиент.
- •32. Понятие двойного интеграла, его свойства вытекающие из определения.
- •35. Двойной интеграл в полярных координатах. Двойной интеграл Пуассона.
- •36.Тройной интеграл и его вычисление с помощью трехкратного
- •37. Тройной интеграл в цилиндрических координатах.
- •38. Тройной интеграл в сферических координатах.
35. Двойной интеграл в полярных координатах. Двойной интеграл Пуассона.
Одним из частных
случаев замены переменных является
переход из декартовой в полярную систему
координат (рисунок 1).
![]()

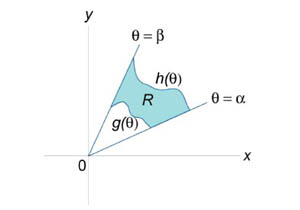
Рис.1 Рис.2
Якобиан такого
преобразования имеет вид
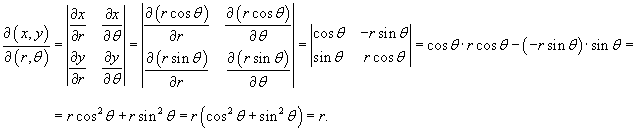 Следовательно, дифференциальный элемент
в полярных координатах будет равен
Следовательно, дифференциальный элемент
в полярных координатах будет равен

Гауссов интеграл
(также интеграл Эйлера — Пуассона или
интеграл Пуассона) — интеграл от
гауссовой функции:
![]()
36.Тройной интеграл и его вычисление с помощью трехкратного


37. Тройной интеграл в цилиндрических координатах.
В цилиндрических координатах положение точки M(x,y,z) в пространстве Oxyz определяется тремя числами − ρ, φ, z , где ρ − длина радиуса-вектора проекции точки M на плоскость Oxy, φ − угол, образованный этим радиусом-вектором с осью Ox (рисунок 1), z − проекция на ось Oz (ее значение одинаково в декартовых и цилиндрических координатах).

Рис.1
Цилиндрические координаты точки связаны с ее декартовыми координатами соотношениями
![]()
Здесь предполагается,
что
![]()
Якобиан перехода от декартовых координат к цилиндрическим равен

Тогда формула замены переменных при данном преобразовании имеет вид:
![]()
Переход к цилиндрическим координатам упрощает вычисление тройного интеграла в случаях, когда область интегрирования образована цилиндрической поверхностью.
38. Тройной интеграл в сферических координатах.
Рассмотрим сферическую систему координат ОρΘφ, совмещённую с декартовой системой Оxyz. При этом максимальные пределы изменения сферических координат таковы: 0 ≤ φ ≤ 2π, 0 ≤ ρ ≤ ∞

Из рис. 2.21 нетрудно вывести следующие формулы, связывающие декартовые и сферические координаты:

с помощью которых получим Якобиан преобразования:

Таким образом, переход к сферическим координатам в тройном интеграле осуществляется по формулам:
