
- •Общие понятия об инженерных сетях и сооружениях и их роли и значении в экономике страны.
- •2. Физические свойства жидкостей.
- •3.Гидростатическое давление
- •4.Атмосферное давление
- •5 .Давление абсолютное, избыточное и разряжение(вакуум)
- •7) Основные характеристики движения жидкостей
- •8. Скорость и расход жидкости
- •9) Уравнение неразрывности потока
- •10. Материальный баланс потока(уравнение неразрывности потока)
- •11.Уравнение бернулли (энергетический баланс потока)
- •12. Режимы движения жидкости
- •13. Распределение скоростей по сечению потока при ламинарном режиме
- •14. Некоторые практические приложения уравнения бернулли
- •15. Движение жидкости в напорных трубопроводах и их расчет
- •16. Трубопроводы. Классификация
- •17. Типы соединения труб
- •18. Классификация трубопроводной арматуры
- •19. Типы трубопроводной арматуры
- •20. Конструкции насоса
- •22. Характеристики трубопровода. Совместная работа насос-трубопровод.
- •23. Типовые закономерности насоса
- •24. Последовательно и параллельновключённые насосы
- •25. Объемные насосы
- •26 Струйный насос
- •27. Эрлифт (газлифт)
- •28. Метод анализа ст-ти lc при выборе оптим насос об-ния
- •29. Структура стоимости жизн цикла
- •30. Системы и схемы питьевого водоснабжения
- •31. Классификация систем водоснабжения.
- •I .По степени централизации
- •II .По предназначению
- •III .По степени охвата нужд водопотребителей
- •IV.По способу подачи и распределения воды
- •32. Водопотребление и требуемое давление
- •33.Водозаборные сооружения из подземных источников
- •34. Водозаборные сооружения из поверхностных источников
- •35.Показатели качества воды
- •1)Водородный показатель (рН, ед рН)
- •2)Общая жесткость
- •7)Железо
- •8)Марганец
- •9)Окисляемость перманганатная
- •18)Алюминий
- •36.Основные процессы обработки воды
- •37.Осветление воды в фильтрах
- •38. Обеззараживание воды
- •40. Особенности систем водоотведения (канализации)
- •41. Сточные воды, понятие и классификация
- •42. Системы и схемы канализации
- •43. Канализационные сети
- •44. Сооружения очистки сточных вод.
- •45. Схемы внутренней канализации здания и дворовой внутриквартальной канализационной сети
- •46.Биологическая очистка сточных вод
- •47. Механическая очистка сточных вод
- •48. Сооружения обработки осадка сточных вод
- •49. Способы теплоснабжения.
- •50. Основные виды и схемы централизованного теплоснабжения водяные системы теплоснабжения.
- •51. Тепловые сети: их назначение, конструкции.
- •52. Котельные: назначение, классификация, параметры.
- •53. Газы и их добыча.
- •54. Основные элементы систем газоснабжения.
- •55. Классификация газопроводов.
- •56. Классификация газовых сетей.
- •57. Газовые распределительные сети.
- •58. Системы и схемы газоснабжения.
- •59. Устройство и оборудование газовых сетей.
- •61. Источник тока. Электростанции.
- •62. Схемы электрической сети
- •5. По роду тока и числу проводов:
- •6. По режиму работы нейтрали:
- •7. По схеме электрических соединений:
- •8. По конструкции:
- •64. Требования, предъявляемые к электрическим сетям
- •65. Внутренние электрические сети
8. Скорость и расход жидкости
Расход - количество жидкости, протекающее через живое сечение потока в единицу времени
Массовый
m и объемный Q расходы связаны соотношением:
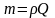
Если
расход жидкости через поперечное сечение
ΔFi элементарной струйки составляет ΔQ,
то средняя скорость жидкости в данном
сечении wi равна
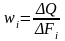
Общий
расход потока:
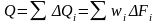
Средняя
скорость потока:
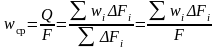
Массовая
скорость потока:
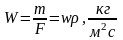

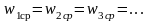 равномерное
движение
равномерное
движение
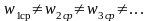 неравномерное
движение
неравномерное
движение

Одномерное двумерное трехмерное
(линейное) (плоское) (пространственное)
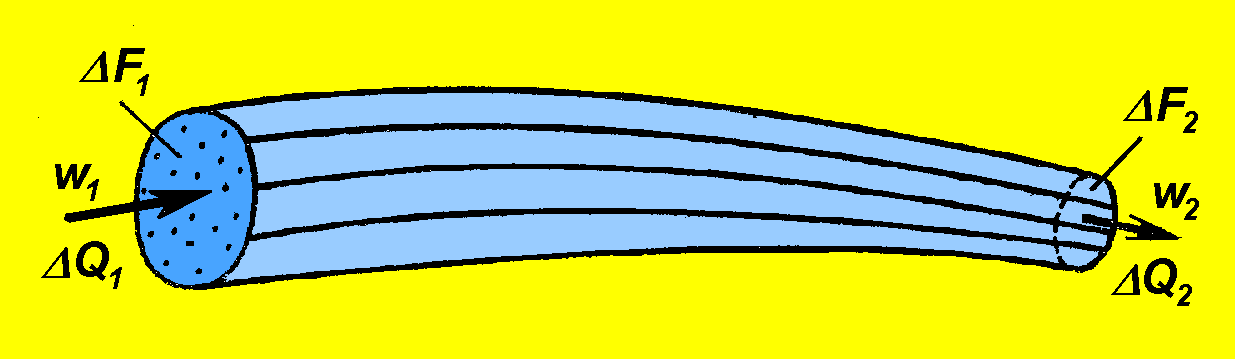
9) Уравнение неразрывности потока
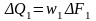
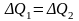
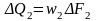
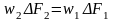
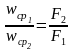
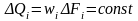 - уравнение
неразрывности струи
- уравнение
неразрывности струи
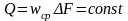 - уравнение
неразрывности потока
- уравнение
неразрывности потока
10. Материальный баланс потока(уравнение неразрывности потока)
w-скорость движения слоя жидкости;
∆F-площадка слоя (площадь, поперечное сечение);
∆Q-расход жидкости.
- уравнение неразрывности струи
- уравнение неразрывности потока
Закон: При установившемся движении расход в любом сечении одинаков, скорости разные.
11.Уравнение бернулли (энергетический баланс потока)
Энергия жидкости включает три составляющих:
1.Внутреннюю энергию:
1.1.Кинетическая энергия движения молекул
1.2.Потенциальная энергия межмолекулярного притяжения
1.3. Энергия внутримолекулярных колебаний
2.Потенциальную:
2.1.Энергия давления Пр=pV
2.2.Энергия положения Пz=Gz=mgz
3.Кинетическую K=mw2/2
Полная энергия жидкости: E’=U+pV+mgz+mw2/2, Дж
Удельная энергия жидкости: E=u+pγ+gz+w2/2, Дж/кг
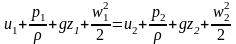
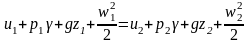
, u1=u2
 -
уравнение
Бернулли
для
идеальной жидкости
-
уравнение
Бернулли
для
идеальной жидкости
У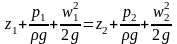 равнение
Бернулли является
частным
случаем закона сохранения энергии и
выражает
энергетический
баланс потока:
полная удельная энергия жидкости есть
величина постоянная во всех сечениях
потока.
равнение
Бернулли является
частным
случаем закона сохранения энергии и
выражает
энергетический
баланс потока:
полная удельная энергия жидкости есть
величина постоянная во всех сечениях
потока.
E=Hg
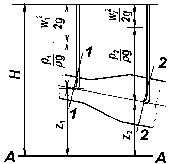
Полный напор Н - энергия жидкости, отнесенная к единице силы тяжести
z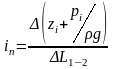
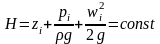 i-геометрический
напор
i-геометрический
напор
pi/(ρg)-пьезометрический напор
wi2/(2g)-скоростной напор
пьезометрический уклон.
В
отличие от идеальной жидкости, для
которой полный напор Н
= const,
для реальной жидкости полный
напор убывает по направлению д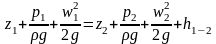 вижения
жидкости.
вижения
жидкости.
-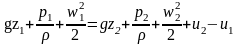 уравнение
Бернулли
для
реальной
жидкости
уравнение
Бернулли
для
реальной
жидкости
Из уравнения Бернулли следует, что увеличение скоростного напора сопровождается соответствующим уменьшением пьезометрического напора и наоборот.
H1=H2+h1-2
h1-2=(u2-u1)/g –потери напора между 1м и 2м сечениями из-за расширения и сил трения
i=∆H/∆L1-2 –гидравлический уклон.
Потери напора h1-2 на преодоление сопротивлений движению жидкости состоит из линейных hл и местных hм сопротивлений.
Линейные сопротивления связаны с протяженностью потока жидкости и обусловлены трением частиц одна о другую и стенки канала (трубопровода).
Местные сопротивления вызываются различными препятствиями на пути движения потока в виде задвижек, вентилей, поворотов, сужений и расширений сечения и т.п.
12. Режимы движения жидкости
Опыт Рейнольдса. 1883г
1 – сосуд
2 - стеклянная труба
3 - капиллярная трубка
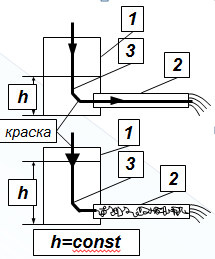
пути частиц прямолинейны и параллельны друг другу
ламинарное движение (слой)
частицы жидкости движутся по хаотическим траекториям
турбулентное движение (хаотичное)
Опыт показывает, что переход от ламинарного течения к турбулентному зависит от массовой скорости жидкости ρw, диаметра трубы d и вязкости жидкости μ.
Критерий Рейнольдса: Reкр=2300
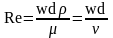
Re < 2300 – устойчивый ламинарный режим
2300 < Re < 10000 – неустойчиво турбулентный режим
Re > 10000 – устойчиво турбулентный режим
