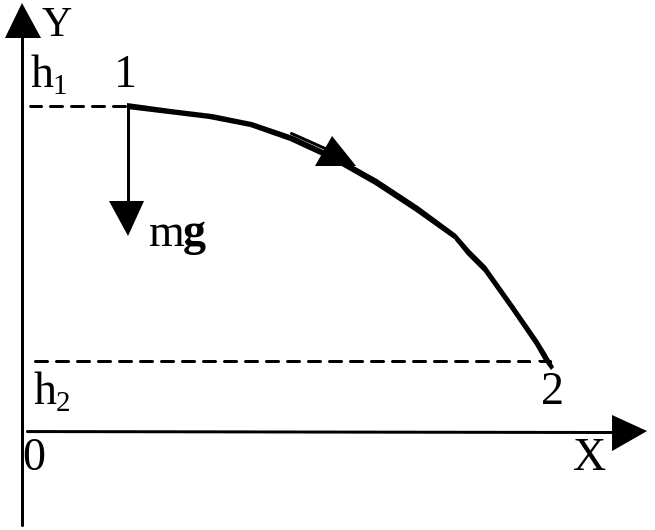
10. Работа и энергия упругих сил и сил тяготения. Потенциальная

энергия тела, поднятого над землей.

1) Сила тяжести:

А₁₂ = Fdr = - mgdу = mgh₁ - mgh₂ = Е_п1 - Е_п2 = - Е_п

• Е_п = mgh + const

2) Сила упругости:

А₁₂ = Fdr = -kхdх = kх₁²2 - kх₂²2 = Е_п1 - Е_п2 = -Е_п, где Е _п = kх²2 + const

Из приводимых выше формул видно, что, измеряя работу потенциальных сил, можно найти только разность потенциальных энергий, то есть сама потенциальная энергия определяется неоднозначно, а именно - с точностью до константы.

Работа консервативных сил совершается за счет убыли потенциальной энергии (энергии взаимодействия) и идёт на приращение кинетической энергии тела (энергии движения):

А₁₂ = Е_к = - Е_п или Е_к2 - Е_к1 = Е_п1 - Е_п2  Е_к1 + Е_п1= Е_к2 + Е_п2

11. Консервативные и неконсервативные силы. Закон сохранения энергии в механике

Консервативные силы – силы, работа которых не зависит от формы траектории по которой движется тело и определяется в начальной и конечной точках траектории; работа этих сил по замкнутому контуру = 0 Диссипатиыные силы – силы, работа которых зависит от формы траектории по кторой движется тело. Полная механическая энергия тела, т. е. сумма кинетической и потенциальной энергий, остается при его движении под действием консервативных сил неизменной, т. е. сохраняется. Она может лишь переходить в эквивалентных количествах из одного вида (энергии движения) в другой (энергию взаимо­действия) и наоборот. Это утверждение и представляет собой суть закона сохранения энергии замкнутой консервативной механической системы (ЗСМЭ)

12. Момент инерции материальной точки. Момент инерции тела. При-

вести примеры. Теорема Штейнера.

Основное уравнение М_z = J_z динамики вращательного движения твердого тела (системы материальных точек) относительно неподвижной оси по своей структуре идентично второму закону Ньютона F = mа. Аналогом массы m в нем выступает момент инерции J твердого тела. И так же, как масса, он выступает мерой инертности тела, но применительно к вращательному движению. Чем больше момент инерции J твердого тела, тем меньшее угловое ускорение  оно приобретает под действием одного и того же момента М внешних сил, то есть тем медленнее изменяется его угловая скорость. Момент инерции материальной точки J_ = m_r_² пропорционален квадрату расстояния r_ от точки до оси вращения. С ростом массы m и при неизменном расстоянии r до оси вращения, та же сила F сообщает материальной точке меньшее линейное ускорение (по 2-му закону Ньютона), а соответственно и угловое ускорение  = аr. С удалением точки от оси враще­ния возрастает момент М одной и той же силы F: М = Fr и уменьшается угловое ускорение  = аr = Fmr, а момент инерции J = М/ = Fr(Fmr) = mr² возрастает квадратично расстоянию до оси вращения (радиусу окружности). Момент инерции, как и масса тел, оказывается аддитивной характеристикой, то есть результирующий момент инерции твёрдого тела (системы матери­альных точек) равен сумме моментов инерции составляющих его частиц:

J = J_к = m_кr_к²

В случае непрерывного распределения точек /массы/ сумма в выражении для момента инерции заменяется интегралом: J = r_к²dm = r²dV

Момент инерции тела зависит не только от его массы, но и от её распре­деления относительно оси вращения. Для некоторых симметричных и однород­ных тел момент инерции J_с относительно оси, проходящей через центр симметрии С (центр масс или центр инерции) выражается следующими формулами:

1. Колесо /обод/, полый цилиндр: J_с = mR²

2. Диск, сплошной цилиндр: J_с = mR²2

3. Шар: J_с = 2mR²5

4. Стержень: J_с = ml²12

При параллельном переносе оси вращения на расстояние а от центра инерции момент инерции тела массой m возрастает на mа², т. е. J = J_С + mа². В этом состоит суть теоремы Штейнера. Выведем эту теорему.

Дано твердое тело (система материальных точек).

Проведем две параллельные оси; одну через центр масс С тела и другую через точку О, отстоящую от центра масс на расстояние а. На рисунке оси перпендикулярны плоскости чертежа. Выделим в твердом теле некоторую элементарную массу m_. Проведем в нее из точек С и О векторы R_ и r_.

Из чертежа видно, что r_ = а + R_. Возведем это равенство в квадрат: r_² = а² + 2аr_ + R_². Умножим его на m_ и просуммируем по всем элементарным массам (точкам) тела: m_r_² = а²m_ + 2аm_R_ + m_R_².

Первая сумма m_r_² в полученном равенстве представляет собой момент инерции J тела относительно точки О, а последняя сумма m_R_² представляет собой момент инерции J_С тела относительно центра масс. Так как m_ равна массе m всего тела, то слагаемое а²m_ = mа². И, наконец, вспоминая определение радиус-вектора центра масс:

R_С = (1/m)m_R_, видим, что сумма m_R_ = mR_С представляет собой произведение массы тела на радиус-вектор R_С центра масс тела. Но так как здесь радиус-вектор R_С задается относительно самого центра масс, то он получается равным нулю. В итоге написанное выше равенство примет вид J = mа² + J_С, который и представляет собой теорему Штейнера.