№1 Множества и действия над ними. Свойства операций над множествами.

Множество - Одно из основных и сходных понятий математики. множество состои из элементов. если элемент а принадлежит множеству М, это записывается как , иначе как или .

Множество А называется подмножеством М если всякий элемент А является элементом М. обозначается .при этом говорят, что М содержит или покрывает А.

Множества А и М равны, если их элементы совпадают. Или, в формульном виде, соледующие две записи верны:

Если и , то А называется собственным, строгим или истиным подмножеством М и можно обозначить как

Множество бывают конечные и бесконечные.

Мощность множества - это количество его элементов. обозночается |M|

множество мощности 0 называется пустым

множество задаются разными способами:

1) списком (A={1,2,3,4})

2) Порождающей процедурой( , если то (или иным другим способом, указывающим процедуру и необходимые данные для её подсчёта))

3) описанием свойств оего элементов (M - множество целых степеней двойки)

Действия над множествами

Объединение множеств - множество, включающее в себя все элементы множества А и множества М. Обозначается . Условно можно записать как если или . объединение N множеств - аналогично.

Пересечение множеств А и М - множество, содержащее всебе элементы, присутствующие и в А и в М . Обозначается если и

разность множеств А и М - множество только тех элементов, которые есть в А но отсутствуют в М. Обозначается если и . Если А\В= (пустое множество) , то . от перемены мест множеств результат меняется! Известна как операция дополнения A до U.

Симметричная разность множеств А и М - Множество, состоящее из элементов, существующих тольков в одном из данных множеств. обозначается А М ={x если x }

Прямое произведение А и М - множество, состоящие из пар (a,m) таких, что и . обозначается

Операции над множествами

функция вида называется n-арной операцией на множестве М

операция ассоциативна.

операция коммутативна.

так же существуют свойство, верные не для всех операций.

операция называется дистрибитивно слева относительно операции если

операция называется дистрибитивно справа относительно операции если

Отображения множеств

понятие отоброжения множеств неразрывно связано с понятием функции. Функцией называют функциональное соответствие. Если функция f устанавливает соответствие между множествами А и В, то соответствует единственное (более привычная форма - f(a)=b ). обозначается как

Полностью заданная функция называется отображением множества А на множество В.

№2 формула включений и исключений для подсчёта числа элементов в объединении множеств.ь

№3 Комбинаторные Объектыи комбинаторные числа. Выборки и их виды.

№4 Правила комбинаторики, их теоретик-множественная трактовка.

№5 Размещение без повторений

Обозначается или

Или

№6 Размещение с повторением

Размещение с повторениями или выборка с возвращением — это размещение «предметов» в предположении, что каждый «предмет» может участвовать в размещении несколько раз. Обозночается или По правилу умножения количество размещений с повторениями из n по k равно

Например, количество вариантов 3-x значного кода, в котором каждый знак является цифрой от 0 до 9 и может повторяться, равно:

№6 Размещение с повторением

Размещение с повторениями или выборка с возвращением — это размещение «предметов» в предположении, что каждый «предмет» может участвовать в размещении несколько раз. По правилу умножения количество размещений с повторениями из n по k равно

Например, количество вариантов 3-x значного кода, в котором каждый знак является цифрой от 0 до 9 и может повторяться, равно:

№7 Сочетание без повторений

В комбинаторике сочетанием из n по k называется набор k элементов, выбранных из данных n элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.

№8 Сочетание с повторениями

№9 Перестановки и подсчет их количества

Число всех перестановок порядка n равно числу 0%A0%D0%B0%D0%B7%D0%BC%D0%B5%D1%89%D0%B5%D0%BD%D0%B8%D1%8F"размещений из n по n, то есть 0%A4%D0%B0%D0%BA%D1%82%D0%BE%D1%80%D0%B8%D0%B0%D0%BB"факториалу:

№10 Формула Бинома Ньютона, подсчет числа возможных подмножеств конечного множества

Бином Ньютона — формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных, имеющая вид

,

где   — 0%91%D0%B8%D0%BD%D0%BE%D0%BC%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D1%8B%D0%B9_%D0%BA%D0%BE%D1%8D%D1%84%D1%84%D0%B8%D1%86%D0%B8%D0%B5%D0%BD%D1%82"биномиальные коэффициенты, n — неотрицательное 0%A6%D0%B5%D0%BB%D0%BE%D0%B5_%D1%87%D0%B8%D1%81%D0%BB%D0%BE"целое число.

Докажем это равенство индукцией по n:

База индукции: n = 1

(a + b)¹ = a + b

Шаг индукции: Пусть утверждение для n верно:

Тогда надо доказать утверждение для n + 1:

Начнём доказательство:

Извлечём из первой суммы слагаемое при k = 0

Извлечём из второй суммы слагаемое при k = n

Теперь сложим преобразованные суммы:

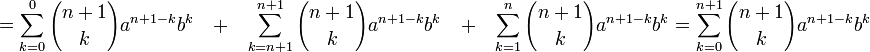
№11 Полиноминальные коэффициенты

Мультиномиальные (полиномиальные) коэффициенты — коэффициенты в разложении   по мономам  :

Значение мультиномиального коэффициента   определено для всех целых неотрицательных чисел n и   таких, что  :

Биномиальный коэффициент   для неотрицательных целых чисел n, k является частным случаем мультиномиального коэффициента (для m = 2), а именно

В комбинаторном смысле мультиномиальный коэффициент   равен числу упорядоченных разбиений n-элементного 0%9C%D0%BD%D0%BE%D0%B6%D0%B5%D1%81%D1%82%D0%B2%D0%BE"множества на m подмножеств мощностей  .

Свойства

№12 Свойства биноминальных коэффициентов. Треугольник Паскаля

Треугольник Паскаля — арифметический треугольник, образованный биномиальными коэффициентами. Назван в честь Блеза Паскаля.

Если очертить треугольник Паскаля, то получится равнобедренный треугольник. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Продолжать треугольник можно бесконечно. Строки треугольника симметричны относительно вертикальной оси. Имеет применение в теории вероятностей и обладает занимательными свойствами.

№13 Принцип включения и исключения и его применение к решению комбинаторных задач на примере задачи о беспорядках.

Классический пример использования формулы включений-исключений — задача о беспорядках. Требуется найти число перестановок   множества   таких что   для всех  . Такие перестановки называются беспорядками.

Пусть   — множество всех перестановок   и пусть свойство   перестановки выражается равенством  . Тогда число беспорядков есть  . Легко видеть, что   — число перестановок, оставляющих на месте элементы  , и таким образом сумма  содержит   одинаковых слагаемых. Формула включений-исключений дает выражение для числа   беспорядков:

Это соотношение можно преобразовать к виду

Нетрудно видеть, что выражение в скобках является частичной суммой ряда  . Таким образом, с хорошей точностью число беспорядков составляет  долю от общего числа   перестановок:

№14 Рекуррентные соотношения, соответствующие им рекуррентные уравнения и их решения. Понятие характеристического многочлена.

Линейной рекуррентной последовательностью (линейной рекуррентой) называется всякая числовая рекуррентная последовательность  , задаваемая линейным рекуррентным соотношением:

 при 

с заданными начальными членами  , где n — фиксированное натуральное число,   — заданные числовые коэффициенты,  . При этом числоn называется порядком последовательности.

Линейные рекуррентные последовательности иногда называют также возвратными последовательностями.

Для линейных рекуррентных последовательностей существует формула, выражающая общий член последовательности через корни её характеристического многочлена

Для чисел Фибоначчи такой формулой является формула Бине.

Пример

Для последовательности  , удовлетворяющей линейному рекуррентному уравнению второго порядка   с начальными значениями  ,  , справедлива формула:

.

Для того, чтобы найти   необходимо решить характеристическое уравнение  . Если дискриминант этого уравнения отличен от нуля, то

где   — любой из двух корней этого уравнения. Если же дискриминант характеристического уравнения равен нулю, то

В частности, для последовательности, определяемой следующим линейным рекуррентным уравнением второго порядка

;  ,  .

корнями характеристического уравнения   являются  ,  . Поэтому

.

Окончательно:

№15 Нахождение решений линейного однородного рекуррентного уравнения второго порядка. Нахождение чисел Фибаначи.

Формула Бине выражает в явном виде значение F_n как функцию от n:

,

где   — золотое сечение. При этом   и   являются корнями характеристического уравнения  .

Из формулы Бине следует, что для всех  , F_n есть ближайшее к   целое число, то есть  . В частности, при   справедлива асимптотика  .

Формула Бине может быть аналитически продолжена следующим образом:

При этом соотношение F_{z + 2} = F_{z + 1} + F_z выполняется для любого комплексного числа z.

№16 Отношения на множествах. Свойства отношений. Отношение эквивалентности и классы эквивалентности. Разбиение множеств.

Отношение эквивалентности (∼) на множестве X — это бинарное отношение, для которого выполнены следующие условия:

• Рефлексивность: 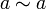  для любого a в X,

• Симметричность: если  , то  ,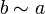

• Транзитивность: если   и  , то  .

Запись вида « » читается как «a эквивалентно b».

• Классом эквивалентности C(a) элемента a называется подмножество элементов, эквивалентных a. Из вышеприведённого определения немедленно следует, что, если 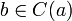 , то C(a) = C(b).

Множество всех классов эквивалентности обозначается X / ∼.

• Для класса эквивалентности элемента a используются следующие обозначения: [a], a / ∼,  .

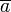• Множество классов эквивалентности по отношению ∼ является разбиением множества.

• Равенство (« »), тривиальное отношение эквивалентности на любом множестве, в частности, вещественных чисел.

• Сравнение по модулю, («а ≡ b (mod n)»).

• В Евклидовой геометрии

• Отношение конгруэнтности (« »).

• Отношение подобия (« »).

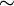• Отношение параллельности прямых (« »).

• Эквивалентность функций в математическом анализе:

Говорят, что функция   эквивалентна функции   при  , если она допускает представление вида  , где   при  . В этом случае пишут  , напоминая при необходимости, что речь идет о сравнении функций при  . Если   при  , эквивалентность функций   и   при  , очевидно, равносильна соотношению  .

• Отношение равномощности множеств.

№17 Отношения частичного порядка. Линейно- упорядоченные множества. Максим.(миним.) наимен(наибольш.) элементы частично упорядоченного множества и их свойства.

Частично упорядоченное множество — математическое понятие, которое формализует интуитивные идеи упорядочивания, расположения в определенной последовательности и т. п. Неформально говоря, множество частично упорядочено, если указано, какие элементы следуют (больше и т. п.) за какими. При этом в общем случае может оказаться так, что некоторые пары элементов не связаны отношением «следует за».

В качестве абстрактного примера можно привести совокупность подмножеств множества из трех элементов {x,y,z} (булеанданного множества), упорядоченное по отношению включения.

В качестве примера строгого частичного порядка «из жизни» можно привести множество людей, упорядоченное по отношению «быть предком».

Порядком, или частичным порядком, на множестве M называется бинарное отношение   на M (определяемое некоторым множеством  ), удовлетворяющее следующим условиям:

• Рефлексивность: 

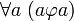
• Транзитивность: 

• Антисимметричность: 

Множество M, на котором задано отношение частичного порядка, называется частично упорядоченным (англ. partially ordered set, poset). Если быть совсем точным0^%A7^%D0^%B0^%D1^%81%D1^%82%D0^%B8^%D1^%87%D0^%BD%D0^%BE_%D1^%83%D0^%BF%D0^%BE%D1^%80%D1^%8^F%D0^%B4^%D0^%BE%D1^%87%D0^%B5^%D0^%BD%D0^%BD%D0^%BE%D0^%B5^_%D0^%BC%D0^%BD%D0^%BE%D0^%B6^%D0^%B5^%D1^%81%D1^%82%D0^%B2^%D0^%BE"[2], то частично упорядоченным множеством называется пара  , где M — множество, а   — отношение частичного порядка на M.

Отношение частичного порядка обычно обозначают символом  , по аналогии с отношением «меньше либо равно» на множестве действительных чисел. При этом, если  , то говорят, что элемент a не превосходит b, или что a подчинен b.

Если   и  , то пишут a < b, и говорят, что a меньше b, или что a строго подчинен b.

Иногда, чтобы отличить произвольный порядок на некотором множестве от известного отношения «меньше либо равно» на множестве действительных чисел, вместо   и <используют специальные символы   и   соответственно.

Отношение, удовлетворяющее условиям рефлексивности, транзитивности и антисимметричности, также называют нестрогим, или рефлексивным порядком. Если условие рефлексивности заменить на условие антирефлексивности:

то получим определение строгого, или антирефлексивного порядка.

Если   — нестрогий порядок на множестве M, то отношение < , определяемое как:

является строгим порядком на M. Обратно, если <  — строгий порядок, то отношение  , определенное как

является нестрогим порядком.

Поэтому все равно — задать на множестве нестрогий порядок, или строгий порядок. В результате получится одна и та же структура. Разница только в терминологии и обозначениях.

Из-за того, что в частично упорядоченном множестве могут быть пары несравнимых элементов, вводятся два различных определения: минимального элемента инаименьшего элемента.

Элемент   называется минимальным (англ. minimal element), если не существует элемента b < a. Другими словами, a — минимальный элемент, если для любого элемента   либо b > a, либо b = a, либо b и a несравнимы. Элемент a называется наименьшим (0%90%D0%BD%D0%B3%D0%BB%D0%B8%D0%B9%D1%81%D0%BA%D0%B8%D0%B9_%D1%8F%D0%B7%D1%8B%D0%BA"англ. least element, lower bound (opp. upper bound)), если для любого элемента   имеет место неравенство  . Очевидно, всякий наименьший элемент является также минимальным, но обратное в общем случае неверно: минимальный элемент a может и не быть наименьшим, если существуют элементы b, не сравнимые с a.

Очевидно, что если в множестве существует наименьший элемент, то он единственен. А вот минимальных элементов может быть несколько. В качестве примера рассмотрим множество   натуральных чисел без единицы, упорядоченное по отношению делимости  . Здесь минимальными элементами будут простые числа, а вот наименьшего элемента не существует.

№18 Цепи и антицепи, и их свойства.

Линейно упорядоченное множество или цепь ― частично упорядоченное множество, в котором для любых двух элементов a и b имеет место   или  .

Важнейший частный случай линейно упорядоченных множеств ― вполне упорядоченные множества.

Формулировка теоремы Дилуорса

Пусть n — наибольшее количество элементов антицепи (англ. antichain) данного конечного частично упорядоченного множества M. Тогда M можно разбить на n попарно непересекающихся цепей.

Другими словами, минимальное число непересекающихся цепей, которые в совокупности содержат все элементы частично упорядоченного множества M, равно максимально возможному числу элементов в подмножестве множества M, состоящем из попарно несравнимых элементов, если это число конечно.

№19 Булевы кубы и их характеристики. Расстояние между его элементами и их нумерация. Код Гроя.

В={0,1}

n-мерный булев куб — это множество Bⁿ (с заданным частичным порядком)

Совокупность всех булевых векторов размерности n называется булевым кубом размерностью Bⁿ.

Утверждение

Между множеством всех подмножеств множества U и булевым кубом Bⁿ, где n= =[U] можно установить взаимное соответствие, при котором операции объединения множества соответствует операции логического сложения (их характеристических векторов), операции пересечения множеств соответствует операция логического умножения их характеристических векторов, а операции дополнения – операция отрицания. Пустому множеству соответствует нулевой вектор, а универсальному – единичный.

Следствие

Множество всех характеристических векторов является булевой алгеброй.

- Вершины булева куба (именно так я понял, но х\з так ли это). И да, вершины куба можно занумеровать.

Булев куб размерности 1

Булев куб размерности 2

Булев куб размерности 3

В 3-мерном случае вершины куба имеют координаты: (0,0,0), (1,0,0), (0,1,0), (1,1,0), (0,0,1), (1,0,1), (0,1,1), (1,1,1) а вершины его грани построенной на первых дух ортах: (0,0,0), (1,0,0), (0,1,0), (1,1,0) Пусть размерность N=4. Вершины грани гиперкуба построенной на первых трех ортах будут иметь координаты (к координатам вершин куба добавится 0 в четвертой позиции): (0,0,0,0), (1,0,0,0), (0,1,0,0), (1,1,0,0), (0,0,1,0), (1,0,1,0), (0,1,1,0), (1,1,1,0)

Код Грея — система счисления, в которой два соседних значения различаются только в одном разряде. Наиболее часто на практике применяется рефлексный двоичный код Грея, хотя в общем случае существует бесконечное множество кодов Грея для систем счисления с любым основанием. В большинстве случаев, под термином «код Грея» понимают именно рефлексивный бинарный код Грея.

Изначально предназначался для защиты от ложного срабатывания электромеханических переключателей. Сегодня коды Грея широко используются для упрощения выявления и исправления ошибок в системах связи, а также в формировании сигналов обратной связи в системах управления.

Преобразование двоичного кода в код Грея

Коды Грея легко получаются из двоичных чисел путём побитовой операции «Исключающее ИЛИ» с тем же числом, сдвинутым вправо на один бит. Следовательно, i-й бит кода Грея G_i выражается через биты двоичного кода B_i следующим образом:

где – операция «исключающее ИЛИ»; биты нумеруются справа налево, начиная с младшего.

Преобразование кода Грея в двоичный код

Обратный алгоритм – преобразование кода Грея в двоичный код – можно выразить рекуррентной формулой

причём преобразование осуществляется побитно, начиная со старших разрядов, и значение B_{i + 1}, используемое в формуле, вычисляется на предыдущем шаге алгоритма. Действительно, если подставить в эту формулу вышеприведённое выражение для i-го бита кода Грея, получим

Однако приведённый алгоритм, связанный с манипуляцией отдельными битами, неудобен для программной реализации, поэтому на практике используют видоизменённый алгоритм:

где N – число битов в коде Грея (для увеличения быстродействия алгоритма в качестве N можно взять номер старшего ненулевого бита кода Грея); знак означает суммирование при помощи операции «исключающее ИЛИ», то есть

Действительно, подставив в формулу выражение для i-го бита кода Грея, получим

Здесь предполагается, что бит, выходящий за рамки разрядной сетки (B_{N + 1}), равен нулю.