Обработка плохо определенной информации

Природа неопределенности

1. Неопределенность в исходной информации

2. Неопределенность в знаниях

P_i = (C_i→R_i­,K_i)

C­_I – Посылка

R_i – Результат

K_i – Уверенность

3. Неопределенность постановки цели

F (x) – ext

x≤x^*

P_i = (C_i→R_i­,K_i) – Эксперт пишет правила

↓

Достоверно

K(C_i)

↓

Уверенность

K(R_i) = f (K(C_i), K_i)

Теоретико – вероятностный подход к обработке неопределенностей (плохо определенной информации)

P_i = (C_i→R_i­, K_i)

E_i→H_i

E_i – свидетельство

H_i – гипотеза

P_i (H_{i‌‌‌‌}‌‌‌‌ǀ E_i)

P = (E→H) P(HǀE)

Формула Байеса

P = (HǀE) = P (EǀH)

Модификация

Поделим

- шанс справедливости гипотезы H

- Условный шанс

– Модифицированная формула Байеса

– E-контр свидетельство

– E-свидетельство

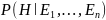, если свидетельства независимы

, i=1,n

, j=1,m

)

P =P(H) P (HǀE_i) = P(E_iǀH)

P_i⁺=P(E_i H) P(E_i) = P(E_i H)*P(H)+P(E_i H)*P(˥H)

P­_i^-= P(E_i H)

=

БЗ

– Априорная вероятность

– Свидетельство

– Номер свидетельства

Пример:

<Грипп, P, 2, {(1: 0,99; 0,01); (2: 0,9; 0,1)}>

1. Нет эпидемии

P=0,01

1. E₁(↑t)

P(HǀE₁)= =

2. E₂(Насморк)

P(HǀE₂)= =

3. E_1, E₂

P(Hǀ E_1,E₂)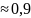

2. Эпидемия

P=0,1

1. P(HǀE₁)=0,9

2. P(HǀE₂)=0,5

3. P(Hǀ E_1,E₂)=1

Недостатки схемы Байеса

1. Неопределенность в свидетельствах

- Вводятся шкалы

0

1

-1

0

1

2. Независимость свидетельств

3. P(H) + P(˥H)=1

P(HǀE1,…,En) = 0,6

P(˥HǀE1,…,En) = 0,4

Трехзначная логика: {0; 0,5; 1}

Четырехзначная логика: {true, false, 0, τ}

Байесовские сети доверия

Пример

Схема

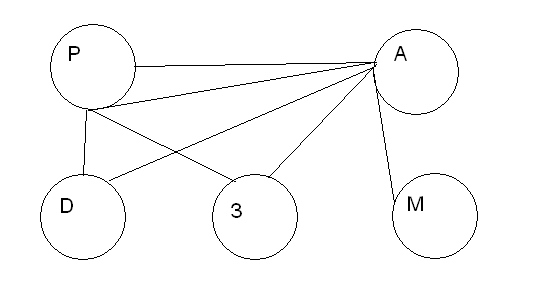
Р – ремонт дороги

А – авария

D – дорожные работы

З – Замедление

М – мигалка

Вероятность того, что Р при наличии З

P(RǀZ) = P(ZǀR)

=

R	Z	вероятность
True	True	0,3	0,75
True	False	0,2
False	True	0,1
False	False	0,4

P(R,A, D, 3, M) = P(R)*P(AǀR)*P(DǀR,A)*P(ZǀR,A,D)*P(MǀR,A,D,Z)

Сети:

• Родители не связаны

• У дочерней вершины не более двух родителей

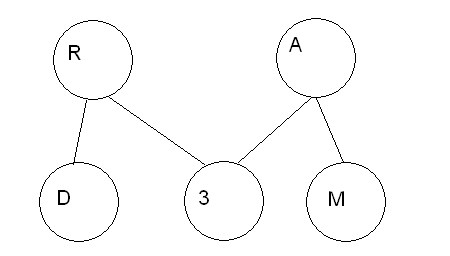
P(R,D,A,Z,M) = P(R)*P(A)*P(DǀR)*P(ZǀR,A)*P(MǀA)

Метод субъективных коэффициентов уверенности.

P(HǀE₁…E_n)=0,6

P(˥HǀE₁…E_n)=0,4

Мера доверия Мd(HǀE)

Мера недоверия Mn(HǀE)

M d(HǀE)= 1, если P(H) = 1

Max , если P(H) 1

M n(HǀE)= 1, если P(h)=0

, если P(H)

K(HǀE) = Md(HǀE)-Mn(HǀE) – коэффициент уверенности

0 Md, Mn 1

-1 K(HǀE) 1

K_{порог, н} K(HǀE)≤K_{порог в}

Если свидетельства сложные, то Ei и Ej независимы.

( 1)Md(HǀE_i&E_j) = 0, если Md(Hǀ E_i&E_j)=1

Mn(Hǀ E_i)+Mn(Hǀ E_j)- Mn(Hǀ E_i)*Mn(Hǀ E_j)

( 2)Mn(HǀE_i&E_j)= 0, если Md(HǀE_i&E_j)=1

Mn((HǀE_i)+Mn(HǀE_j)- Mn(HǀE_i)*Mn(HǀE_j)

Md(H_t&H_gǀE) = min

Mn(H_t&H_gǀE) = max

Md(H_t H_gǀE) = max

Mn(H_t H_gǀE) = min

Если свидетельства правдоподобные

Md(HǀA) = Md(HǀE)*max

Mn(HǀA) = Mn(HǀE)*max

Методы обработки плохо определенной информации в системе guru.

P_i = (C_i→R_i,K_i)

K(R_i) = f(K(C_i),K_i)

P_i = (C_i→R_i,K_i)

Pj = (C_j→R_j,K_j)

	AND(&) (E.CFJO)	OR (E.CFCO)
M	min
P	ab	A+b-ab
A
B	Ab(2- min	max + min

R-надежность поставщика

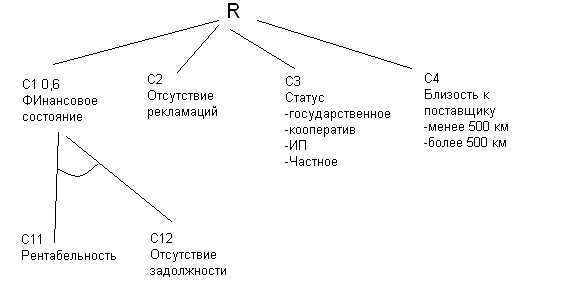
Правила:

P1=(C1→R; 0,9)

P2=(C2→R);0,8)

P32=(C3='кооператив'→R;0,5)

P32=(C3='ИП'→R;0,4)

P34=(C3='Частное'→R;0,4)

P31=(C3='Государственное'→R;0,6)

P4=(C4→R;0,6) или P4=(˥C4→R;0,3)

P11=(C11&C12→R1;1)

P12=(˥C11&C12→C1;0,6)

P13=(C11&˥C12→C1;0,8)

P14=(˥C11&˥C12→C1;1)

1. Нет неопределенности в исходных данных

(C11, c12, C2, C3=’кооператив’, C4)

MM: max 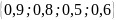=0,9

PP: 0,9+0,8-0,72=0,98

0,98+0,5-0,49=0,99

0,99+0,6-0,594=1

2. Если есть неопределенность в исходных данных

MM: =0,6

PP: 0,6*0,9+0,6*0,8-0,54*0,41=0,76

0,76+0,5-0,76*0,5=0,88

0,88+0,6-0,88*0,66=0,95

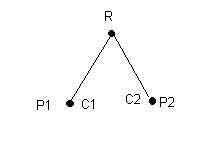
P1=(C1 →R,K1)

P2=(C2→R,K2)

K(R)=a+b-ab=0,9+0,8-0,72=0,98

K(R)=a(1-b)=0,9*0,2=0,18

4. 0,6 0,6

K(R)=0,6*0,9+0,6*0,8-0,54*0,48=0,76

0,6 -0,6

K(R)=0,6*0,9(1-0,8*0,6)=0,28

E.UNKN=n

0≤cf≤100

E.JCR=true