
- •Часть I
- •© Издательство ИжГту, 2008
- •Элементы векторной алгебры
- •II. Элементы линейной алгебры
- •Аналитическая геометрия
- •Введение в анализ
- •Дифференциальное исчисление функций одной переменной
- •Исследование функций и построение графиков
- •Комплексные числа
- •Интегральное исчисление функций одной переменной
- •Дифференциальное исчисление функций нескольких переменных
- •Элементы векторной алгебры
- •Элементы линейной алгебры
- •Аналитическая геометрия
- •Введение в анализ
- •Дифференциальное исчисление функций одной переменной
- •Исследование функций и построение графиков
- •Комплексные числа
- •Интегральное исчисление функций одной переменной
- •Дифференциальное исчисление функций нескольких переменных
- •Список литературы
- •Часть 1
Дифференциальное исчисление функций одной переменной
Найти производную функции у:
а) у = (1 + 4x2)3;
б) у = sin2x;
в) у = x arcsin(ln x) ;
г) у = x2 e−2x;
д)
у =
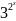 ;
;
е)
у = ln
(x
+
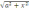
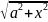 ;
;
ж)
у = xsinx ;
;
з) у = xlnx;
и)
y
=
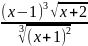
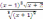 ;
;
к)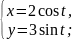
л)
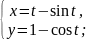
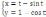
м)
x3
+ y3
=
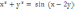 sin(x−2y);
sin(x−2y);
н) =1.
2. Установить правильное соответствие:
a)
|
1) |
б)
|
2)
|
в)
|
3)
– sin x; |
г)
|
4)
ex; |
д)
|
5)
|
е)
|
6) m xm-1; |
ж)
|
7)
cos x; |
з)
|
8)
|
и)
|
9)
− |
к)
|
10)
|
3. Выбрать правильный ответ.
Уравнение
касательной к параболе y2
=
4x
в точке M(1;2)
 имеет вид:
имеет вид:
а) y = − x + 3;
б) y = x + 1;
в) y = 2x + 1;
г) y = x +1.
4. Выбрать правильный ответ.
Уравнение нормали к кривой x2 + 2x y2 + 3y4 = 6 в точке В(1; −1) имеет вид:
а) 4x + y – 3 = 0;
б) x – 4y – 5 = 0;
в) 4x – y – 3 = 0;
г) –x – 4y – 5 = 0.
5. Найти дифференциал функции:
а) y = arctg x;
б)
y
= 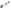
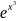 .
.
6. Вычислить приближенно, используя дифференциал:
a)
 ;
;
б)
 ln
1,02.
ln
1,02.
7. Найти дифференциал второго порядка для функций:
а)
y
=
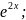

б)
y
= 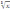
 .
.
8.
Найти точки, в которых касательная к
гиперболе y
=
 параллельна
прямой y
= −
параллельна
прямой y
= − 
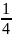 x
+ 3.
x
+ 3.
9. Вычислить с применением правила Лопиталя:
a)
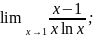
б)
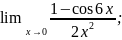
в)
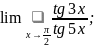
г)
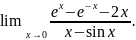
10. Найти производную n-го порядка функции y:
а) y = sin x;
б)
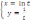
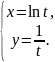
Исследование функций и построение графиков
1.Установить правильное соответствие:
а) четная функция; |
1) y = cos 8x; |
б) периодическая функция; |
2)
y = x2
+
5x; |
в)
|
3) y = x2 + 2sinx; |
г) функция не является ни четной, ни нечетной. |
4)
y = |
2.
Найти обратную функцию для y
=
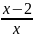 .
.
3. Какие из следующих функций являются монотонными:
а) y = c;
б) y = arctg x;
в) y = sin2 x;
г)
y
=
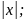
д)
y
= 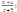
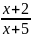 ;
;
ж)
y
=  –
x2
+ 2x.
–
x2
+ 2x.
4. Выбрать правильный ответ.
Вертикальная
асимптота графика функции у = 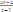
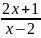 :
:
а) x = 2;
б) y = 2;
в)
x
= −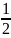
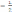 ;
;
г) x = – 2.
5. Выбрать правильный ответ.
Наклонная
асимптота графика функции у = 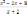
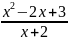 :
:
а) y = x + 2;
б) x = – 2;
в) y = x + 4;
г) y = x – 4.
6.
В каких из перечисленных точек функция
у =
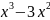 возрастает:
возрастает:
а) x = 3;
б) x = 1;
в) x = – 1;
г) x = 0,5.
7. Найти точки перегиба функции y = (x + 1)2(x − 2).
8. Исследовать на экстремум функцию y = (x – 5)ex.
9. Найти наибольшее и наименьшее значения функции y = 3x – x2 на отрезке [−2;3].
10.
Функция f(x)
=
представлена в виде многочлена пятой
степени относительно
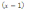 двучлена x
– 1:
двучлена x
– 1:
=
1+
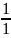 (x
– 1) −
(x
– 1) −
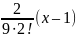 2
+
2
+
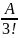 (x
– 1)3
−
(x
– 1)3
−
 (x
– 1)4
+
(x
– 1)4
+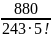 (x
– 1)5+
R5,
(x
– 1)5+
R5,
где
R5
=
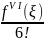 (x
– 1)6,
1 < ξ
< x.
Найти А.
(x
– 1)6,
1 < ξ
< x.
Найти А.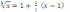

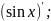
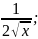
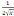
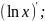
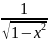 ;
;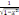
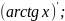
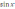



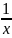 ;
;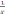
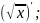

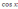
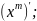
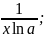
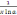

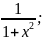
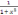

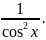

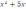
 нечетная
функция;
нечетная
функция;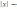
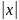 −
5
−
5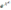
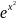 .
.