
- •Часть I
- •© Издательство ИжГту, 2008
- •Элементы векторной алгебры
- •II. Элементы линейной алгебры
- •Аналитическая геометрия
- •Введение в анализ
- •Дифференциальное исчисление функций одной переменной
- •Исследование функций и построение графиков
- •Комплексные числа
- •Интегральное исчисление функций одной переменной
- •Дифференциальное исчисление функций нескольких переменных
- •Элементы векторной алгебры
- •Элементы линейной алгебры
- •Аналитическая геометрия
- •Введение в анализ
- •Дифференциальное исчисление функций одной переменной
- •Исследование функций и построение графиков
- •Комплексные числа
- •Интегральное исчисление функций одной переменной
- •Дифференциальное исчисление функций нескольких переменных
- •Список литературы
- •Часть 1
Аналитическая геометрия
1. Установить правильное соответствие:
а) y2 = 8x; |
1) гипербола; |
б)
x2+
y2
|
2) прямая; |
в) x – y + 3 = 0; |
3) парабола; |
г) x2 – y2 =8. |
4) эллипс. |
2. Установить взаимное расположение прямых:
а) 3x + 5y – 9 = 0 и 10x − 6y + 4 = 0;
б) 2x + 5y – 2 = 0 и x + y + 4 = 0;
в) 2x + 3y = 8 и x+ y − 3 = 0;
г)
2/3 x
–
3/4
 y
−1 = 0 и
3/4
x
+
2/3y
+ 2 = 0;
y
−1 = 0 и
3/4
x
+
2/3y
+ 2 = 0;
д) x + 8 = 0 и 2x – 3 = 0.
3.
Найти направляющий вектор прямой


4. Указать вид уравнений прямой:
а)
б)
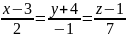
 ;
;
в)

г) y = 3x +2;
д)

 = 0;
= 0;
е)
 =
1.
=
1.
5. Найти площадь квадрата, если две его стороны лежат на прямых
5x – 12y – 65 = 0 и 5x – 12y + 26 = 0.
6. Найти нормальный вектор плоскости 4x + 2y – 11z + 18 = 0.
7. Плоскость задана тремя точками А (1; 0; −1), В (2; 2; 3), С (0; −3; 1). Записать ее уравнение.
8. Записать уравнение прямой, проходящей через точку М (0; −2; 0) перпендикулярно плоскости 2х − 3у + z + 6 = 0.
9. Найти расстояние от прямой 2x + y – 5 = 0 до начала координат.
10. На каком расстоянии от плоскости x + 2y – 2z − 9 = 0 находится точка М(3; 5; −2)?
11. Какая поверхность задана уравнением:
а)

 = z;
= z;
б)
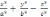
 +
+
 =1;
=1;
в)
+
 =1;
=1;
г)
 +
+
 =1;
=1;
д)

 = z;
= z;
е)
y2 = 2px;
= 2px;
ж) + = 1.
12. Установить, какие линии определяются следующими уравнениями:
а)
x
= 
 ;
;
б)
y
=
3

 ;
;
в)
y
=
2
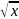 ;
;
г)
x
=


13. Составить уравнение параболы, вершина которой находится в начале координат. Парабола симметрична относительно оси ОХ и проходит через точку А (9; 6).
14. Найти полуоси, фокусы и эксцентриситет:
а)
гиперболы 16

 =
144;
=
144;
б)
эллипса 9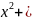
 25
25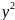 = 225.
= 225.
15. Определить, какие линии даны следующими уравнениями в полярных координатах:
а)
ρ =
 ;
;
б)
ρ =
 ;
;
в)
ρ =
 ;
;
г)
ρ =
 .
.
Введение в анализ
1. Установить правильное соответствие:
а)
|
1) ограниченная последовательность; |
б)
|
2) неограниченная последовательность; |
в) 1,2,3,4,…; |
3) бесконечно малая; |
г) 2, 4, 8, 16, … . |
4) бесконечно большая. |
2. Найти область определения функции:
а)
y
= 
 + 1;
+ 1;
б)
y = arccos

 ;
;
в)
y = 
 ;
;
г)
y
=
lg
(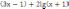 3x−1)
+ 2lg
(x+1).
3x−1)
+ 2lg
(x+1).
3. Вычислить пределы:
a)
|
д)
|
б)
|
е)
|
в)
|
ж)
|
г)
|
з)
|
4.
Выбрать
все
верные утверждения.
Для функции y
= arctg
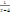
 :
:
а) точка x = 4 является точкой разрыва I рода;
б) точка x = 4 является точкой разрыва II рода;
в) скачок функции в точке х = 4 равен π;
г) в точке х = 4 функция непрерывна.
5. Найти точки разрыва функций:
а)
у =

 ;
;
б)
y
= 
 ;
;
в)
y
=

6. Выбрать правильный ответ.
Функция
y
= 
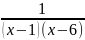 непрерывна на промежутке:
непрерывна на промежутке:
а)
(2;5) ;
;
б)
(4;10) ;
;
в)
(0;7);
г)
(−
 .
.
7. Установить правильное соответствие.
Бесконечно малые эквивалентны (при α→ 0, β→∞):
а) sin α; |
1) α ; |
б) tg α; |
2)
|
в)
|
3)
|
г)
|
4)
|
д) 1− cos α; |
5)
|
е)
|
6)
α |
ж)
|
|
з) arcsin α; |
|
и)
|
|
к) arctg α. |
|
л)
|
|
8. Вычислить:
a)
|
б)
|
в)
|
г)
|

 +
8x
− 4y + 29 = 0;
+
8x
− 4y + 29 = 0;











 ;
;
 − 1;
− 1;

 ;
;
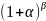 ;
;
 ;
;
 ;
;
 .
.
 ;
;
 −1;
−1; .
.


