15. Устойчивость су. Обзор методов ее анализа. Критерии устойчивости су.

Понятие устойчивости системы связано со способностью системы возвращаться в состояние равновесия после исчезновения внешних сил, которые вывели ее из этого состояния. Если система неустойчива, то она не возвращается в состояние равновесия.

При возмущениях в системе возникают колебания Y(t), которые могут быть затухающими, незатухающими, стремящимися к положению равновесия, или уходящими от него (неустойчивые).

Систему называют устойчивой, если будучи выведенной из состояния равновесия она возвращается (с допустимой погрешностью) к прежнему положению после снятия возмущающего воздействия. Простейшая аналогия устойчивости – шарик внутри вогнутой поверхности, который всегда возвращается в самое нижнее положение на поверхности независимо от того, выведен ли он из этого положения движением самой поверхности или импульсным воздействием на шарик. Шарик на выпуклой поверхности – пример неустойчивой системы.

При определении устойчивости системы рассматривается ее свободное поведение при равенстве нулю возмущающих входных воздействий. Состояние системы определяется однородным дифференциальным уравнением замкнутой системы: a_n y⁽ⁿ⁾ + a_n-1 y^(n-1) + … +a₁ y' + a₀ = 0.

Характеристическое уравнение: a_n p⁽ⁿ⁾ + a_n-1 p^(n-1) + … +a₁ p' + a₀ = 0.

Общее решение: Y(t) = C_k exp(p_kt), если p_k – действительные корни.

Положение А.М. Ляпунова для определения устойчивости систем по корням характеристического уравнения:

1. Если характеристическое уравнение линеаризованной системы имеет все корни с отрицательными действительными числами, то система устойчива.

2. Если хотя бы один корень имеет положительную часть, то система неустойчива.

3. При наличии нулевых или чисто мнимых корней поведение реальной системы не всегда (даже качественно) определяется её линеаризованным уравнением.

Методы анализа:

1.Теорема Ляпунова (об устойчивости по первому приближению).

Рассмотрим систему дифференциальных уравнений Решение , системы асимптотически устойчиво, если все собственные значения матрицы , имеют отрицательные действительные части, если же хоть одно собственное значение имеет положительную вещественную часть, то нулевое решение неустойчиво.

2.Критерий Рауса-Гурвица

Рассмотрим условия отрицательности всех действительных частей корней уравнения с действительными коэффициентами.

Необходимым условием отрицательности всех действительных частей корней уравнения являются неравенства , . Матрица вида

п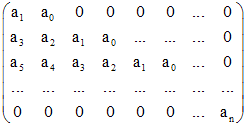 олучаемая заменой чисел с индексами или нулями, называется матрицей Гурвица.

Критерий Рауса -Гурвица

Для отрицательности всех действительных частей корней уравнения

необходимо и достаточно, чтобы были положительными все главные диагональные миноры матрицы Гурвица:

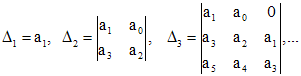
3.Критерий Найквиста

Критерий Найквиста предназначен для исследования только замкнутых систем. Он позволяет по виду амплитудно-фазовой частотной характеристики разомкнутой системы судить об устойчивости замкнутой системы.

Пусть l корней характеристического уравнения разомкнутой системы находятся в правой полуплоскости, а остальные (n – l) корней - в левой полуплоскости. Тогда, для того чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы амплитудно-фазовая частотная характеристика ее разомкнутой системы с ростом от 0 до охватывала точку (-1, j0) в положительном направлении, т. е. против движения часовой стрелки, l/2 раз.

В частности, если разомкнутая система устойчива (и, следовательно, l = 0), то, для того чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы амплитудно-фазовая частотная характеристика ее разомкнутой системы не охватывала точку (-1, j0).