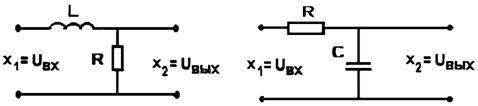- •1.Виды систем автоматического управления.
- •По цели управления:
- •1)Системы автоматического регулирования
- •2)Системы экстремального регулирования
- •3)Адаптивные системы автоматического управления По виду информации в управляющем устройстве Замкнутые сау
- •Разомкнутые сау
- •2.Основные определения, функциональные схемы и задачи автоматического управления (основы управления).
- •Основные понятия
- •Функциональные схемы
- •Понятие качества управления.
- •Функциональная схема су.
- •5. История развития теории управления.
- •История
- •6. Классификация су по виду используемой информации в управлении.
- •Замкнутые сау
- •Разомкнутые сау
- •7. Классификация су по виду задающего воздействия и количеству регулируемых координат на объекте.
- •8. Классификация су по математическому описанию и принципу действия сау во времени.
- •11. Типовые звенья су. Безинерционные звенья
- •Безынерционное (пропорциональное, усилительное) звено
- •12. Типовые звенья су. Инерционные звенья 1 и 2-го порядков.
- •Инерционное звено первого порядка (апериодическое)
- •Инерционные звенья второго порядка
- •13. Типовые звенья су. Интегрирующие и дифференцирующие звенья.
- •Интегрирующее (астатическое) звено
- •Дифференцирующее звено
- •14. Типовые звенья су. Форсирующие звенья.
- •Устойчивость су. Обзор методов ее анализа. Критерии устойчивости су.
- •Методы анализа:
- •2.Критерий Рауса-Гурвица
- •3.Критерий Найквиста
- •Критерии устойчивости:
- •16.Корневой метод для анализа устойчивости су.
- •3. Второй (прямой) метод Ляпунова
- •4. Теоремы Ляпунова об устойчивости нелинейных систем
- •17. Критерий Рауса-Гурвица для анализа устойчивости су.
- •Формулировка
- •К вопросу об автоматизации метода
- •18. Критерий устойчивости Михайлова
- •21. Частотные характеристики типовых звеньев сау. Безынерционные звенья.
- •Частотные характеристики типовых звеньев сау. Инерционные звенья 1 и 2-го порядков. Инерционное (апериодическое) звено первого порядка
- •23. Частотные характеристики типовых звеньев сау. Интегрирующее и дифференцирующее звенья.
- •Частотные характеристики типовых звеньев сау. Звено чистого запаздывания.
- •25. Виды динамических систем и свойства объектов управления.
- •26. Особенности математического описания сигналов и типовые воздействия.
- •29. Запасы устойчивости су.
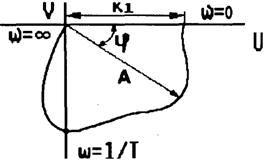
- •Области устойчивости су. Метод корневого годографа.
- •31. Области устойчивости су. Метод Вышнеградского.
- •Области устойчивости су. Метод d-разбиения плоскости одного параметра.
- •Области устойчивости су. Метод d-разбиения плоскости двух параметров.
- •34. Статические режимы су.
- •35 Установившийся статический режим. Статика су
- •36. Способы повышения точности су
- •37. Структурная устойчивость су.
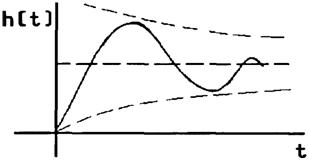
- •Качество переходных процессов в линейных сау.
- •Коррекция динамических свойств линейных сау.
- •40. Нелинейные сау
- •Классификация
- •Задачи исследования:
- •Особенности динамики нелинейных систем
18. Критерий устойчивости Михайлова
Критерий Михайлова сформулирован и обоснован в 1936 году русским ученым А.В. Михайловым.
Критерий Михайлова позволяет оценивать устойчивость как замкнутых, так и разомкнутых систем.
Частотные критерии устойчивости получили наиболее широкое практическое применение, так как, во-первых, они позволяют судить об устойчивости замкнутой системы по более простой передаточной функции системы W ( s ) ; во-вторых, анализ устойчивости можно выполнять и по экспериментально определенным частотным характеристикам; в-третьих, с помощью частотных характеристик можно судить и о качестве переходных процессов в системе.
Критерий Михайлова формулируется так:
система устойчива, если годограф Михайлова M(jω) при изменении от 0 до + беск. , начинаясь на положительной части действительной оси, обходил последовательно в положительном направлении (против часовой стрелки) n квадрантов и в n-м квадранте уходил в беск. .
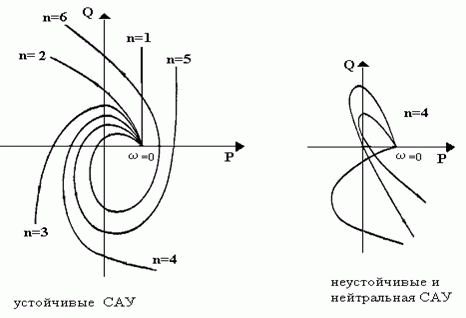
Имеется вторая формулировка критерия Михайлова: для устойчивости системы необходимо и достаточно, чтобы корни уравнений P(ω) = 0 и Q(ω) = 0 перемежались (чередовались), т.е. годограф последовательно пересекал оси комплексной плоскости. Этой формулировкой удобно пользоваться для исследования устойчивости систем до пятого порядка включительно.
Практическая формулировка критерия Михайлова. Система будет устойчива, если при возрастании w от 0 до , годограф, начинаясь на положительной части вещественной оси, проходит последовательно в положительном направлении n квадрантов, где n - степень характеристического уравнения.
Критерий Михайлова является частотным критерием устойчивости.
В его основу положен принцип аргумента, известный из теории функций комплексного переменного.
21. Частотные характеристики типовых звеньев сау. Безынерционные звенья.
Усилительное звено (безынерционное, пропорциональное). Усилительным называют звено, которое описывается уравнением:
![]() (2)
(2)
или передаточной функцией:
![]() (3)
(3)
При этом переходная функция усилительного звена (рис. 1а) и его фун-кция веса (рис. 1б) соответственно имеют вид:
![]()
![]()

а) б)
Рис. 1
Частотные характеристики звена (рис. 2) можно получить по его передаточной функции, при этом АФХ, АЧХ и ФЧХ определяются следующими соотношениями:
![]() .
.

h(t)




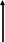
Рис. 2
Л огарифмическая
частотная характеристика усилительного
звена (рис. 3) определяются соотношением
огарифмическая
частотная характеристика усилительного
звена (рис. 3) определяются соотношением
![]() .
.
Частотные характеристики типовых звеньев сау. Инерционные звенья 1 и 2-го порядков. Инерционное (апериодическое) звено первого порядка
Уравнение и передаточная функция звена
![]() .
.
Частотная передаточная функция (АФХ)
![]() .
.
Умножив числитель и знаменатель на комплексно-сопряженную знаменателю функцию, получим
![]()
Вещественная частотная ВЧХ U(w) и мнимая V(w) МЧХ частотная характеристики:
![]() ,
,
![]() .
.
Амплитудная АЧХ и фазовая ФЧХ частотные характеристики (рис.2.16,б):
![]() (2.36)
(2.36)
![]() (2.37)
(2.37)
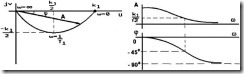
АФХ
(рис.2.16,а) представляет собой полуокружность
для частот
![]() .
Действительно,
.
Действительно,
![]() .
.
Сравнивая
выражения U(w)
и A(w),
видим, что
![]() Тогда
Тогда
![]()
 .
.
представляет собой уравнение окружности при изменении частоты -¥ £ w £ +¥.
Радиус
этой окружности
![]() ,
центр ее располагается по положительной
оси U(w)
на удалении
,
центр ее располагается по положительной
оси U(w)
на удалении
![]() .
.
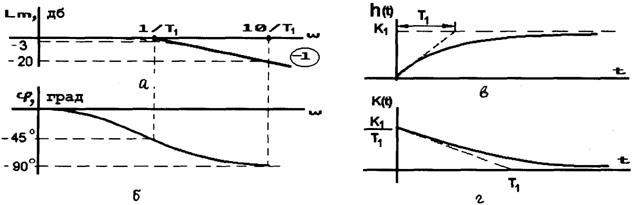
а б Рис. 2.16. Логарифмическая амплитудная частотная характеристика (рис.2.17,а) |
![]() .
.
Для построения ЛАХ примем К1= 1 и рассмотрим три участка ЛАХ:
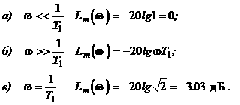
В
области высоких частот при
![]() ЛАХ
является линейной функцией логарифма
частоты и обращается в нуль, т.е.
сопрягается с выражением Lm(w)
в области низких частот при частоте
ЛАХ
является линейной функцией логарифма
частоты и обращается в нуль, т.е.
сопрягается с выражением Lm(w)
в области низких частот при частоте
![]() ,
называемой сопрягающей частотой. Если
увеличить частоту w в 10 раз,
,
называемой сопрягающей частотой. Если
увеличить частоту w в 10 раз,
![]() ,
то получим
,
то получим
![]()
Таким образом, в области высоких частот ЛАХ апериодического звена представляется прямой линией с наклоном -20дБ/дек.
В дальнейшем наклоны ± 20дБ/дек, ± 40дБ/дек будем обозначать соответственно ±1, ±2.
Наибольшее
отличие асимптотической ЛАХ от точной
будет на частоте сопряжения
![]() ,
равно -3 дБ.
,
равно -3 дБ.
Если
коэффициент К1
апериодического звена не равен 1 (
![]() ),
то при
),
то при
![]() ЛАХ
смещается параллельно вверх на величину
20 lg
ЛАХ
смещается параллельно вверх на величину
20 lg![]() ,
а при
,
а при
![]() -
вниз вдоль оси ординат на
-
вниз вдоль оси ординат на
![]() .
.
Рис. 2.17 |
Переходная
функция, согласно решению уравнения
звена, при
![]() и
нулевых начальных условиях представляет
собой экспоненту (рис.2.17.в) и описывается
выражением
и
нулевых начальных условиях представляет
собой экспоненту (рис.2.17.в) и описывается
выражением
![]() .
.
Импульсно-переходная (весовая) функция (рис.2.1.г)
![]() .
.
Примером
апериодического звена могут быть:
электродвигатель постоянного тока (в
первом приближении), если
![]() -
управляющее напряжение,
-
управляющее напряжение,![]() - угловая скорость вала двигателя;
сглаживающие L-R и R-С - фильтры (рис.2.18).
- угловая скорость вала двигателя;
сглаживающие L-R и R-С - фильтры (рис.2.18).
Рис. 2.18 |
Инерционное звено второго порядка
Вид дифференциального уравнения
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Передаточная функция
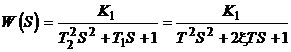 .
.
При
выполнении условия![]()
корни характеристического уравнения
![]() ,
,
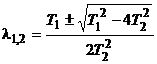 будут
вещественными.
будут
вещественными.
В этом случае инерционное звено 2-го порядка называют апериодическим звеном 2-го порядка. Его передаточная функция
![]() ,
,
![]()
Рис. 2.19, а |
Переходная характеристика (рис.2.19,а)
![]()
где
![]()
АФЧХ (рис.2.19,б)
![]()
АЧХ
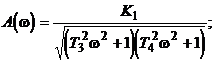
ФЧХ (рис.2.20)
![]()
ЛАХ (рис.2.20)
![]()
Рис. 2.19, б Рис. 2.20 |
Если
![]() ,
то
частоты сопряжения сходятся в одну
точку.
,
то
частоты сопряжения сходятся в одну
точку.
Примером такого звена является двигатель постоянного тока при учете инерционности цепи якоря, электромашинный усилитель.
Если
выполняется условие
![]() ,
то корни характеристического
,
то корни характеристического
уравнения
![]() -
комплексные.
-
комплексные.
Инерционное звено 2-го порядка с передаточной функцией
![]()
называется колебательным;
![]() -
параметр затухания (коэффициент
относительного демпфирования).
-
параметр затухания (коэффициент
относительного демпфирования).
Переходная характеристика (рис.2.21)
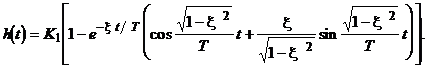
Рис. 2.21 |
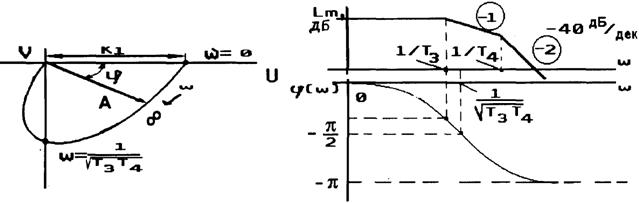
Амплитудно-фазовая характеристика (рис.2.22);
![]()
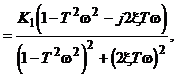 (2.39)
(2.39)
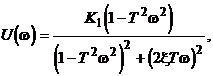
Рис. 2.22 |
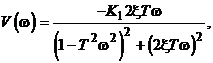
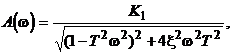 (2.40)
(2.40)
![]()
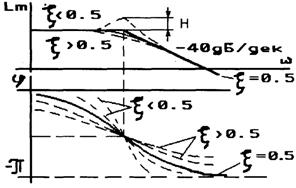
ЛАХ и ФЧХ (рис.2.23):
![]() (2.41)
(2.41)
1)
![]()
![]()
Рис. 2.23 |
![]()
2)
![]()
![]()
Пусть
![]() ,
,
![]() ,
следовательно
,
следовательно
![]() а
а
![]()
При
![]()
При
![]()
3)![]()
Таким
образом, асимптотическая ЛАЧХ в области
низких частот
![]() параллельна
оси частот, а при
параллельна
оси частот, а при
![]() имеет
наклон "-2", т.е. -40 дБ/дек.
имеет
наклон "-2", т.е. -40 дБ/дек.
При
значениях
![]() характеристика
близка к ломаной. Если же
характеристика
близка к ломаной. Если же
![]() ,
то получится заметный горб (резонансный
пик). Имеются шаблоны для вычерчивания
точной ЛАХ. В упрощенных расчетах
достаточно находить величину резонансного
пика на частоте сопряжения:
,
то получится заметный горб (резонансный
пик). Имеются шаблоны для вычерчивания
точной ЛАХ. В упрощенных расчетах
достаточно находить величину резонансного
пика на частоте сопряжения:
![]()