Глава 4. Устойчивость сау

Продолжим изучение САУ, которые описываются линейными дифференциальными уравнениями с постоянными вещественными коэффициентами

.

Можно показать, что решение уравнения представляется в виде:

, где  любое частное решение , определяемое входным сигналом u(t), а  общее решение соответствующего однородного уравнения.

Частные решения , когда входными сигналами были единичная функция 1(t), дельта-функция (t) и периодическое возмущение e^{i t} изучены во второй и третьей главах. Теперь изучим поведение общего решения однородного уравнения .

Характеристический полином, соответствующий однородному уравнению , имеет вид

P_n() = a_n  ⁿ + ... + a₁  + a₀ .

Характеристический полином называется устойчивым или гурвицевым, если все его корни находятся в левой полуплоскости. Соответственно САУ, для которой характеристический полином устойчив, называется устойчивой САУ. Отметим, что для устойчивой САУ  0 при t   , поскольку в решении однородного уравнения присутствуют экспоненты с отрицательными показателями. При этом .

Если существует: то x_ называется установившимся режимом САУ. Для устойчивой САУ, у которой частное решение не зависит от времени, установившимся режимом будет это частное решение x_ = .

1. Алгебраический критерий устойчивости Гурвица.

Область устойчивости в пространстве параметров

Сформулируем необходимые и достаточные условия того, что характеристический полином устойчив. Введем обозначения a_k= a_{n - k} (k = 0,1, ...,n) и перепишем характеристический полином в виде

P_n() = a₀  ⁿ + ... + a_n-1  + a_n .

По коэффициентам a_k характеристического полинома составим квадратную матрицу H размером (nn) , которая называется матрицей Гурвица

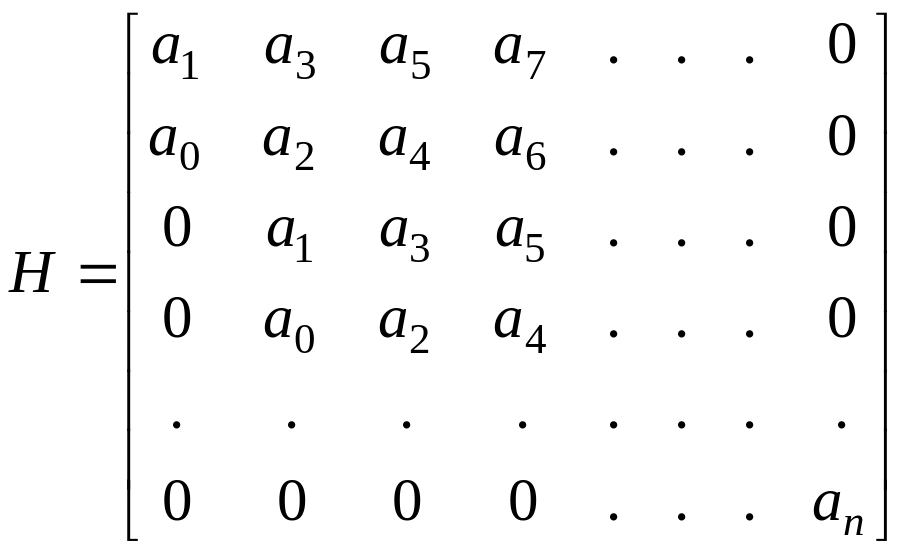
В первой строке матрицы H расположены в порядке возрастания нечетных индексов коэффициенты a, начиная с a₁; во второй строке  в порядке возрастания четных индексов, начиная с a₀. По главной диагонали расположены коэффициенты a₁ , ... , a_n . После a_n коэффициенты заменяются нулями.

Выпишем главные диагональные миноры матрицы Гурвица

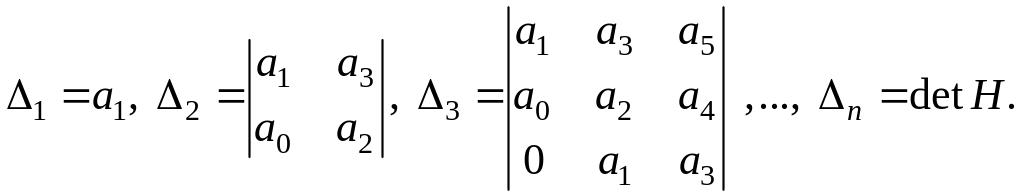
Критерий Гурвица. Для того, чтобы характеристический полином , у которого a₀ > 0 , был устойчив, необходимо и достаточно, чтобы все диагональные миноры матрицы Гурвица были строго положительны

_k > 0 (k = 1,...,n) .

Необходимый критерий устойчивости. Положительность всех коэффициентов характеристического полинома  необходимое условие его устойчивости. Заметим, что для полиномов первого и второго порядков необходимое условие устойчивости является и достаточным.

Выпишем, согласно [1], условия устойчивости для полиномов третьего и четвертого порядков (считаем, что все a_i > 0 ):

n =3, a₁ a₂ - a₀ a₃ > 0 ;

n =4, a₃ (a₁ a₂ - a₀ a₃) - a₄ a₁² > 0 .

Предположим, что коэффициенты a_i характеристического полинома зависят от параметров в этом случае неравенства задают в пространстве параметров область устойчивости . При выборе точки внутри области САУ будет устойчивой.

Задание для самоконтроля. построить область устойчивости для САУ на Рис. 1.7 в качестве параметров выбрать коэффициент усиления и постоянную времени второго блока: .