4.3.1. Критерий асимптотической устойчивости замкнутой системы, содержащей лишь устойчивые звенья

Пусть САУ состоит из устойчивых звеньев, а характеристическое уравнение разомкнутой системы не имеет нулей в правой полуплоскости. В этом случае и формула принимает вид

Таким образом, САУ устойчива, если число оборотов АФЧХ разомкнутой системы вокруг точки (-1,0) равно нулю.

В частном случае, когда контур Г не имеет самопересечений, справедлив следующий критерий.

Критерий Найквиста. САУ асимптотически устойчива, если точка (-1,0) лежит вне контура Г.

Заметим, что контур Г может охватывать точку (-1,0), но наличие самопересечений этого контура делает САУ устойчивой.

Расположение точек f(0),f(∞)на оси абсцисс

Пусть разомкнутая и замкнутая САУ устойчивы. При этом пары чисел и должны иметь одинаковые знаки. В противном случае полиномы будут иметь положительный корень на интервале , что противоречит предположению об устойчивости разомкнутой и замкнутой САУ. Так как , то числа также имеют одинаковые знаки, значит точки лежат по одну сторону от точки (-1,0).

Вывод. Если точки лежат по разные стороны от точки (-1,0), то замкнутая САУ неустойчива. Если же эти точки лежат по одну сторону, то замкнутая САУ может быть либо устойчивой, либо неустойчивой.

4.3.2. Применение критерия Найквиста к системам с нейтральными звеньями

Пусть передаточная функция разомкнутой САУ содержит одно интегрирующее звено 1/p. Звенья, для которых характеристические полиномы содержат корни на мнимой оси называются нейтральными.

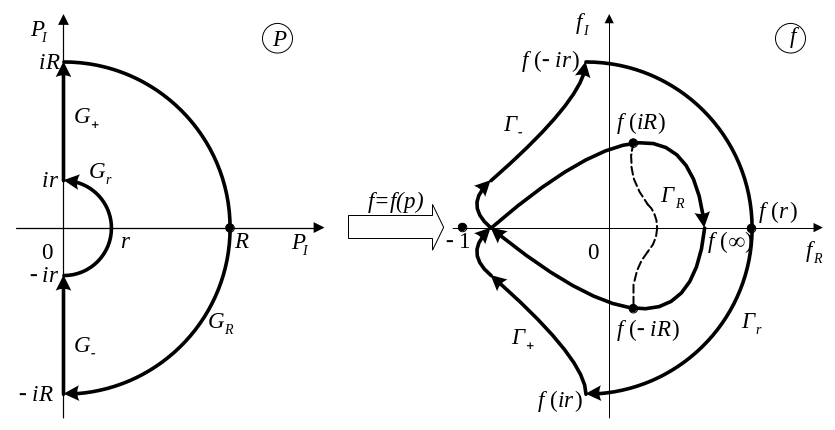
Рис 4.5 Кривая Найквиста для системы с нейтральным звеном 1/p

В плоскости p выберем контур (Рис. 4.5 слева). При этом с помощью полуокружности малого радиуса r Исключим полюс 1/p передаточной функции .

В пределе при контур G охватывает всю правую полуплоскость. Вблизи функция ведет себя, как , где . При этом бесконечные ветви кривой должны быть замкнуты полуокружностью бесконечно большого радиуса, пробегаемую по стрелке часов (рис. 4.5 справа).

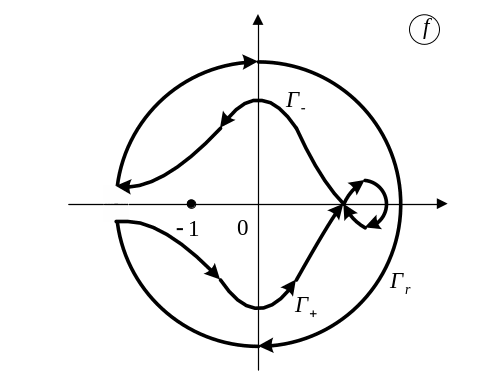
Рис 4.6 Кривая Найквиста для системы с нейтральным звеном

На рис. 4.6 представлен годограф Найквиста для функции , у которой в нуле имеется полюс второго порядка, т.е. САУ содержит звено . В этом случае ветви кривой должны быть замкнуты двумя полуокружностями бесконечно большого радиуса.

В общем случае, когда САУ содержит нейтральные звенья, характеристические полиномы которых имеют l корней (с учетом их кратности) на мнимой оси, формула принимает вид.

,

где число поворотов по часовой стрелке контура вокруг точки (-1,0).

4.3.3 Применение критерия Найквиста к системам с неустойчивыми звеньями

Рассмотрим САУ, которая содержит неустойчивые звенья. При этом характеристический полином разомкнутой системы будет содержать нули в правой полуплоскости. Для определенности предположим что уравнение имеет корень кратности l на оси абсцисс, т.е. передаточная функция разомкнутой САУ имеет полюс

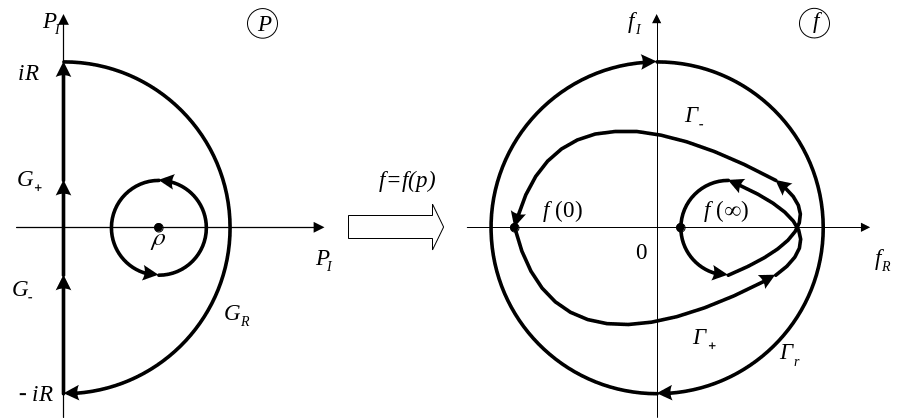
Рис 4.7 Кривая Найквиста для САУ с неустойчивым звеном

В плоскости (рис. 4.7 слева). При этом с помощью полуокружности радиусом и центром на оси абсцисс передаточной функции (окружность пробегается по стрелке часов).

В пределе при контур охватывает всю правую полуплоскость. Вблизи функция ведет себя, как

,

где . При этом на плоскости к контуру добавляется окружность бесконечно большого радиуса, пробегаемая по стрелке часов раз (рис. 4.7 справа).

В общем случае, когда САУ содержит неустойчивые звенья, характеристические полиномы которых имеют корней (с учетом кратности) в правой полуплоскости, формула принимает вид

,

где - число поворотов по часовой стрелке контура вокруг точки (-1,0).

Замечание. Если полином имеет корней (с учетом кратности) на мнимой оси и корней с учетом кратности) в правой полуплоскости, то .