1 3. Стандартные виды аксонометрических проекций. Коэффициенты искажения. Построение окружности в аксонометрических проекциях.

ГОСТ 2.317–69 рекомендует использовать следующие аксонометрические проекции: прямоугольная изометрическая проекция; прямоугольная диметрическая проекция; косоугольная фронтальная диметрическая проекция; косоугольная фронтальная изометрическая проекция; косоугольная горизонтальная изометрическая проекция.

Прямоугольная изометрическая проекция.

Аксонометрические оси в изометрии размещены под углом 120° одна от другой, причем ось Z размещается всегда вертикально. Коэффициенты искажения по всех осях равны между собой: k=m=n, k²+m²+n²=3k²=2  k=0,82. Для упрощения построения принимают коэффициенты искажения равными единицы. В этом случае аксонометрическая проекция получается увеличенной в 1,22 раза относительно натуральной величины предмета. Окружность, размещенная в координатных плоскостях или плоскостях, которые им параллельны, проецируются в виде эллипсов. Большая полуось АВ размещается перпендикулярно к той сои, которой нет в плоскости размещения окружности. Размеры осей эллипсов: большая полуось — АВ=1,22d; малая ось — CD=0,7d, где d — диаметр проецируемой окружности.

Прямоугольная диметрическая проекция.

В прямоугольной диметрической проекции ось Х размещается под углом 7°10´ к горизонтальной линии, ось Y под углом 41º25´ к этой же линии. Ось Z — вертикально. Коэффициенты искажения по осях Х и Z равны между собой, а по оси Y=0,5, k=n; m=½k. Тогда равенство k²+m²+n²=2k²+¼k²=2  k=0,94. Для построения принимают коэффициенты искажения по осях X и Z=1, по оси Y=0,5. Построены чертеж при этом получается увеличенным в 1,06 раз. Окружности, находящиеся в координатных плоскостях, как и в изометрии, проецируются в виде эллипсов. В плоскостях ХОY и ZOY или им параллельных эллипсы по форме и размерах одинаковы. Большая ось АВ=1,06d, малая ось CD=0,35d. В плоскости ХОY большая ось АВ=1,06d, малая ось CD=0,35d (d — диаметр окружности). Большая ось размещается перпендикулярно к отсутствующей оси плоскости размещения окружности.

Косоугольные аксонометрические проекции.

Часто применяется такая косоугольная диметрия, коэффициенты искажения которой по оси Y принимаются равными 0,5, а угол между этой осью и другими осями равен 135°. Такая аксонометрия называется фронтальной диметрической проекцией. Особенностью данной проекции является то, что окружность проецируется без искажения на фронтальную плоскость проекций.

1 4. Способы преобразования проекций. Способ плоскопараллельного перемещения.

Способы преобразования проекций: перемена плоскостей проекций; вращение вокруг проецирующей прямой; вращение вокруг линий уровня; плоскопараллельное перемещение; совмещение. Задачи: а) прямая общего положения преобразуется в прямую уровня; б) прямая уровня преобразуется в проецирующую прямую; в) плоскость общего положения преобразуется в проецирующую плоскость; г) проецирующая плоскость преобразуется в плоскость уровня.

Способ плоскопараллельного перемещения.

С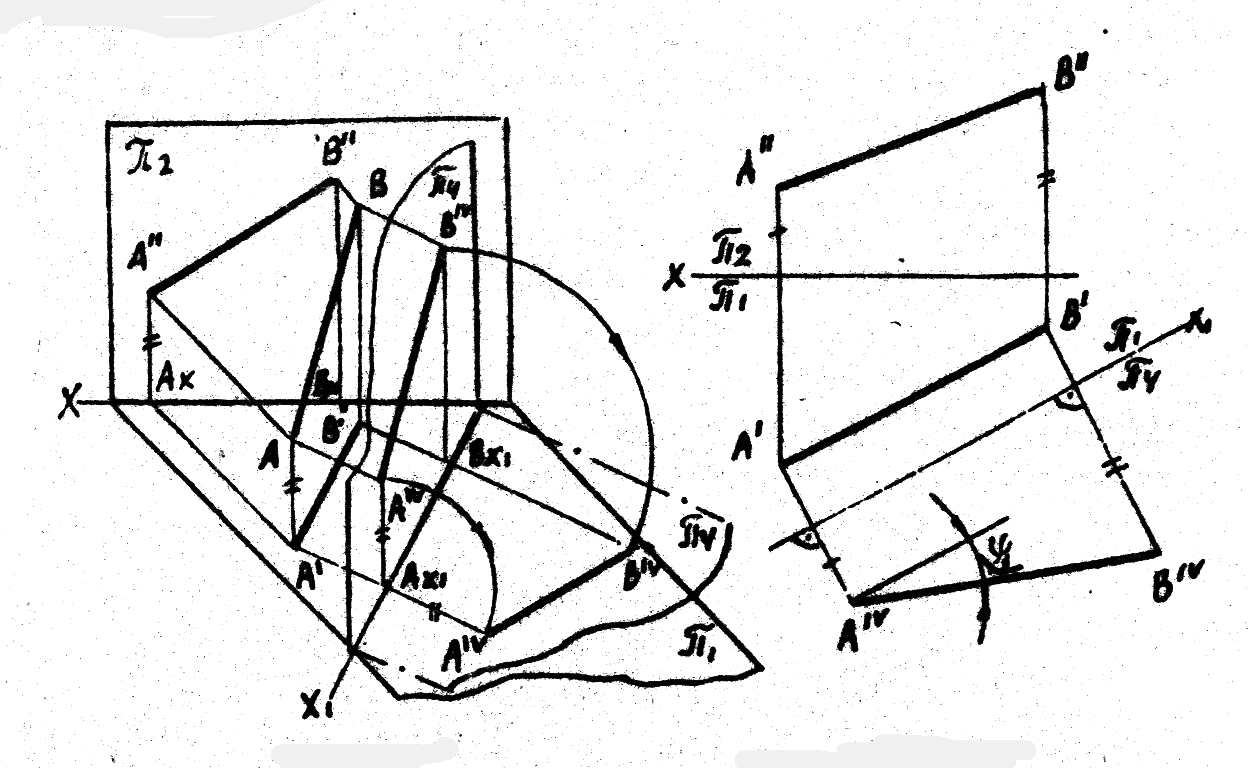 ущность этого способа заключается в перемещении геометрической фигуры относительно данных плоскостей проекций в частное положение таким образом, чтобы траектория перемещения всех ее точек находилась в параллельных плоскостях. Плоскопараллельное перемещение — общий случай вращения без указания местоположения оси. При параллельным переносе геометрической фигуры относительно плоскостей проекций проекция фигуры на эту плоскость хоть и изменяет свое положение, но не изменяется по форме и размерах.