
- •2. Чертеж точки в системе прямоугольных координат. Способы построения недостающих проекций точек.
- •3 . Прямая линия общего и частного положения на эпюре Монжа.
- •4. Следы прямой линии. Сформулировать последовательность построения горизонтального и фронтального следов прямой.
- •5. Определение истинной величины отрезка прямой общего положения способом прямоугольного треугольника.
- •6 . Взаимное положение точки и прямой, двух прямых. Определение видимости проекций точек на скрещивающихся прямых.
- •7. Способы задания плоскостей. Плоскости частного и общего п оложения на эпюре Монжа.
- •8 . Горизонтали и фронтали плоскости. Точка и прямая в плоскости.
- •9. Взаимное положение прямой и плоскости (прямые параллельные и п ерпендикулярные плоскости). Проецирование прямого угла.
- •10. Взаимное положение двух плоскостей. Построение линии пересечения плоскостей при различных способах их задания.
- •1 1. Правила построения точки пересечения прямой с плоскостью. Определение видимости прямой.
- •1 2. Аксонометрические проекции. Основные понятия и определения. Построение окружности в аксонометрических проекциях.
- •1 3. Стандартные виды аксонометрических проекций. Коэффициенты искажения. Построение окружности в аксонометрических проекциях.
- •1 4. Способы преобразования проекций. Способ плоскопараллельного перемещения.
- •1 5. Способ замены плоскостей.
- •16. Способ вращения вокруг проецирующих прямых.
- •1 7. Пересечение многогранников плоскостью частного положения.
- •18. Развертки поверхностей. Развертывание поверхности многогранников.
- •19. Пересечение кривых поверхностей плоскостью частного положения. Линии конических сечений.
- •2 0. Развертывание поверхности прямого кругового конуса и цилиндра.
- •2 1. Цилиндрические и конические винтовые линии. Образование, основные параметры.
- •22. Поверхности. Классификация, определитель и каркасы поверхностей.
- •23. Поверхности вращения. Построение точки на поверхности вращения.
- •2 5. Построение точки пересечения прямой с поверхностью (общий случай). Способы построения точек пересечения прямой с поверхностью.
- •2 6. Построение линии взаимного пересечения многогранных поверхностей.
2. Чертеж точки в системе прямоугольных координат. Способы построения недостающих проекций точек.
Точка в пространстве определяется своими координатами, которые, как правило, имеют числовые значения, например А (x, y, z), А (10, 45, 15). Прямоугольные проекции точки на плоскостях проекций определяются как основания перпендикуляров, опущенных с точки на каждую с плоскостей проекций. Проекции точек обозначаются большими буквами латинского алфавита или числами.
А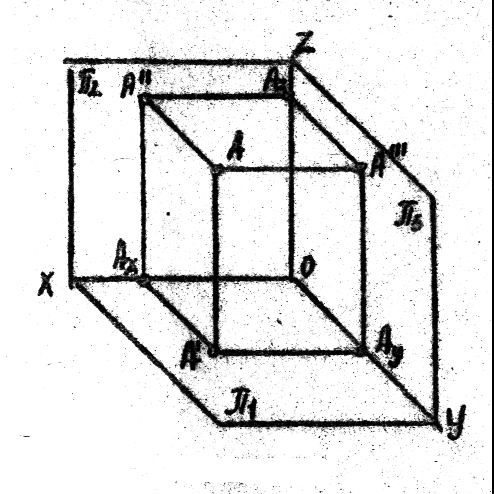 ′ —
горизонтальная
проекция точки
А;
′ —
горизонтальная
проекция точки
А;
А′′ — фронтальная проекция точки А;
А′′′ — профильная поекция точки А.
Д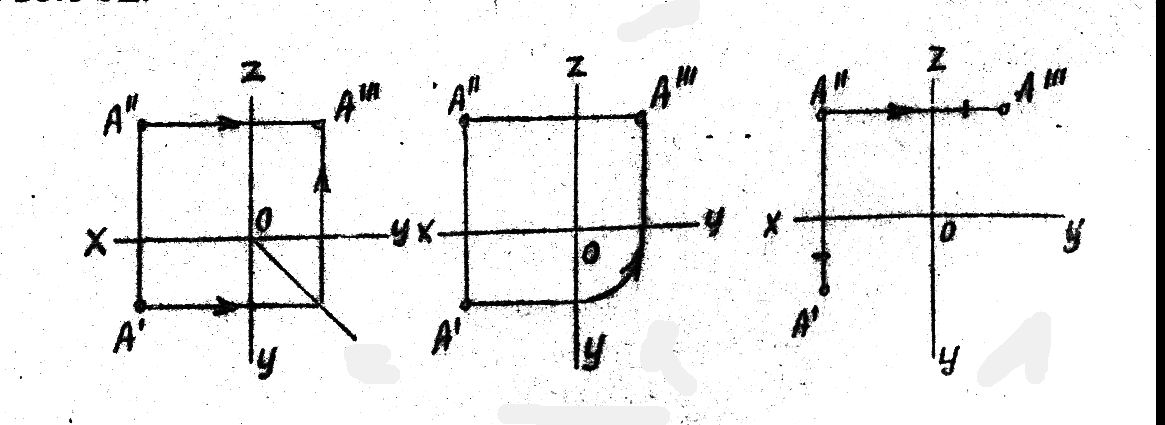 ля
получения проекционного чертежа
совмещают плоскости П1
и П3
с фронтальной плоскостью проекций П2
поворотом соответственно около осей X
и Z.
Тогда на чертеже проекции А′
и А′′ размещаются
на одном перпендикуляре к оси ОX,
а А′′
и
А′′′ — на одном
перпендикуляре к оси ОZ.
Известно три способа построения
профильной проекции точки по данным
двум проекциям.
ля
получения проекционного чертежа
совмещают плоскости П1
и П3
с фронтальной плоскостью проекций П2
поворотом соответственно около осей X
и Z.
Тогда на чертеже проекции А′
и А′′ размещаются
на одном перпендикуляре к оси ОX,
а А′′
и
А′′′ — на одном
перпендикуляре к оси ОZ.
Известно три способа построения
профильной проекции точки по данным
двум проекциям.
3 . Прямая линия общего и частного положения на эпюре Монжа.
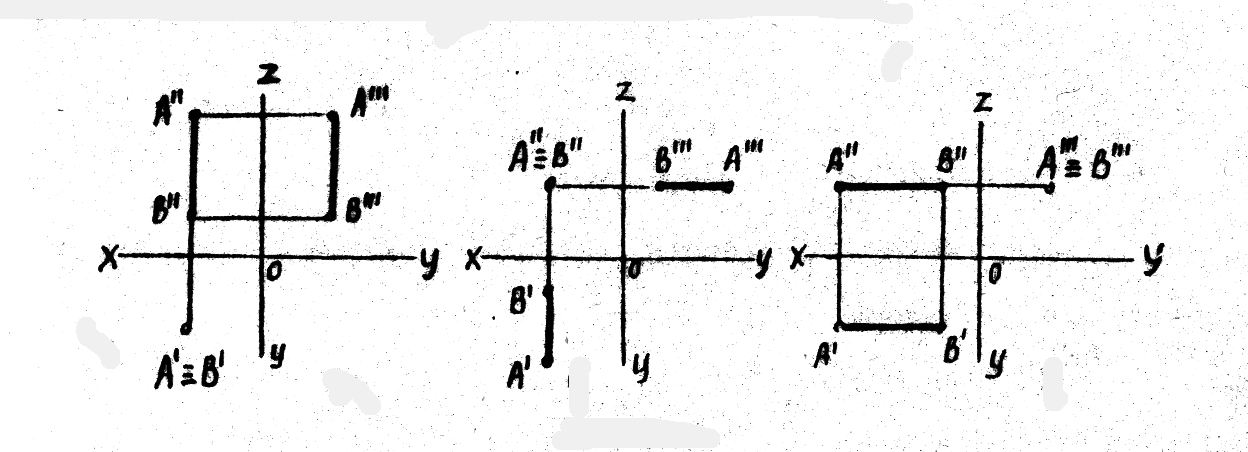
Для того, чтобы выполнить чертеж прямой, необходимо найти проекции двух её точек. В начертательной геометрии, в зависимости от положения прямых относительно плоскостей проекций, они могут иметь свое название — прямые общего и частного положения. Прямая не параллельная ни одной с плоскостей проекций, называется прямой общего положения. Прямые частного положения бывают параллельными или перпендикулярными плоскостям проекций. Прямые, параллельные одной из плоскости проекций, делятся на: горизонтальные прямые — параллельные горизонтальной плоскости проекций; фронтальные прямые — параллельные фронтальной плоскости проекций; профильные прямые — параллельные профильной плоскости проекций. Прямые, перпендикулярные одной из плоскостей проекций, делятся на: горизонтально-проецирующие прямые, перпендикулярные горизонтальной плоскости проекций; фронтально-проецирующие прямые, перпендикулярные фронтальной плоскости проекций; профильно-проецирующие прямые, перпендикулярные профильной плоскости проекций.
4. Следы прямой линии. Сформулировать последовательность построения горизонтального и фронтального следов прямой.
Следом прямой линии называется точка пересечения прямой с соответствующей плоскостью проекций. Для определения горизонтального следа М (М′, М′′) прямой АВ (А′В′, А′′В′′) надо: продлить фронтальную проекцию А′′В′′ до пересечения с осью ОХ (М′′), затем повести перпендикуляр к оси ОХ до пересечения с продолжением горизонтальной проекции А′В′. Для определения фронтального следа N (N′, N′′) прямой надо: продлить горизонтальную проекцию А′В′ до пересечения с осью ОХ, затем провести перпендикуляр к оси ОХ до пересечения с подолжением фронтальной проекции А′′В′′.
М (М′, М′′) — горизонтальный след рпямой АВ (А′В′, А′′В′′);
N (N′, N′′) — фронтальный след прямой АВ (А′В′, А′′В′′).
5. Определение истинной величины отрезка прямой общего положения способом прямоугольного треугольника.
Натуральная величина отрезка прямой общего положения определяется как гипотенуза прямоугольного треугольника, одним катетом которого является проекция отрезка на одну из плоскостей проекций, а второй катет равен разности расстояний концов отрезка до этой же плоскости.
φ1 — угол наклона отрезка АВ к плоскости проекций П1;
φ2 — угол наклона отрезка АВ к плоскости проекций П2.
