Вопрос 2 Учет вклада свободных электронов в теплоемкость.
Теплоёмкость электронного газа — количество теплоты, которую необходимо передать электронному газу для того, чтобы повысить его температуру на 1 К. Она намного меньше по величине при высоких температурах, чем теплоёмкость кристаллической решётки.
Вырожденный газ
Для вырожденного электронного газа в металлах теплоёмкость определяется формулой
,
где
m
*
— эффективная
масса
электронов,
—
приведённая
постоянная Планка,
kB
— постоянная
Больцмана,
μ0
— энергия
уровня
Ферми,
T — температура.
Теплоёмкость стремится к нулю при малых температурах, удовлетворяя теореме Нернста и линейно возрастает с температурой. Поскольку теплоёмкость кристаллической решётки при низких температурах пропорциональная кубу температуры (см. модель Дебая) то существует область низких температур, при которых теплоёмкость электронов больше чем теплоёмкость решётки. Однако при более высоких температурах, чем температура Дебая, вклад электронной подсистемы в общую теплоёмкость твёрдого тела не превышает нескольких процентов. Для этих температур справедливо
,
где
—
теплоёмкость кристаллической решётки.
Объясняется такое соотношение тем, что вклад в электронную теплоёмкость вносят лишь те электроны, которые имеют энергию, близкую к энергии Ферми. Электроны с энергиями, намного низшими чем энергия уровня Ферми, не могут получать тепло, поскольку для увеличения энергии им нужно было бы перейти на близкие энергетические уровне внутри зоны, уже занятые другими электронами. Из-за принципа Паули переход в занятое другим электроном состояние невозможен.
Энергия Фе́рми (EF) системы невзаимодействующих фермионов — это увеличение энергии основного состояния системы при добавлении одной частицы. Это эквивалентно химическому потенциалу системы в ее основном состоянии при абсолютном нуле температур. Энергия Ферми может также интерпретироваться как максимальная энергия фермиона в основном состоянии при абсолютном нуле температур. Энергия Ферми — одно из центральных понятий физики твёрдого тела.
Физический смысл уровня Ферми: вероятность обнаружения частицы на уровне Ферми составляет 0,5 при любых температурах.
Билет 4
Вопрос 1 Распределение электронов по энергетическим зонам в металлах, полупроводниках и диэлектриках.
Согласно постулатам Бора, в изолированном атоме энергия электрона может принимать строго дискретные значения (также говорят, что электрон находится на одной из орбиталей).
В случае нескольких атомов, объединенных химической связью (например, в молекуле), электронные орбитали расщепляются в количестве, пропорциональном числу атомов, образуя так называемые молекулярные орбитали. При дальнейшем увеличении системы до макроскопического кристалла (число атомов более 1020), количество орбиталей становится очень большим, а разница энергий электронов, находящихся на соседних орбиталях, соответственно очень маленькой, энергетические уровни расщепляются до практически непрерывных дискретных наборов — энергетических зон. Наивысшая из разрешённых энергетических зон в полупроводниках и диэлектриках, в которой при температуре 0 К все энергетические состояния заняты электронами, называется валентной зоной, следующая за ней — зоной проводимости. В металлах зоной проводимости называется наивысшая разрешённая зона, в которой находятся электроны при температуре 0 К.
В основе зонной теории лежат следующие главные приближения:
1. Твердое тело представляет собой идеально периодический кристалл.
2.Равновесные положения узлов кристаллической решетки фиксированы, т.е. ядра атомов считаются неподвижными (адиабатическое приближение). Малые колебания атомов вокруг равновесных положений, которые могут быть описаны как фононы, вводятся впоследствии как возмущение электронного энергетического спектра.
3. Многоэлектронная задача сводится к одноэлектронной: воздействие на данный электрон всех остальных описывается некоторым усредненным периодическим полем.
В различных веществах, а также в различных формах одного и того же вещества, энергетические зоны располагаются по-разному. По взаимному расположению этих зон вещества делят на три большие группы (см. Рисунок 1):
проводники — зона проводимости и валентная зона перекрываются, образуя одну зону, называемую зоной проводимости, таким образом, электрон может свободно перемещаться между ними, получив любую допустимо малую энергию. Таким образом, при приложении к твердому телу разности потенциалов, электроны смогут свободно двигаться из точки с меньшим потенциалом в точку с большим, образуя электрический ток. К проводникам относят все металлы.
полупроводники — зоны не перекрываются и расстояние между ними составляет менее 3.5 эВ. Для того, чтобы перевести электрон из валентной зоны в зону проводимости требуется энергия меньшая, чем для диэлектрика, поэтому чистые (собственные, нелегированные) полупроводники слабо пропускают ток.
диэлектрики — зоны не перекрываются и расстояние между ними составляет более 3.5 эВ. Таким образом, для того, чтобы перевести электрон из валентной зоны в зону проводимости требуется значительная энергия, поэтому диэлектрики ток практически не проводят.
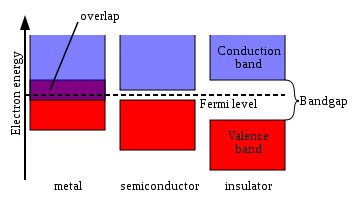
Рис.1