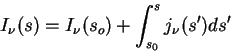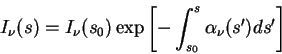- •Вопрос 1 Явление переноса в газах: диффузия, теплопроводность, вязкость
- •Вопрос 2 Теория теплоёмкости Эйнштейна
- •Недостатки теории
- •Вопрос 1Пространственная решетка. Элементарная и примитивная решетки.
- •Вопрос 2 Уравнение Аррениуса
- •Вопрос 1 Природа пластичности твердых тел
- •Вопрос 2 Учет вклада свободных электронов в теплоемкость.
- •Вырожденный газ
- •Вопрос 1 Распределение электронов по энергетическим зонам в металлах, полупроводниках и диэлектриках.
- •Вопрос 2 Понятие длинны и времени выравнивания концентрации в газах и времени выравнивания температуры.
- •Вопрос 1Пространственные группы и кристаллические классы
- •Вопрос 2 Перемещение атомов в твёрдых телах на большие расстояния.
- •Вопрос 1 Дефекты кристаллической решётки.
- •Вопрос 2 Теория теплоёмкости Дебая.
- •Вопрос 1 Общее уравнение переноса
- •Вопрос 2 Решетка с базисом на примере кубической объемно центрированной и кубической гранецентрированной решеток. Простая, объемно- и гранецентрированная кубические решетки
- •Вопрос 1 Квантовая теория электропроводности металлов
- •Вопрос 2 Эффект Холла как метод исследования полупроводников
- •Вопрос 1 Поглощение света в кристаллах
- •Вопрос 2 Закон Видельмана- Франса
- •Вопрос 1Частные случаи общего уравнения переноса
- •Процесс переноса массы
- •Процесс переноса энергии
- •Вопрос 2 Нормальные колебания решетки
- •Вопрос 1 Сравнение механизма электропроводности металлов с механизмов проводимости в полупроводниках
- •Вопрос 2 Теплопроводность твердых тех
- •Вопрос 1 Понятие о симметрии кристаллической решетки
- •Вопрос 2 вакансионный механизм диффузии в твердых телах
- •Вопрос 1 Теплоемкость твердых тел
- •Вопрос 2 Эффект Холла в полупроводниках конечных размеров
- •Вопрос 1 Зависимость концентрации свободных электронов их подвижности и проводимости от температуры
- •Вопрос 2 Используем статистику Ферми-Дирака для описания электронного газа в полупроводнике.
- •Вопрос 1 Электропроводность чистых металлов. Правило Маттисена
- •Вопрос 2
- •Вопрос 1 Понятие эффективного диаметра молекул их длины свободного пробега
- •Вопрос 2 Определение энергии Ферми
- •Вопрос 1 Эффект Холла в неограниченном веществе
- •Вопрос 2 Индексы Милера
- •Вопрос 1 Модель свободных электронов
- •Вопрос 2 Методы изучения структуры твёрдых тел с помощью рентгеновского излучения.
- •Вопрос 1 Понятие о фононах
- •Вопрос 2 Зависимость концентрации, подвижности и проводимости полупроводников от температуры
- •Вопрос 1 Теплопроводность металлов
- •Вопрос 2 определение ширины запрещенной зоны полупроводников оптическим методом
- •Вопрос 1 Квантовая теория электропроводности
- •Вопрос 2 Атомный механизм диффузии в междоузлии
- •Вопрос 1 Сравнение классической теории электропроводности с квантовой
- •Вопрос 2 Оптика полупроводников
- •Вопрос 1 Условия выбора элементарных ячеек по Браве
- •Вопрос 2 Теория теплоемкости Дебая
- •Вопрос 1 Энергия активации диффузии в твердых телах
- •Вопрос 2 учебник Савельев страница 182, 202 (учебник у Славы )
- •Вопрос 1 Частные случаи общего уравнения переноса.
- •Вопрос 2 Связь подвижности электронов со временем релаксации.
- •Вопрос 1 Пространственные группы и кристаллические классы.
- •Вопрос 1 Учет вклада свободных электронов в теплоемкость.
- •Вопрос 2 Симметрия Кристаллов
- •Вопрос 1 Классификация твёрдых тел
- •Вопрос 2 Зависимость сопротивления проводника от температуры
- •Вопрос 2 Оптика полупроводников
- •Вопрос 1 Частный случай общего уравнения переноса: диффузия
- •Вопрос 2 Кубическая сингания
- •Вопрос 1
- •Вопрос 2 Теория теплоёмкости Эйнштейна. Общие положения.
- •Вопрос 1 Связь межплоскостных расстояний с индексами
- •Вопрос 2 Проводимость примесных полупроводников.
Вопрос 2 Теория теплоемкости Дебая
2) В термодинамике и физике твёрдого тела модель Дебая — метод, развитый Дебаем в 1912 г. для оценки фононного вклада в теплоёмкость твёрдых тел. Модель Дебая рассматривает колебания кристаллической решётки как газ квазичастиц — фононов. Эта модель правильно предсказывает теплоёмкость при низких температурах, которая пропорциональна T3. В пределе высоких температур теплоёмкость стремится к 3R, согласно закону Дюлонга — Пти. (закон T 3 страница 165 савельев
При
тепловом равновесии энергия E набора
осцилляторов с различными частотами
![]() равна
сумме их энергий:
равна
сумме их энергий:
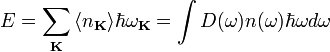
где D(ω) — число мод нормальных колебаний на единицу длины интервала частот, n(ω) — количество осцилляторов в твёрдом теле, колеблющихся с частотой ω.
Функция плотности D(ω) в трёхмерном случае имеет вид:
![]()
где V — объём твёрдого тела, v — скорость звука в нём.
Значение квантовых чисел вычисляются по формуле Планка:
![]()
Тогда энергия запишется в виде
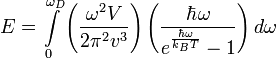
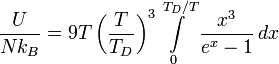
где TD — температура Дебая, N — число атомов в твёрдом теле, kB — постоянная Больцмана.
Дифференцируя внутреннюю энергию по температуре получим:
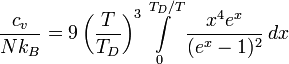
Билет 24
Вопрос 1 Энергия активации диффузии в твердых телах
Зависимость коэффициента диффузии от температуры в простейшем случае выражается законом Арениуса:
D = D0exp( − Ea / kT),
где D — коэффициент диффузии [ {м²}/{сек} ]; Ea — энергия активации [Дж]; k — постоянная Больцмана; T — температура [K].
Вопрос 2 учебник Савельев страница 182, 202 (учебник у Славы )
Билет 25
Вопрос 1 Частные случаи общего уравнения переноса.
Уравнение
переноса Если среда способна как
излучать, так и поглощать свет, то,
полагая коэффициенты излучения
![]() и
поглощения
и
поглощения
![]() известными
функциями координат и времени, зависящими
от физического состояния вещества
(температуры, плотности, химического
состава и т.д.), в стационарном случае
можем записать
известными
функциями координат и времени, зависящими
от физического состояния вещества
(температуры, плотности, химического
состава и т.д.), в стационарном случае
можем записать
|
(*) |
Замечание 1. Фотоны из пучка могут исчезать не только из-за истинного поглощения, но и из-за рассеяния (во многих реальных условиях, например, в солнечной короне, преобладает рассеяние на свободных электронах). Тогда ситуация значительно усложняется, поскольку рассеяние изменяет траектории фотонов, и уравнение переноса превращается в интегро-дифференциальное уравнение, которое решается, как правило, численными методами.
Замечание 2. Простейшие частные случаи уравнения переноса (*)
1.
Пусть среда только излучает,
![]() ,
,
![]() ,
,
|
|
2.
Пусть среда только поглощает,
![]() ,
,
![]()
|
|
Вопрос 2 Связь подвижности электронов со временем релаксации.
Подвижность носителей заряда — коэффициент пропорциональности между дрейфовой скоростью носителей и приложенным внешним электрическим полем. Определяет способность электронов и дырок в металлах и полупроводниках реагировать на внешнее воздействие.
Размерность подвижности м2/(В·с) или см2/(В·с).
Подвижностью
носителей заряда
 называется дрейфовая скорость носителей
заряда, которую они приобретают в
электрическом поле с напряженностью 1
В/м.
называется дрейфовая скорость носителей
заряда, которую они приобретают в
электрическом поле с напряженностью 1
В/м.
Очевидно,
что если носители заряда движутся в
поле с напря-женностью
 ,
то их дрейфовая скорость:
,
то их дрейфовая скорость:
 .
.
Если
концентрация носителей заряда –
,
заряд –
 ,
то плот-ность электрического тока через
образец равна
,
то плот-ность электрического тока через
образец равна
 .
(1)
.
(1)
По закону Ома
 ,
(2)
,
(2)
где
 – удельная электропроводность вещества
(проводимость), которая согласно (1) и
(2) выражается через подвижность форму-лой:
– удельная электропроводность вещества
(проводимость), которая согласно (1) и
(2) выражается через подвижность форму-лой:

Билет 26