Вопрос 1 Зависимость концентрации свободных электронов их подвижности и проводимости от температуры

Проводимость полупроводников сильно зависит от температуры.

 С ростом температуры число свободных электронов и дырок увеличивается, поэтому в полупроводнике, не содержащем примесей, удельное сопротивление уменьшается. Условно принято считать полупроводниками элементы с энергией связи электронов меньшей чем 1,5—2 эВ. Электронно-дырочный механизм проводимости проявляется у собственных (то есть без примесей) полупроводников. Он называется собственной электрической проводимостью полупроводников. Подвижностью μ называют коэффициент пропорциональности между дрейфовой скоростью   носителей тока и величиной приложенного электрического поля  . Подвижность электронов и дырок зависит от их концентрации в полупроводнике (см. рисунок). При большой концентрации носителей заряда,вероятность столкновения между ними вырастает, что приводит к уменьшению подвижности и проводимости.

Вопрос 2 Используем статистику Ферми-Дирака для описания электронного газа в полупроводнике.

Зонная диаграмма собственного полупроводника приведена на

рис.4. Для того, чтобы получить для собственного полупроводника формулы

аналогичные формулам (6) - (9) надо учесть, что плотность состояний в зоне

проводимости Z(E) ( а именно она нас интересует) фактически определяется

выражением (6) с учетом того, что уровнем для начала отсчета энергий должен

быть выбран уровень Е_пр, соответствующий дну зоны проводимости.

Билет 15

Вопрос 1 Электропроводность чистых металлов. Правило Маттисена

Электропроводность чистых металлов описывается соотношением (103).

Так как концентрация электронов проводимости в чистых металлах не

зависит от температуры, то изменение σ(T) определяется исключительно

изменением подвижности U(T).

Для области высоких температур:

σ =С/Т (109)

ρ= α Т (110)

где σ - электропроводность, ρ ; - удельное сопротивление, С и α -

коэффициенты пропорциональности.

Для области низких температур: 71

σ =В/Т(Т в пятой степени) (111)

ρ = βТ(Т в пятой степени) (112)

где B, β -коэффициенты пропорциональности.

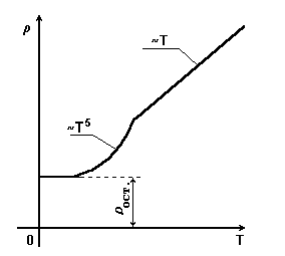
На рисунке 3.2 показана схематическая кривая зависимости удельного

сопротивления чистых металлов от температуры. В области высоких

температур графиком (T) является прямая, в области низких температур -

парабола 5-й степени, и вблизи абсолютного нуля, где основное значение

приобретает рассеяние на примесях - прямая, идущая параллельно оси

температур.

Рисунок 3.2. Зависимость удельного сопротивления чистых металлов от

температуры

Правило Матиссена (Matthiessen's rule).

    Если имеется несколько механизмов рассеяния, каждый из которых не влияет на другие, то полная вероятность рассеяния

W =  iWi.

(10.1)

  В приближении времени релаксации:

1/  =   i 1/ i.

(10.2)

Предположим, кроме того, что время релаксации для каждого механизма не зависит от k. Тогда

= m/(ne2 ) = m/(ne2)  i 1/ i =   i i .

(10.3)

Это т.н. правило Матиссена: удельное сопротивление = сумме парциальных удельных сопротивлений, обусловленных каждым механизмом. Ограниченность этого правила связана с предположениями а) о независимости механизмов, б)  (k) = const. Можно показать, что правило Матиссена выполняется как неравенство:

>  i  i.

1. Теплопроводность, обусловленная атомными колебаниями (решёточная теплопроводность)

Решеточная теплопроводность твердого тела, как и теплоемкость, обусловлена тепловыми колебаниями атомов, амплитуда которых, определяющая внутреннюю энергию решетки, увеличивается с ростом температуры. Благодаря сильной связи между атомами тепловое возбуждение, возникшее в каком-либо месте решетки, передается от атома к атому в виде упругой волны, приводя их в коллективное движение, подобное распространению звуковых волн в твердом теле. Достигая поверхности тела, упругая волна отражается от нее. Наложение прямой и отраженной волн приводит к установлению в решетке стоячей волны с частотой, которая называется нормальным колебанием. Всего в теле с Nатомами можно возбудить 3N нормальных колебаний с собственными дискретными частотами _I, которые упрощенно удовлетворяют тому условию, что на поверхности тела должны располагаться узлы стоячей волны (в узлах амплитуда колебаний равна нулю), а между узлами укладываться целое число полуволн   т.е. _i  , где U  скорость звука в теле.

Максимальная частота нормальных колебаний не может превышать

2. _max   

где d – расстояние между соседними атомами. Физически это означает, что не может наблюдаться колебание с длиной волны, меньшей удвоенного расстояния между атомами (см. рис. 1). Минимальная частота колебаний _min ограничивается линейными размерами кристалла L,

_min   .