Процесс переноса массы

Процесс переноса массы обусловливает явление диффу-зии. Диффузия – это самопроизвольное выравнивание кон-центраций в смеси нескольких различных веществ. Такое выравнивание концентраций происходит из-за теплового хаотического движения молекул. Рассмотрим смесь двух га-зов при постоянной температуре и давлении во всем объеме сосуда. При этих условиях не будет газодинамических по-токов, взаимопроникновение молекул будет обусловлено только тепловым движением. Суммарная концентрация 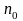обеих компонент не изменяется в зависимости от коорди-наты по оси . От координаты зависят концентрации обеих смесе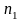й ( и 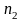). То есть возникает градиент концен-трации одной из компонент, что служит причиной возник-новения процесса переноса массы каждой компоненты в на-правлении уменьшения ее концентрации (рис. 2.2).

Переносимой величиной будет являться концентрация молекул одной из компонент:

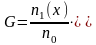(2.3)

Получаем выражения для потока этой величины:

(2.4)

В случае, когда смесь состоит из большего количества компонент, поток 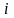-й компоненты будет выражаться тем же соотношением:

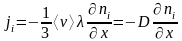, (2.5)

где

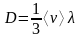(2.6)

– коэффициент диффузии.

Мы получили выражение для потока через единичную площадку. При определении потока через площадку , по-лучаем соотношение, описывающее поток молекул -й ком-поненты:

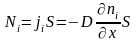. (2.7)

Из этого соотношения можем получить выражение для потока массы -й компоненты. Для этого умножим обе части уравнения на массу 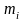молекулы -й компоненты:

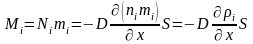, (2.8)

где 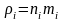– парциальная плотность -й компоненты.

Два последних выражения (2.7) и (2.8) были получены эмпирическим путем и носят название закона Фика.

Размерность коэффициента диффузии – 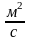. Коэффициент диффузии определяет массу, переносимую через поверх-ность площадью 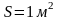за 1 секунду при градиенте плот-ности, равном 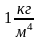. Коэффициент диффузии приближенно обратно пропорционален давлению, а при постоянном дав-лении пропорционален .

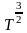Процесс переноса энергии

Это процесс лежит в основе явления теплопроводности. Если в некоторой среде возникает градиент температуры, то возникает поток тепла. В этом случае переносимой вели-чиной будет средняя кинетическая энергия теплового дви-жения одной молекулы 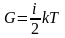. Плотность потока тепла составит

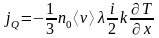. (2.14)

Переносимую величину представим в виде:

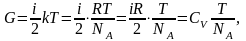(2.15)

где – молярная теплоемкость при постоянном объеме. Отсюда получаем

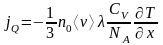. (2.16)

Умножив и разделив на массу молекулы, и учтя, что 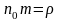– плотность вещества и 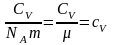– удельная теплоемкость вещества, получаем выражение для теплового потока через единичную площадь:

где

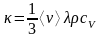(2.18)

– коэффициент теплопроводности.

Окончательно,

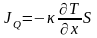. (2.19)

Полученное соотношение называется законом Фурье. Теплопроводность не зависит от давления и пропорцио-нальна .

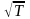Коэффициент теплопроводности может быть получен из коэффициентов диффузии и вязкости:

.

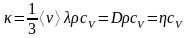Коэффициент теплопроводности имеет размерность 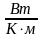и численно равен энергии, переносимой в виде теплоты за 1 секунду через плоскую поверхность площадью при градиенте температуры, равном единице.

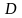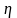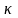Общими свойствами всех трёх коэффициентов является то, что эмпирически определив , и , мы можем вы-числить длину свободного пробега и эффективный диа-метр молекул .
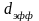