20. Избирательное смачива­ние. Способы определения краевого угла смачивания. Инверсия смачиваемости поверхности.

п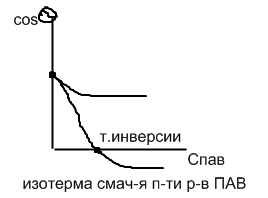 ри нанесении на пов-ть 2х жид нерастворимых друг в друге, мужду ними образ краевой угол, характеризующий относ. спос-ть этих жидкостей смач-ть данное тело. Для срав­нительной оценки смачивания поверхности,сопоставление проводят по сравнению с водой (с полярынми жид-ми) Инверсия: заключается в качеств-м из­мен-и смач-ти пов-ти за счет адсобции ПАВ. Избирательное смач-е: добыча нефти, офсетная печать, изгот-е пиг­ментов для масл.красок.

21. Молекулярно-кинитиче­ские свойства дисперсных систем: броуновское движе­ние, диффузия. Броуновское движение проявляется в хао­тическом движении частиц дисперсной фазы под дейст­вием ударов молекул раство­рителя, находящихся в состоя­нии интенсивного молеку­лярно-теплового движения. Колич.мера передвижения частиц – смещение или сдвигом час­тицы называется расстояние между проекциями начальной и конечной точек траектории на оси смещения. Диффузия – это процесс самопроизволь­ного выравнивания концен­трац. В сис-ме, приводящий к установлению равенства хим. Потенциала во всех точках системы. Движу­щая сила - бро­уновское движе­ние.Количественная хар-ка диффу­зии-диффузионый поток-это колво моль веще­ства,переносимого диффузи­ей за ед.времени через ед.пло­щади поверхностити.

Закон Фика [D]=м2\с , ,

22. Седиментация суспензий и седиментационный анализ дисперсных систем.

Процесс оседания частиц дис­персной фазы в жидкой или газовой дисперсионной среде под действием силы тяжести есть седиментация суспензий . По мере увеличения ск-ти осе­дания возникает сила трения пропор. Ск-ти час­тицы.F_тр=BU. Частица дви­жется с постоянной скоро­стью, если сила трения урав­новешена силой тяжести. V=2g(p-p₀)r²/9η-закон седи­ментации, условия соблюде­ния данного закона: 1)Независимость оседания частиц(разб.системы) 2)Ламинарность 3) Дисперсность r=10^-7/10^-5

4) Сферическая форма частиц. Седиментационный анализ ос­нован на различных скоростях оседания частиц разного раз­мера, с помощью его можно найти средний радиус час­тицы, описывается ур-ями: m=(Q/H)*Uτ, где Q-общая масса, H-первоначальная вы­сота столба суспензнии m=2Q_д(p-p₀)r²τ/9ηH, а также уравнением Сведберга-Одена m=q_i+(dm/dτ)τ СМОТРЕТЬ ГРАФИК ТЕМА 3.5!!! Диффе­ренциальные кривые распре­деления показывают распреде­ление масс частиц по их раз­мерам,а функция распределе­ния представляет собой долю частиц в интервале(r+dr)

23. Седиментационно-диффу­зионное равновесие. Седимен­тационная устойчивость.

, , где -плотность частицы, - плот­ность дисп.среды, концентрация частич у дна сосуда, когда h=0, -концентрация частиц на вы­соте h от дна сосуда, V-объем частицы. Седим.устойчивость- способность системы протои­востоять действию силы тяже­сти. Чем больше размеры час­тицы,тем быстрее скорости оседания частиц.

24. реологические свойства дисперсных систем. Понятия об упругих,вязких и пласти­ческих деформациях. Реоло­гия – наука о деформации и течении материала. Совокуп­ность механических свойств – прочность, упругость, эла­стичность, пластичность – яв­ляется важной характеристи­кой материала. Поскольку эти свойства связаны со структу­рой, они называются струк­турно –механическими. Упру­гопластические свойства ха­рактеризуют способность тел сопротивляться деформациям. Существуют два основных вида деформации: растяжение или сжатие и сдвиг. Деформа­ции бывают упругими – тело полностью восстанавливает свои свойства после снятия нагрузки- и остаточные – без разрушения, возникает под действием тангенциального напряжения. В соответствии с этим тела делятся на упругие и пластичные. Деформации уп­ругих тел описываются зако­ном Гука : P=Е γ. Е – модуль Юнга характеризует жесткость тела. При напряжении боль­шем критического происходит либо разрушение, либо оста­точные деформации, харак­терные для пластичных тел. В этом случае устанавливается течение с постоянной скоро­стью при постоянном напря­жении, отвечающем пределу текучести ( прочности). Вязкие тела отличаются от пластиче­ских тем, что текут при любых напряжениях. Течение иде­ально вязких тел описывается законом Ньютона.

P=ηdU/dx.

В основе пластических дефор­маций – необратимые переме­щения атомов на значительные расстояния от исходных поло­жений равновесия. Закон тече­ния в области разрушения структуры описывается урав­нением Бингама.

25. Основные законы реоло­гии. Классификация дис­персных систем по структуре и структурно-механическим свойствам.Все реальные тела принято делить на жидкооб­разные, текущие при любых напряжениях, и твердообраз­ные. Жидкообразные тела классифицируют на:

1. ньютоновские жидкости – системы, течение которых подчиняется закону Ньютона:

P = ŋ , P – напряжение сдвига, ŋ- коэффициент вязко­сти, - градиент скорости. неньютоновские жидкости – их вязкость зависит как от T, так и от напряжения сдвига. Они подразделяются а стацио­нарные, реологические свой­ства которых не изменяются со временем, и нестационар­ные, для которых эти характе­ристики зависят от времени. Наиболее общим уравнением, описывающим течение ста­ционарных неньютоновских жидкостей, является эмпири­ческое уравнение Оствальда-Вейля: , где k и n – постоянные, данную жидко­образную систему. Если n=1, жидкость является ньютонов­ской, и константа k совпадает с ньютоновской вязкостью ŋ. При n<1 вязкость растет с уве­личением скорости сдвига и напряжения. Эти жидкости наз-ся дилатантными.

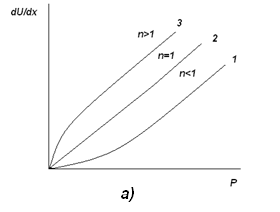
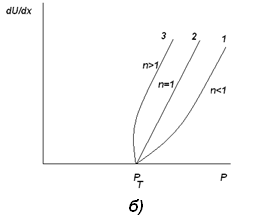
а-для жидкообразных тел, б-для твердообразных

Разбавленные грегативно-ус­тойчивые ДС со сферическими частицами обычно представ­ляют собой ньютоновские ж-ти.

ур-е Эйнштейна: ŋ= ŋ₀(1+α φ) α-коэффициент формы час­тицы

φ-объемная концентрация дисп.фазы

Согласно теории структуриро­вания все структуры в колло­идных системах делаятся на: -коагуляционные (за счет ван-дер-ваальсовых сил притяже­ния частиц) -конденсационно-кристализа­ционные(хим взаимодействие между частицами и их сраста­ние)